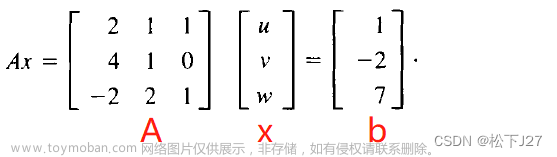
看过我前几个博文的小伙伴们,细心的小伙伴会发现我前面讲过一个高斯消元法,那么和接下来讲的列主高斯消去法有什么区别呢??
目录
一、前言
二、列主高斯消元法
1.数学计算过程
三、代码实现过程
1、源代码展示(这次没有采用高斯消元法中校园的时候,进阶的列表表达式,相对于上次,这次比较好理解)
在写代码中需要注意的问题:
四、总结
这一期的分享就到次结束了(写了两个中午,开始学数值分析是真的难),下面我将继续更新数值分析这本书上的所有算法,谢谢大家!!!
一、前言
在高斯消元法过程中,回代的过程是将主对角线上的主元作为除数(这个也是将主元作为除数的),但是一旦遇到主元上的数非常的小,即小主元。由误差分析的知识得,如果将小的数字作为除数,那就会带来误差,因此为了避免误差应当避免小主元做除数。所以我们引入了列主高斯消去法。
二、列主高斯消元法
1.数学计算过程
下面是我求解的线性方程组,然后我将其已经转化为增广矩阵(A,b),接下来将要对增广矩阵进行消元达到上三角矩阵的格式,在列主消元的过程中(顾名思义我们是按照列进行消元的,也就是说我们在进行消元的过程中是一列一列进行消元的,认识到这一点非常重要,因为这时我们就要将最外层的循环按列进行遍历,后面我还会将行主消元法和全主消元法)。
1)增广矩阵

2)将第1列上面的所有元素绝对值分别与第1行主对角线上的元素的绝对值作比较,将绝对值大的元素相对应的行与第1行交换位置;得到下面结果:

3)用第一行元素值消去第一行主对角线上下面的两个元素值;得到下面结果:

4)将第2列上面的所有元素绝对值(此时已经不考虑第一行的元素值了)分别与第2行主对角线上的元素的绝对值作比较,将绝对值大的元素相对应的行与第2行交换位置;得到下面结果:

5)用第二行元素值消去第一行主对角线上下面的两个元素值;得到下面结果:

6)将第3列上面的所有元素绝对值(此时已经不考虑第一、二行的元素值了)分别与第3行主对角线上的元素的绝对值作比较,将绝对值大的元素相对应的行与第3行交换位置;得到下面结果:

三、代码实现过程
我们只需要在高斯消元法的基础上做一些修改即可,主要是在消元的过程中,回代过程不需要修改。
1、源代码展示(这次没有采用高斯消元法中校园的时候,进阶的列表表达式,相对于上次,这次比较好理解)
"""
作者:author
日期:2022年09月19日
"""
import numpy as np
t=[]
s = np.zeros((3,4))
m = ([[2.0,3.0,-3.0,5.0],
[4.0,2.0,-1.0,7.0],
[1.0,4.0,0.0,9.0]])
def exchange_large(m,col):#
for i in range (col+1,len(m)):
if (abs(m[col][col])<abs(m[i][col])):
t[:] = m[col]
m[col] = m[i]
m[i] = t[:]
return m
#先列后行,因此在外层遍历列:从0列 1列 到n-1列
# 当遍历到0列时,需要遍历1,2,……,再到最后一行,就是不用遍第一列,因为此时恰好col的下标为0,表示第一列,并且也可以表示第一行; # 当遍历到1列时,需要遍历2,3,……,再到最后一行,就是遍历前两列,因为消去第二个主元下面的元素只需用到第二列来消去,恰好col的下标为1,并且也可以用来表示第二行。
def myGauss(m):
# 消元过程,比高斯消元法多了个将每一列大的元素值挑选出来并作为主元
for col in range(len(m[0])):#依次遍历0列 1列 2列 3列 4列
m=exchange_large(m, col)
for row in range(col+1,len(m)):#0行对应:1遍历到最后一列; 1行对应:2遍历到最后一列
x=-((m[row][col])/(m[col][col]))#先找出要乘的系数,而且每一次的系数都不一样
for i in range(len(m[0])):#给每一个元素乘以系数
s[col][i]=(m[col][i]*x)
m[row]+=s[col]
#回带过程
ans=[]#初始化一个矩阵
#m = list(m)
m.reverse()
for sol in range(len(m)):
if sol == 0:
ans.append((m[sol])[-1]/m[sol][-2])#倒数第一个数除以倒数第二个数,这是第一行的情况
#ans里面放方程的根
else:
inner = 0#这是第一行下面的情况
#
for x in range(sol):#
inner += (ans[x]*m[sol][-2-x])#将求出的所有解依次乘以其下面的元素
ans.append((m[sol][-1]-inner)/m[sol][-sol-2])#右边的值减去上一个的结果然后除以x的系数(这一行的倒数第三个元素)
ans.reverse()
return ans
print(myGauss(m))在写代码中需要注意的问题:
1.创建临时保存一行数据的临时变量的时候,我们要用到的是t[:],这样就会保存到一行的数据,而不能用t,不然就会报错。
2.s = np.zeros((3,4)),输入这一行代码时,需要注意到,这里有两个“()”括号,输入一个同样也会报错。
3.在写具体的某一行代码时,尽可能多的将自己的注释写上去,这样方便别人的同时,也方便自己下次修改。
4.定一个函数时,这个函数必须要有完整的结构,比如return,如果没有的话,对于本题来说就会报错。
5.最好学会用debug功能,这样很方便就可以查出自己所犯得小问题。文章来源:https://www.toymoban.com/news/detail-814940.html
6.你还遇到过哪些小问题,调试了半天就是找不见,可以在评论区留言。文章来源地址https://www.toymoban.com/news/detail-814940.html
四、总结
这一期的分享就到次结束了(写了两个中午,开始学数值分析是真的难),下面我将继续更新数值分析这本书上的所有算法,谢谢大家!!!
到了这里,关于列主高斯消元法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!