贪心算法-01：跳跃游戏-Toy模板网

这篇具有很好参考价值的文章主要介绍了贪心算法-01：跳跃游戏。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

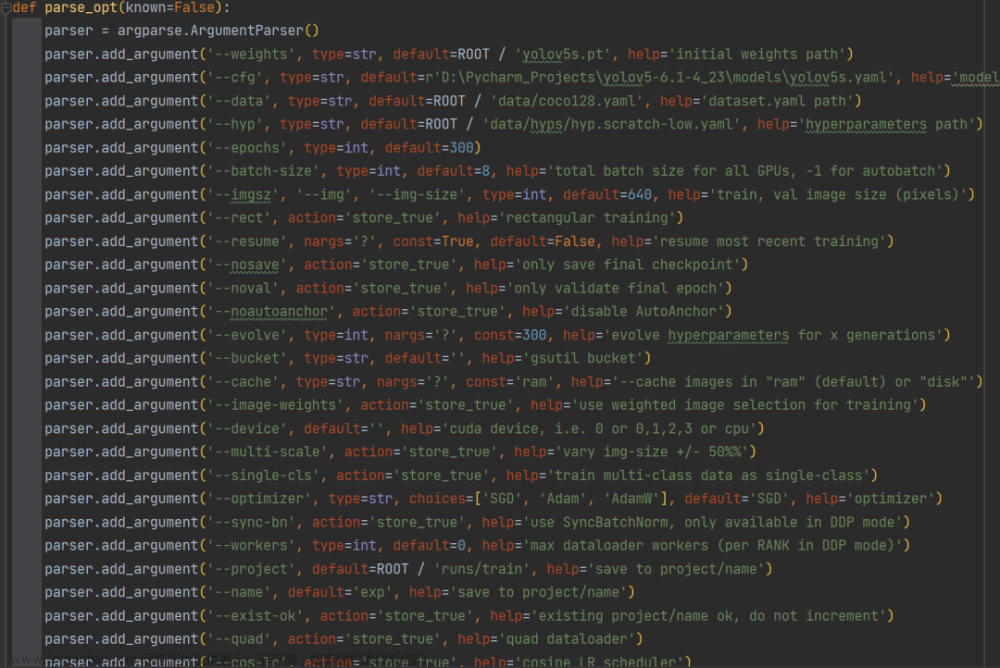
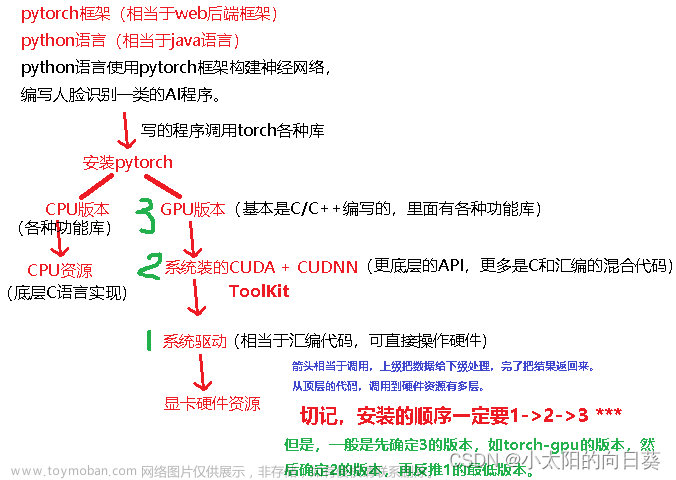
关于贪心算法

贪心算法是动态规划的一个特例，相对于动态规划，使用贪心算法需要满足更多条件，但是效率比动态规划要高。

贪心选择的性质就是：每一步都做出一个局部最优解，最终的结果就是全局最优。不过这是一种特殊性质，只有一部分问题拥有这个性质。

比如面前放有100张人民币，你只能拿十张。想要拿到最高的金额，就需要每次选择剩下钞票中面值最大的一张，最后你的选择一定是最优的。

接下来，我会演示跳跃游戏Ⅱ的动态规划解法和贪心算法解法，通过对比来说明贪心算法的 “局部最优解” 是怎样的。

力扣45.跳跃游戏Ⅱ

贪心算法-01：跳跃游戏,手把手带你刷力扣Hot100,贪心算法,游戏,算法

动态规划解法

定义dp函数

使用动态规划解法就是 [分解问题]。

我们的原始问题是：从初始位置跳到最后一个位置的最小跳跃次数。

我们将其分解出子问题：从索引 p 跳到最后一个位置的最小跳跃次数。

//定义dp函数：从索引p跳到数组末尾的最小跳跃次数为dp(nums,p)
int dp(int[] nums,int p)

base case

对边界问题进行处理。这里的边界问题就是当索引 p 到达数组末尾时，不需要跳跃

if(p >= nums.length - 1){
    return 0;
}

使用备忘录数组解决重叠子问题，写出动态规划解法的代码

public int jump(int[] nums) {
    int n = nums.length;
    //memo[i] 表示从 0 到 i 下标最少跳跃次数 
    int[] memo = new int[n];
    //将数组初始化为一个不可能取到的值，比如 n
    //(因为从 0 到 n-1 最多 n-1 步)
    Arrays.fill(memo, n);
    return dp(nums, 0, memo);
}

public int dp(int[] nums, int p, int[] memo) {
    int n = nums.length;
    //base case
    if (p >= n - 1) {
        return 0;
    }
    if (memo[p] != n) {
        return memo[p];
    }
    //获取索引 p 中的跳跃步数，做为选择列表
    int steps = nums[p];
    for (int i = 1; i <= steps; i++) {
        //写出子问题
        int subProblem = dp(nums, p + i, memo);
        //写出状态转移方程
        memo[p] = Math.min(memo[p], subProblem + 1);
    }
    return memo[p];
}

贪心算法解法

刚才的动态规划思路穷举了所有的子问题，然后取最小的作为结果。而贪心算法并不穷举所有子问题，而是每次做出最优的选择

贪心算法-01：跳跃游戏,手把手带你刷力扣Hot100,贪心算法,游戏,算法

对于这个 0 下标来说，有1、2、3 三种跳法。其中选择跳两步到 2 下标，然后再跳 4 步，能挑到最远距离。所以我们只选择这种情况来遍历，这就是我们的最优解

我们使用 end 来记录：“目前能够到达的最远距离”。以上图为例，当 i = 0 时，我们能够到达的最远距离为 3 下标。

我们使用 farthest 来记录： “以当前下标为起点能够跳到的最远距离”。以上图为例，当 i = 0 时，我们能够到达的最远距离为 3 下标；当 i = 2 时，我们能够到达的最远距离就是 6 下标。

那么我们就要选择能够跳的最远的下标作为我们的最优解。当我们以 0 下标为起点时，“目前能够到达的最远距离” 是 3 下标，所以 end = 3.

我们能够选择的下标中（能选择1、2、3 下标），2下标能跳的最远，最远能跳到 6 下标，farthest = 6。所以我们以 2 下标为目的地进行一次跳跃。

所以我们遍历数组中每一个下标的目的，就是为了找到 “以这个下标为起始点，能够跳到最远距离”，当遍历的下标超出了目前我们能够到达的最远距离，我们进行一次跳跃，并更新 “目前能够到达的最远距离” end

public int jump(int[] nums) {
    int n = nums.length;
    int end = 0, farthest = 0;
    int jumps = 0;
    for (int i = 0; i < n - 1; i++) {
        farthest = Math.max(nums[i] + i, farthest);
        //当下标遍历到我们目前能够到达的最远距离时，进行一次跳跃
        if (end == i) {
            jumps++;
            end = farthest;
        }
    }
    return jumps;
}

力扣55、跳跃游戏

贪心算法-01：跳跃游戏,手把手带你刷力扣Hot100,贪心算法,游戏,算法

这道题比较简单，我们只需要判断跳到的最远距离是否能够超出数组长度即可

class Solution {
    public boolean canJump(int[] nums) {
        int farthest = 0;
        int n = nums.length;
        for(int i = 0;i < n - 1;i++){
            farthest = Math.max(farthest,i+nums[i]);
            if(farthest <= i){
                return false;
            }
        }
        return farthest >= n - 1;
    }
}