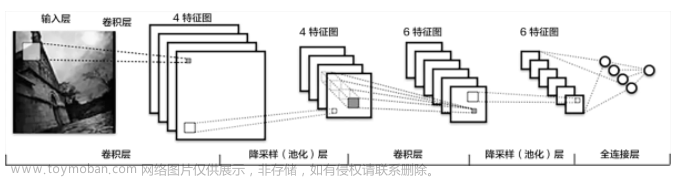
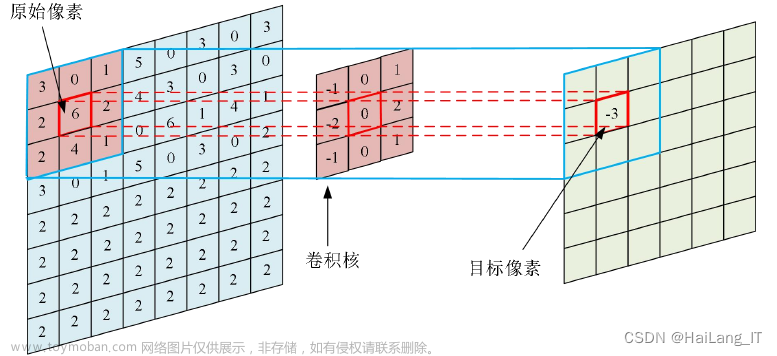
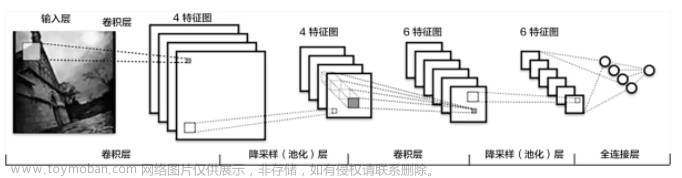
转置卷积(Transposed Convolution)
抽丝剥茧,带你理解转置卷积(反卷积)
目录
一、概念
1、定义
2、运算步骤
二、常见参数
一、概念
1、定义
转置卷积(Transposed Convolution),也被称为反卷积(Deconvolution)或逆卷积(Inverse Convolution),是一种卷积神经网络中常用的操作。转置卷积可以用于图像生成、图像分割、语义分割等任务中。
转置卷积的操作实际上是卷积操作的逆过程。在标准的卷积操作中,输入数据经过卷积核的滑动窗口运算,生成输出特征图。而在转置卷积中,输出特征图经过转置卷积核的滑动窗口运算,生成输入数据的近似重构。
转置卷积的操作可以用矩阵乘法的方式来实现,也可以用卷积的方式来实现。在实际应用中,常常使用卷积的方式来实现转置卷积,而不是直接进行矩阵乘法运算。
转置卷积的计算过程可以简化为以下几个步骤:
- 在输入特征图上进行填充操作,将输入特征图的尺寸扩大一定倍数(根据转置卷积核的大小和步长确定)。
- 将填充后的输入特征图与转置卷积核进行卷积操作,得到中间特征图。
- 对中间特征图进行剪裁操作,使其尺寸与输入特征图相同。
- 得到转置卷积的输出特征图。
通过转置卷积操作,可以将低维的输入特征图扩张为高维的输出特征图,从而实现图像的生成和重构。转置卷积在卷积神经网络中得到广泛应用,如生成对抗网络(GANs)、语义分割网络等。
notes:
- 转置卷积不是卷积的逆运算,只是将特征图大小还原回卷积之前的大小,数值与输入特征层的数值不相同
- 转置卷积也是卷积
- 转置卷积的作用是上采样
2、运算步骤
转置卷积运算步骤:
- 在输入特征图元素间填充行、列0
- 在输入特征图四周填充行、列0
- 将卷积核参数上下、左右翻转
- 做正常卷积运算(填充0,步距1)
![[SS]语义分割_转置卷积,语义分割,人工智能,深度学习,计算机视觉](https://imgs.yssmx.com/Uploads/2024/01/815473-1.png)
输入的特征图大小为2x2(假设输入输出都为单通道),通过转置卷积后得到4x4大小的特征图。这里使用的转置卷积核大小为k=3,stride=1,padding=0的情况(忽略偏执bias)。
![[SS]语义分割_转置卷积,语义分割,人工智能,深度学习,计算机视觉](https://imgs.yssmx.com/Uploads/2024/01/815473-2.png)
notes:
做正常卷积运算中的步距与第一步中的参数s不一样,参数s对应的是转置卷积中的参数s,即输入的特征图是经过步距为s、padding为p,卷积核大小为k的卷积之后得到的。
二、常见参数
torch.nn.ConvTranspose2d参数
文章来源:https://www.toymoban.com/news/detail-815473.html
文章来源地址https://www.toymoban.com/news/detail-815473.html
- in_channels(int)-输入特征图通道数
- out_channels(int)-输出特征图通道数
- kernel_size(int or tuple)-卷积核大小
- stride(int or tuple,optional)-步距大小
- padding(int or tuple,optional)-填充
- output_padding(int or tuple,optional)-输出填充,通常默认为0
- groups(int,optional)-是否采用主卷积,默认为1
- bias(bool,optional)-偏置,默认为True
- dilation(int or tuple,optional)-是否使用膨胀卷积或空洞卷积,默认为1
到了这里,关于[SS]语义分割_转置卷积的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!