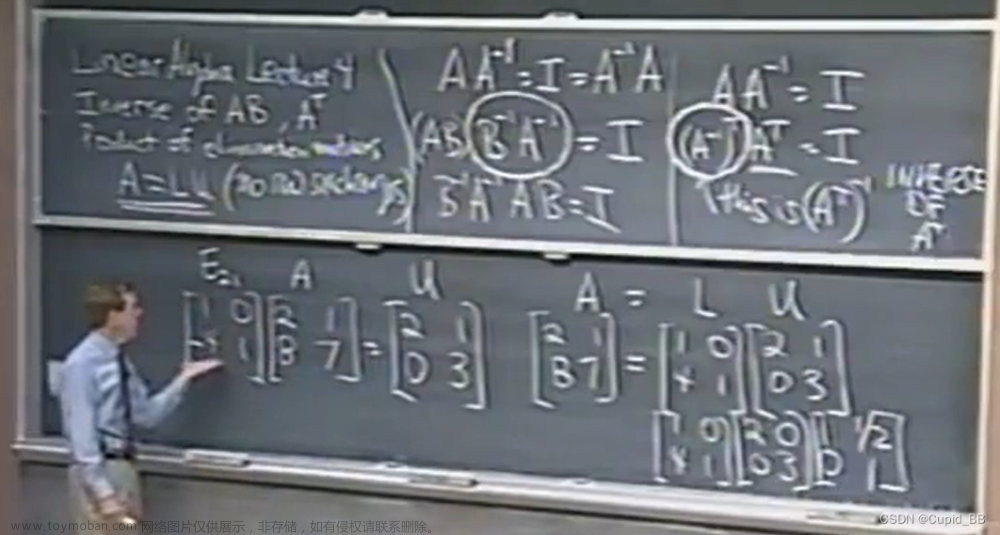【矩阵分析】线性空间、λ矩阵、内积空间、Hermite矩阵、矩阵分解、矩阵范数、矩阵函数-Toy模板网

这篇具有很好参考价值的文章主要介绍了【矩阵分析】线性空间、λ矩阵、内积空间、Hermite矩阵、矩阵分解、矩阵范数、矩阵函数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

单纯矩阵：A可对角化⇔①A可对角化；⇔②n个线性无关的特征向量； ⇔③每个特征值的几何重复度等于代数重复度；⇔④特征值λi对应的pi = n - rank(λiE - A)。
等价矩阵：A(λ)等价于B(λ)⇔① 任意k阶行列式因子相同Dk(λ)；⇔②有相同的不变因子dk(λ)；⇔③相同的初等因子，且秩相等。
相似矩阵：数字矩阵A∽B⇔①λE-A∽λE-B； ⇔②λE-A等价于λE-A；⇔③A,B相同的初等因子；⇔④A,B相同不变因子。
酉矩阵：AHA = AAH = E
正交矩阵：ATA = AAT = E
正规矩阵：AHA = AAH

一、线性空间与线性变换【矩阵来源、基础】

非空集合V内的元素α，β满足加法运算和数乘运算，k，s为数域F上任意数，
① 交换律 α+β = β+α；②结合律 α+(β+γ) = (α+β)+γ；③零元素 α+0 = α；④负元素 α+β = 0；
①1·α = α；②k(sα) = (ks)α；③(k+s)α = kα+sα；④k(α+β) = kα+kβ ；
则称非空集合V为数域F上的线性空间。文章来源地址https://www.toymoban.com/news/detail-815492.html

齐次线性方程组Ax = 0所有解的集合构成实数域R（复数域C）上的线性空间，就是这个线性方程组的解空间，叫做矩阵A的核空间或零空间，用N(A)表示。–>N(A)就是方程组的解空间
设A为实数（复数）m*n矩阵,x为n维列向量，则m维列向量y = Ax构成实数域R（复数域C）上的线性空间，称为A的列空间或者A的值域，用R(A) 表示。–>R(A)就是矩阵A列向量的线性组合
线性空间的基A与基B满足B=AP 过度矩阵P为可逆矩阵（就是线性变换），则By = Ax，则APy = Ax，则x = Py，y = P-1x。即不同基下坐标表换公式。
（A|E）–>（E|A-1）行变换、（A|B）–>（E|A-1B）行变换。
线性子空间：数域F上n维线性空间V的子集W满足：①α，β∈W，则α+β∈W；②α∈W，λ∈F，则λα∈W。
扩张空间：span{α1，α2，α3…} = k1α1+k2α2+k3α3+…–>基向量的线性组合
维数公式：dimV1+dimV2 = dim(V1+V2)+dim(V1∩V2)
求V1∩V2的基与维数：①列齐次线性方程组求公共解；②同一向量用两个基表示。
线性映射A :V1->V2满足：A(α1+α2) = A(α1)+A(α2)；A(λα) = λA(α)。A(α1,α2,…) =(β1,β2,…)·D，则矩阵D为线性映射A的矩阵表示。–>给定矩阵D可以确定唯一的线性映射A
线性映射：线性相关经过映射后一定线性相关。线性无关经过线性映射之后不一定线性无关。
V1->V2的线性映射在基{a}->{b}的矩阵表示为A，在基{a’}->{b’}的矩阵表示为B。{a}到{a’}的过度矩阵为P，{b}到{b’}的过度矩阵为Q，则AP=QB。
①B = QAP，B与A等价。②B = P-1AP，B与A相似。
n阶方阵A有n个特征根（值），对应的每个特征值λi可求相应的特征向量。这些特征向量加上零向量构成n维向量空间的一个子空间，称特征子空间。特征值对应的重根数为代数重复度，特征子空间的维数为几何重复度。—> 代数重复度：特征值的次数；几何重复度：对应特征向量的个数。

二、λ-矩阵与Jordan标准型【相似问题】

设aij(λ)为数域F上的多项式，则以aij(λ)为元素的m*n矩阵为多项式矩阵或λ矩阵。数字矩阵和特征矩阵λE - A都是λ矩阵的特例。
① r阶子式不为0，r+1阶子式全为0，则rank A(λ) = r。
② A(λ)B(λ) = B(λ)A(λ) = E，则B(λ)为A(λ)的逆矩阵，记作A-1(λ).
③ A(λ)可逆的充要条件：det A(λ) 为非零常数。—>与数字矩阵相同，行列式值不为零
设λ-矩阵A(λ)的左上角元素a11(λ)≠0，并且A(λ)中至少有一个元素不能被他整除，那么一定可以找到一个与A(λ)等价的矩阵B(λ)，它的左上角元素也不为零，但是次数比a11(λ)次数低。【Smith标准型化简原理，做初等变换】
Smith标准形：任意一个非零的m*n阶λ-矩阵A(λ)都等价于一个“对角形矩阵”，即A(λ) = diag{d1(λ), d2(λ), …, dr(λ), 0,0,0…}。其中r≥1，di(λ)是首项系数为1的多项式，且di(λ) | di+1(λ)。前一项能被后一项整除。
diag{d1(λ), d2(λ), …, dr(λ), 0,0,0…}即为A(λ)的Smith标准形。di(λ)为A(λ)的不变因子。
设λ-矩阵A(λ)的秩为r，对于正整数k，1 ≤ k ≤ r，A(λ)必有非零的k阶子式，A(λ)的全部k阶子式的首项系数为1的最大公因式Dk(λ)称为A(λ)的k阶行列式因子。等价矩阵有相同的个阶行列式因子，从而有相同的秩。Dk(λ) = d1(λ)d2(λ)…dk(λ)。dr(λ) = Dr(λ)/Dr-1(λ)。—>Smith标准型唯一
全部不变因子di(λ)分解为(λ-λi)乘积。则不为常数的因子全体叫做A(λ)的初等因子。指数某一项为0，则该列前面所有项次数均为0。—>不变因子相同，则初等因子相同。初等因子相同，若秩相同则不变因子相同。
Jordan标准型：因为只有部分矩阵可以相似对角化，故引入Jordan标准型，相似于准对角矩阵，类似对角矩阵。
设A∈Cn*n，A的初等因子为(λ-λ1)n1，(λ-λ2)n2，…(λ-λs)ns，则A∽J。J=diag{J1,J2,…Js}。所以A可对角化的充要条件为A的初等因子都是一次因式。
①求初等因子写Jordan标准型；②根据特征多项式写Jordan标准型，rank(λiE-A)=s1, rank(λiE-A)2=s2, rank(λiE-A)3=s3, rank(λiE-A)4=s4,…直到数值s不变。对应的λ = λi的Jordan块阶数如下：共有n-s1个块。阶数大于2的块有s1-s2个，大于3的有s2-s3个。大于r的有sr-1 - sr个。【两种方法】

三、内积空间与Hermite矩阵

设V是实数域R上的n维线性空间，对V中任意两个向量a,b依一确定法则对应着一个实数，这个实数称为内积，记作（a,b），并且要求内积（a,b）满足条件：①（a,b）=（b,a）②（ka,b）=k（a,b）③（a+b,c）=（a,c）+（b,c）④（a,a）≥0，当且仅当a=0时，（a,a）=0。有这样定义内积的n维线性空间称为n维欧氏空间。若在复数域C上，则为n维酉空间。【酉空间上的话计算注意取共轭】
内积空间性质：①（a,kb）=k’（a,b）;②（a,b+c）=（a,b）+（a,c）；③（∑kiai,b）=∑ki（ai,b）；④（a,∑kibi）=∑ki’（a,bi）。【①④要对k取共轭】
Hermite矩阵：AH=A则A为Hermite矩阵，AH=-A则A为反Hermite矩阵。AH为共轭转置矩阵。Hermite矩阵：对称位置实部相同，虚部相反。反Hermite矩阵：实部相反，虚部相同。
酉空间的度量：①非负性||a|| ≥ 0；②齐次性||ka|| = |k| ||a||；③三角不等式||a+b|| ≤ ||a|| + ||b||；④Cauchy-Schwarz不等式|(a,b)| ≤ ||a|| ||b||。
标准正交基，Schmidt正交化：①正交化b1 = a1；b2 = a2 - [(a2,b1)/(b1,b1)]b1；b3 = a3 - [(a3,b1)/(b1,b1)]b1 - [(a3,b2)/(b2,b2)]b2;…②单位化：v1 = b1/||b1||,…
酉矩阵：AHA = AAH = E，则称A为酉矩阵，记为A∈Unn。则①A-1 = AH∈Unn；②|detA| = 1；③AT∈Unxn；④AB，BA∈Unxn。正交矩阵：ATA = AAT =E。矩阵A是酉矩阵（正交矩阵）的充要条件是A的n个列（行）向量是标准正交向量组。
若a1,a2,…,ar为n为标准正交向量组，则nxr矩阵U1=(a1,a2,…ar)为次酉矩阵，记为U1∈Unxr。充要条件：U1HU1 = Er。
正规矩阵：若AHA = AAH,则A 为正规矩阵。ATA = AAT则A为实正规矩阵。
Hermite矩阵的性质：①A是Hermite矩阵，则Ak也是Hermite矩阵；②A是可逆的Hermite矩阵，则A-1也是Hermite矩阵；③A是Hermite矩阵（反Hermite矩阵）则iA是反Hermite矩阵（Hermite矩阵）；④A,B是Hermite矩阵，则kA + lB是Hermite矩阵；⑤A,B是Hermite矩阵，则AB是Hermite矩阵充要条件是AB= BA。A，B可交换。
设A∈Cnxn，则A是Hermite矩阵的充要条件是存在U∈Un*n，使得UHAU = diag(λ1,λ2,…λn)。特征值为实数。
n阶Hermite（实对称）矩阵A = （aij）正定的充要条件是A的n个顺序主子式全大于零。对于Hermite二次齐式f(X) = XHAX，X∈Cn则下列命题等价：
①f(X)是正定的；
②对于任意n阶可逆矩阵P，都有PHAP为正定矩阵；
③A的n个特征值全大于零；
④存在n阶可逆矩阵P使得PHAP = E；
⑤存在n阶可逆矩阵Q，使得A= QHQ；
⑥存在正线上三角矩阵R，使得A = RHR，且分解是唯一的。

四、矩阵分解

满秩分解
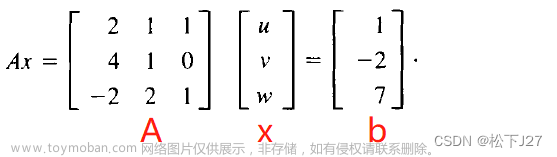
设A∈Cr mxn，则存在B∈Cr mxr, C∈Cr rxn，满足A=BC。 对A只做初等变换就可以得到A的满秩分解。经过初等行列变换可得：PAQ =[Er D; 0 0]。A = P-1[Er D;0 0]Q-1 = P-1[Er; 0] *[Er D]Q-1 = BC 。故B= P-1[Er;0], C = [Er D]Q-1。【初等行变换->B = A 中线性无关的r列，C=变换后的非零行，满秩分解不唯一】
正交三角分解
设A∈Cn nxn，则A可以唯一分解为A = UR或A= R1U1。 其中U,U1∈Un*n,R是正线上三角阵，R1是正线下三角阵。若A∈Cr mxr(列满秩矩阵)，则A可以唯一分解为A= UR，U∈Ur mxr，R是r阶正线上三角矩阵。若A∈Cr mxn，则A可以分解为A = U1R1L2U2。【直接对A作正交单位化–>U，R = UHA】
奇异值分解
设A∈Cr mxn，AAH的正特征值λi，AHA的正特征值ui，称ai =√λi=√ui是A的正奇异值，简称奇异值。
若A是正规矩阵，则A的奇异值是A的非零特征向量的模长。
若A∈Cr mxn，λ1 ≥ λ2 ≥ … ≥ λr是A的r个正奇异值，则存在m阶酉矩阵U和n阶酉矩阵V满足A = UDVH = U [Δ 0; 0 0]VH，其中Δ=diag(λ1,λ2,…λr),U满足UHAAHU是对角矩阵，V满足VHAHAV也是对角矩阵。【U=(u1,u2,…)为AAH非零特征值对应的特征向量，V=AHUΔ-H来计算】
谱分解
①正规矩阵的谱分解：设A为正规矩阵，那么存在U∈Unxn，满足A = Udiag(λ1,λ2,…λn)UH。若命U = (a1,a2,…an)，则A = （a1,a2,…an）diag(λ1,λ2,…λn)（a1H,a2H,…anH）T = λ1a1a1H + λ2a2a2H+…。其中ai是矩阵A的特征值为λi的所对应的单位特征向量，a1a1H是n阶矩阵，即为谱分解。
设n阶矩阵A有r个相异特征值λ1，λ2，…λr，λi的代数重复度为ni，则A为正规矩阵的充要条件是存在r个n阶矩阵G1,G2,…Gr,满足：(1)A = ∑λiGi; (2)Gj = Gj2 = GjH [幂等矩阵，Hermite矩阵]; (3)GjGk = 0; (4)∑Gj = E; (5)满足上述性质的Gj唯一; (6)rank Gj = nj。
②单纯矩阵的谱分解：设A为单纯矩阵（即A可对角化），特征值为λ1,…,λn，其对应的特征向量分别为a1,…an，若命P = （a1,a2,…an）,则A = Pdiag(a1,a2,…an)P-1 = λ1a1b1T+λ2a2b2T+…
分解步骤：(1)先求出矩阵A的特征值λi与特征向量ai；(2)根据矩阵转置的性质得到(P-1)T = (b1,b2,…bn)；(3)令Gi = aibiT+…(同一特征值对应的多个特征向量的求和)，A = λ1G1 + λ2G2 + …

五、矩阵范数、序列、级数

向量范数
设V是数域F(实数域R或复数域C)上的线性空间，用||x||表示按照某个法则确定的与向量x对应的实数，且满足:（1）非负性：||x|| ≥ 0，当且仅当x=0时||x|| = 0；（2）齐次性||kx|| = |k| ||x||；（3）三角不等式||x+y|| ≤ ||x|| + ||y||，则称||x||是向量x的范数。
Holder不等式(赫尔德)：∑akbk ≤ (∑akp)1/p (∑bkq)1/q。【k为求和下标，q,p为幂次】
Minkowski不等式(闵可夫斯基)：( ∑|ai+bi|p )1/p ≤ （∑|ai|p）1/p + （∑|bi|p）1/p。【i为下标，p为幂次】
设向量x = (x1,x2,…xn)T对任意p≥1，称量||x||p = (∑ |xi|^p) 1/p为向量x的p-范数。常用范数有三种：
①1-范数：||x||1 = ∑|xi|；【元素和】
②2-范数：||x||2 = (∑ |xi|2) 1/2 = (xHx)1/2；【欧式范数】
③∞-范数：||x||∞ = lim||x||p = max|xi|。【最大元素值】
范数等价性定理：设V是n维线性空间，||x||a和||x||b为任意两种向量范数（不限于p-范数），则总存在正数c1,c2，对V中所有向量x∈V恒有：c1||x||b ≤ ||x||a ≤ c2||x||b。
矩阵范数
矩阵范数满足非负性、齐次性、三角不等式和矩阵乘法相容性：若A与B可乘，有||AB|| ≤ ||A|| ||B||。则对应的实数||A||为矩阵A的矩阵范数。
Frobenius范数：若A = （aij）∈Cmxn，规定||A||F = （∑∑|aij|^2）1/2。【各元素平方和开二次根】是向量范数中欧式范数的形式推广。性质：（1）若A = （a1,a2,…an），则||A||F 2 = ∑||ai||2 2；（2）||A||F 2 = tr(AHA) = ∑λi(AHA)；（3）对于任何m阶酉矩阵U与n阶酉矩阵V，都有等式||A||F = ||UA||F = ||AH||F = ||AV||F = ||UAV||F。
诱导范数（算子范数）
相容的矩阵范数：设||x||a是向量范数，||A||b是矩阵范数，若对于任意矩阵A和向量x都满足 ||Ax||a ≤ ||A||b ||x||a，则称||A||b为与向量范数||x||a相容的矩阵范数。
||A||p = max ||Ax||p / ||x||p即为向量p-范数所诱导的矩阵范数为矩阵p-范数。常用矩阵范数为：
①||A||1 = max j(∑|aij|)；【最大列和】
②||A||2 = max j(λj(AHA))1/2，λj(AHA)表示矩阵AHA的第j个特征值。||A||2称为谱范数，是A的最大正奇异值。
③||A||∞ = max i(∑|aij|)。【最大行和】
谱半径：设A∈Cnxn，A的n个特征值为λ1，λ2，…λn,则称ρ(A) = max{|λi|}是A的谱半径。ρ(A) ≤ ||A||，其中||A||是A的任一种范数。
矩阵序列极限
①对于矩阵A的某一种范数||A|| ＜ 1，则lim Ak = 0;【k次幂】
②ρ(A) < 1 等价于lim Ak = 0；【k次幂】
③{Ak}收敛于A等价于lim ||Ak - A|| = 0。【k为下标】
矩阵幂级数
①矩阵级数：每一个元素都绝对收敛的时候，则矩阵级数绝对收敛。矩阵级数∑Ak绝对收敛的充要条件为：正项数项级数∑||Ak||，其中||A||为任何一种矩阵范数。
②若矩阵幂A的某一种范数||A||在幂级数c0+c1x+c2x2+…的收敛域内，则矩阵幂级数c0E +c1A+c2A2+…绝对收敛。

六、矩阵函数

用矩阵函数的Jordan表示计算矩阵函数的步骤：
①求A的Jordan标准型，J = diag(J1,J2,…,Jr)
②由J写出f(J) = diag(f(J1),f(J2),…f(Jr))
③由J计算变换矩阵P，满足AP = PJ。
④写出f(A)的Jordan表示式f(A) = Pf(J)P-1
⑤把所求矩阵函数f(A)所对应的函数f(x)带入Pf(J)P-1。
化零多项式：
给定矩阵A∈Cnxn，如果多项式p(λ) = amλm + …+a1λ+a0,满足p(A) = 0，则称p(λ)为A的化零多项式。
最小多项式：
在A的化零多项式中，次数最低且首项稀疏为1的化零多项式称为A的最小多项式。记为ψA(λ).
①方阵A的任意化零多项式都能被ψA(λ)整除；
②A的最小多项式ψA(λ)是唯一的；
③相似矩阵的最小多项式相同。
矩阵函数的多项式表示：
p(x) = a0+a1x+a2x2+…+am-1xm-1。
①写出最小多项式；
②根据次数取p(x)的前k项；
③解出a0,a1,…ak-1;
④带入f(A) = p(A) = a0E + a1A+… + ak-1Ak-1