树的性质与遍历
树者,千载之长存也。
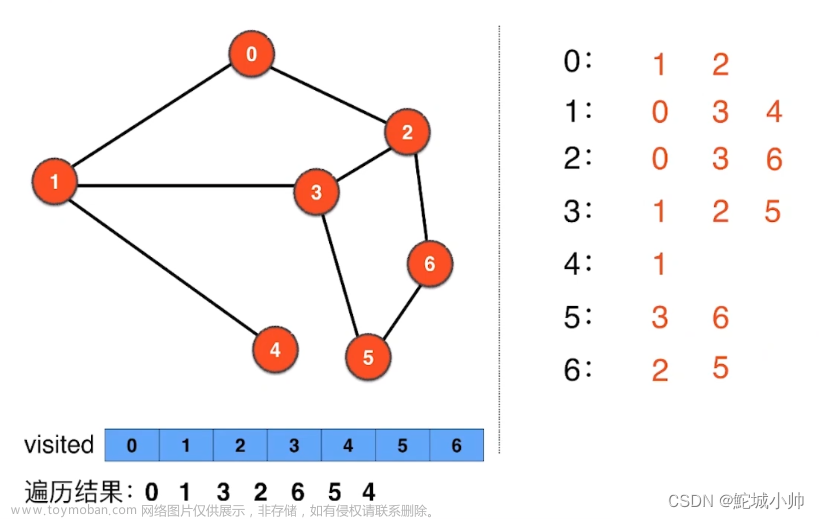
树的性质与遍历树的性质:树的遍历:
树的性质:
-
无向连通性
树是一个无向连通图,也就是说,任意两个节点之间存在唯一的路径。
-
无回路
树不包含任何回路或环,也就是说,不存在任何节点能够经过若干条边回到自身。
-
N-1条边
一个树由 N 个节点组成,其中有 N-1 条边连接这些节点。
-
唯一路径
在树中,任意两个节点之间存在唯一的路径,也就是说,从树的根节点出发,可以通过唯一的路径到达任意一个节点。
-
无向无权图
树是一种无向无权图,即每条边没有权重或距离的概念。
-
最小连通子图
对于给定的连通图,如果删除任意一条边,都会使得图不再连通,那么这个连通图就是一棵树。换句话说,树是最小连通子图。
树的遍历:
-
深度优先遍历
搜索路径、连通性等问题
板子:
using namespace std;
const int N = 1e5 + 7;
vector<int> v[N];
bool use[N];
int n, d,ans = 0;
void dfs(int pos, int val) {
if (val == d) return;
use[pos] = 1;
for (int i = 0; i < v[pos].size(); i++)
if (use[v[pos][i]] == 0) {
use[v[pos][i]] = 1;
dfs(v[pos][i], val + 1);
ans++;
}
}
int main() {
cin >> n>>d;
int begin, to;
for (int i = 1; i <= n-1; i++) {
cin >> begin >> to;
v[begin].push_back(to);
v[to].push_back(begin);
}
dfs(1, 0);
cout << ans;
}
-
广度优先遍历
寻找最短路径、层级分析等问题
板子(注意,只是普通广搜,若要涉及最短路,则在后面章节)
using namespace std;
const int N = 1e5 + 7;
vector<int> v[N];
bool use[N];
int n, d;
int main() {
cin >> n>>d;
int begin, to;
for (int i = 1; i <= n-1; i++) {
cin >> begin >> to;
v[begin].push_back(to);
v[to].push_back(begin);
}
queue<int> q;
q.push(1);
use[1] = 1;
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < v[now].size(); i++) {
if (use[v[now][i]] == 0) {
q.push(v[now][i]);
}
use[v[now][i]] = 1;
}
}
}
注意事项:
-
注意题给信息决定是否要建立反向边
-
对于无向图,要注意开标记数组
树的直径与重心
“万木悉自寒,孤松独秀时。重心在地底,直径正天涯。”——白居易
树的直径与重心树的直径:定义求法注意树的重心定义性质求法换根DP求重心代码:
树的直径:
定义
树的直径是指树中最长路径的长度。也可以理解为在树中任选两个节点,它们之间的最长路径的长度即为树的直径。
求法
首先从任意节点开始进行一次深度优先搜索,找到距离该节点最远的节点A。然后从节点A开始进行第二次深度优先搜索,找到最远的节点B,那么节点A和节点B之间的路径长度就是树的直径。
注意
一棵给定的树中,直径的长度是一定的,但直径的路径是不一定的
树的重心
定义
将树中的某一结点删除,这棵树将散架,分成若干棵子树,设其中最大的一棵树结点数量为 N。以此类推,遍历每一个结点,找到最小的N,此时删除的结点就是重心
性质
-
树的重心如果不唯一,则至多有两个,且这两个重心相邻。
-
以树的重心为根时,所有子树的大小都不超过整棵树大小的一半。
-
树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。
-
把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。
-
在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
求法
比较常见的求法是换根dp。
这种求法不是通过重心的定义来求解,而是通过重心的一个性质,
也就是树中所有的点到重心的距离之和最小
怎么实现的?
我们假设
n为所有结点的个数
Sum_distance[i]表示树上所有的点到i的的距离之和。
Size[i]表示以i根的子树的大小。
对树上的任意一个非根结点x,设其父结点为y,有转移方程Sum_distance[x]=Sum_distance[y] + (n-Size[x]) - Size[x]
解释一下:
我们的状态转移是从根节点开始,慢慢向下转移。
所以对于x的父结点y ,其状态已经被计算过了。
我们现在要往下移动一个单位到其儿子x,那么对于x的子树部分的任意一个结点,其到 x的距离就等于其到 y的距离-1,总共减少的距离是Size[x]
对于非x的子树部分的任意一个结点,其到x的距离就等于其到y的距离+1,总共增加的距离是n-Size[x]
那么,很显然,需要改变的距离是能计算出来的。
也就是(n-Size[x]) - Size[x]
化简后的式子就是:Sum_distance[x]=Sum_distance[y] + n - 2*Size[x]
换根DP求重心代码:
1、先求出每个结点子树大小
void get_size(int now,int fa) { // fa指的是当前这个点的父结点
Size[now] = 1;//now结点的子树大小初始化为1
for (int i = 0; i < v[now].size(); i++) {
if (v[now][i] != fa) { //不能回头搜索
get_size(v[now][i], now);
Size[now] += Size[v[now][i]];
}
}
}
2、求出树中所有的点到根节点的距离之和
ps:即求每个点的深度之和
int get_d1(int now,int fa,int depth) {
int ans = 0;
for (int i = 0; i < v[now].size(); i++)
if (v[now][i] != fa)
ans+=get_d1(v[now][i],now,depth+1)+depth;
return ans;
}
3、换根DP过程文章来源:https://www.toymoban.com/news/detail-815757.html
ps:use[i]是标记数组,用来记录这个点是否被搜过文章来源地址https://www.toymoban.com/news/detail-815757.html
void get_alld(int now, int fa) {
use[now] = 1;
for (int i = 0; i < v[now].size(); i++) {
if (son != fa and use[son] == 0) {
d[v[now][i]] = d[now] + Size[1] - 2 * Size[v[now][i]];
get_alld(v[now][i], fa);
}
}
} 到了这里,关于图论中的树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!