Java数据结构——二叉树的遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了Java数据结构——二叉树的遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

java 二叉树遍历,JavaSE零基础学习,Java数据结构,数据结构,链表,算法

作者：敲代码の流川枫

博客主页：流川枫的博客

专栏：和我一起学java

语录：Stay hungry stay foolish

工欲善其事必先利其器，给大家介绍一款超牛的斩获大厂offer利器——牛客网

点击注册和我一起刷题

文章目录

1.创建二叉树

2.二叉树的三种遍历方式

3.代码实现遍历

前序遍历

中序遍历

后序遍历

1.创建二叉树

二叉树的存储结构分为：顺序存储和类似于链表的链式存储，这里我们学习链式存储的方式，简单枚举一棵二叉树，二叉树的真正创建方式，后续会介绍

我们使用孩子表示法创建：

// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}

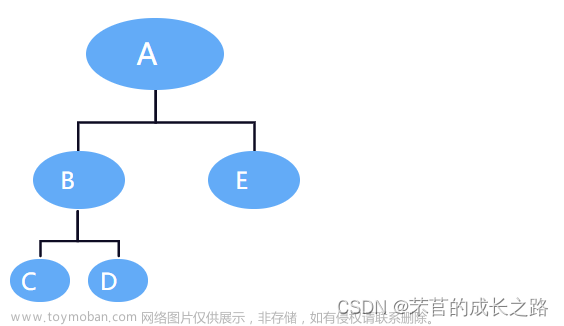
一共有八个节点

java 二叉树遍历,JavaSE零基础学习,Java数据结构,数据结构,链表,算法

public class TestBianryTree {
    static class TreeNode{
        public char val;
        public TreeNode left;
        public TreeNode right;
        public TreeNode(char val){
            this.val = val;
        }
    }
    public TreeNode creatTree(){
        TreeNode A = new TreeNode('A');
        TreeNode B = new TreeNode('B');
        TreeNode C = new TreeNode('C');
        TreeNode D = new TreeNode('D');
        TreeNode E = new TreeNode('E');
        TreeNode F = new TreeNode('F');
        TreeNode G = new TreeNode('G');
        TreeNode H = new TreeNode('H');

        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        C.left = F;
        C.right = G;
        E.right = H;

        return A;
    }
}

2.二叉树的三种遍历方式

java 二叉树遍历,JavaSE零基础学习,Java数据结构,数据结构,链表,算法

先序遍历：根——>左——>右

遍历结果： ABDEHCFG

中序遍历：左——>根——>右

遍历结果：DBEHAFCG

后序遍历：左——>右——>根

遍历结果：DHEBFGCA

例题：

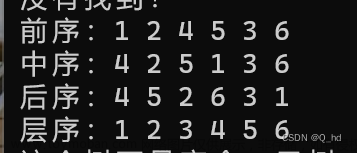
设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为()

A: adbce B: decab C: debac D：abcde

由后序遍历访问规律为左右根可得，a为根节点，中序遍历访问规律为左根右得，b为a左数，dce为a右树部分，后序遍历得c为一个根节点，则de分别为c的左右子树，前序遍历规律为根左右，选D

图为：

某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出(同一层从左到右)的序列为() A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF

先可以确定根为F，然后根据中序的左右子树分布特点，这棵二叉树没有右子树

选A

思考：给定一个前序遍历和后序遍历能不能创建出来一颗二叉树？

是不能的，因为前序遍历和后续遍历只能确定根节点，确定不了左子树和右子树的位置

3.代码实现遍历

前序遍历

代码

 // 前序遍历
    public void preOrder(TreeNode root){
        if(root == null){
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

结果

java 二叉树遍历,JavaSE零基础学习,Java数据结构,数据结构,链表,算法

中序遍历

代码

// 中序遍历
    void inOrder(TreeNode root){
        if(root == null){
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

结果

java 二叉树遍历,JavaSE零基础学习,Java数据结构,数据结构,链表,算法

后序遍历

 // 后序遍历
    void postOrde(TreeNode root){
        if(root == null){
            return ;
        }
        postOrde(root.left);
        postOrde(root.right);
        System.out.print(root.val+" ");

    }

结果

java 二叉树遍历,JavaSE零基础学习,Java数据结构,数据结构,链表,算法