【蓝桥杯--图论】Dijkstra、Ballman-Ford、Spfa、Floyd-Toy模板网

这篇具有很好参考价值的文章主要介绍了【蓝桥杯--图论】Dijkstra、Ballman-Ford、Spfa、Floyd。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【蓝桥杯--图论】Dijkstra、Ballman-Ford、Spfa、Floyd,数据结构与算法,蓝桥杯,图论

今日语录：每一次挑战都是一次成长的机会

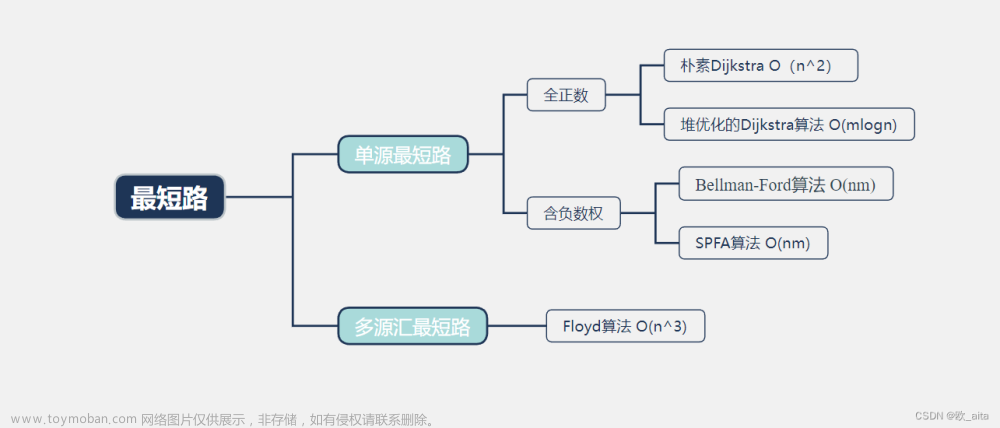
如上所示即为做题时应对的方法

朴素DIjkstra

引用与稠密图，即m<n^2

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    // 将距离初始化为无穷大
    dist[1] = 0;

    for (int i = 0; i < n; i++)
    {
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = true;

        for (int j = 1; j <= n; j++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf(" % d % d", &n, &m);

    memset(g, 0x3f, sizeof g);

    while (m--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);
    }

    int t = dijkstra();
    
    printf("%d\n", t);
    return 0;
}

堆优化的Dijkstra

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

typedef pair<int, int>PII;

const int N = 10010;

int n, m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a],h[a]=idx++;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    //初始化距离为无穷
    dist[1] = 0;

    priority_queue<PII, vector<PII>, greater<PII>>heap;
    heap.push({ 0,1 });

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;
        if (st[ver])continue;

        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > distance + w[i])
            {
                dist[j] = distance + w[i];
                heap.push({ dist[j],j });
            }
        }

    }
    
    if (dist[n] == 0x3f3f3f3f)return -1;
    return dist[n];

}

int main()
{
    scanf(" % d % d", &n, &m);

    memset(h, -1, sizeof h);

    while (m--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    int t = dijkstra();
    
    printf("%d\n", t);
    return 0;
}

Ballman-Ford

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 510,M = 10010;

int m, n,k;
int dist[N], backup[N];

struct Edge
{
    int a, b, w;
}edges[M];

int bellman_ford()
{

    memset(dist, 0x3f, sizeof dist);
    for (int i = 0; i < k; i++)
    {
        memcpy(backup, dist, sizeof dist);
        for (int j = 0; j < m; j++)
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
    if (dist[n] > 0x3f3f3f3f / 2)return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d%d", &n, &m, &k);

    for (int i = 0; i < m; i++)
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = { a,b,w };
    }

    int t = bellman_ford();

    if (t == -1)puts("impossible");
    else printf("%d\n", t);

    return 0;
}

Floyd

#include<iostream>
#include<cstring>
#include<algorithm>
#define _CRT_SECURE_NO_WARNINGS

using namespace std;
const int N = 210,INF = 1e9;

int n, m,Q;
int d[N][N];

void floyd()
{
	for (int k = 1; k <= n; k++)
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= n; j++)
				d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main()
{
	scanf("%d%d%d", &n, &m, &Q);

	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			if (i == j)d[i][j] = 0;
			else d[i][j] = INF;

	while (m--)
	{
		int a, b, w;
		scanf("%d%d%d", &a, &b, &w);

		d[a][b] = min(d[a][b], w);
	}

	floyd();
	while (Q--)
	{
		int a, b;
		scanf("%d%d", &a, &b);

		if (d[a][b] > INF / 2)puts("impossible");
		else printf("%d\n", d[a][b]);
	}
	return 0;
}

Spfa(求最短路)

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

typedef pair<int, int>PII;

const int N = 10010;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int>q;
    q.push(1);
    st[1] = true;

    while (q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    if (dist[n] == 0x3f3f3f3f)return -1;
    return dist[n];
}

int main()
{
    scanf(" % d % d", &n, &m);

    memset(h, -1, sizeof h);

    while (m--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    int t = spfa();

    printf("%d\n", t);
    return 0;
}

Spfa（求是否含有负权）

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#define _CRT_SECURE_NO_WARNINGS

using namespace std;
typedef pair<int, int>PII;
const int N = 10010;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N],cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int spfa()
{
    queue<int>q;
    for (int i = 1; i <= n; i++)
    {
        st[i] = true;
        q.push(i);
    }

    while (q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];

                cnt[j] = cnt[t] + 1;

                if (cnt[j] >= n)return true;
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return false;
}

int main()
{
    scanf(" % d % d", &n, &m);

    memset(h, -1, sizeof h);

    while (m--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    if (spfa())puts("Yes");
    else puts("No");
    return 0;
}