02【评价类】模型——TOPSIS法(理想解法、优劣解距离法)
目录
02【评价类】模型——TOPSIS法(理想解法、优劣解距离法)
一、引述
二、TOPSIS法的应用
2.1 决策矩阵正向化处理
2.1.1 效益型指标(极大型指标)
2.1.2 成本型指标(极小型指标)
2.1.3 区间型指标
2.1.4 中间型指标
2.1.5 问题解决
2.2 正向化矩阵规范化处理
2.3 构造指标的权重向量
2.3.1 层次分析法求权重向量
2.3.2 熵权法求权重向量
2.3.3 默认权重向量
2.3.4 问题解决
2.4 求各方案到正、负理想解的距离
2.4.1 求正、负理想解
2.4.2 求各方案与正、负理想解的距离
2.4.3 求综合指标值
三、TOPSIS法程序实现
四、总结
一、引述
TOPSIS法(Technique for Order Preference by Similarity to Ideal Solution) 可翻译为逼近理想解排序法,国内常简称为优劣解距离法 TOPSIS 法是一种常用的综合评价方法,其能充分利用原始数据的信息, 其结果能精确地反映各评价方案之间的差距。
引例:研究生院试评估。
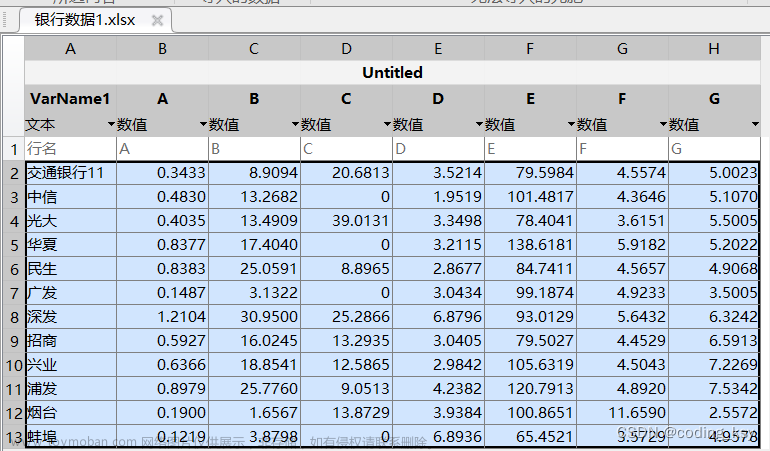
为了客观地评价我国研究生教育的实际状况和各研究生院的教学质量,国务院学位委员会办公室组织过一次研究生院的评估。为了取得经验,先选5所研究生院,收集有关数据资料进行了试评估,图1-1是所给出的部分数据。

由此表格可得到决策矩阵为:
注:第行第列为。
二、TOPSIS法的应用
2.1 决策矩阵正向化处理
2.1.1 效益型指标(极大型指标)
一个指标越大越好,则称为效益型指标或极大型指标;
比如:一个学生的成绩,国家的GDP,一个公司的利润等;本例中的“人均专著”即为效益型指标。
注:该指标为统一型指标,即下面三种指标需要正向化处理为该类型指标。
2.1.2 成本型指标(极小型指标)
一个指标越小越好,则称为成本型指标或极小型指标;
比如:一个工厂某种产品的成本,一个人的负面评价等;本例中的“科研经费”和“逾期毕业”即为成本型指标。
成本型指标转化成效益型指标的值为:
或
2.1.3 区间型指标
一个指标的值落在某个区间最好,则称为区间型指标;
比如:人体温度(36~37℃);本例中的“生师比”即为区间型指标。
区间型指标转化成效益型指标的值为:
其中是一组区间型指标序列,且最佳区间为.
公式解释如下,

根据公式以及图2-1可知,其中的值为,即为图2-1中红色段的长度。对于公式的右半部分,以的情况为例(即落在红色段),即表示距离最佳区间的距离,以该值作为分子,以距离最佳区间的距离作为分母。则表示与最佳区间的远近程度(离最佳区间越远该值越大,越近该值越小),显然这是一个成本型指标,所以为了转化成效益型指标,我们用1减去(即,显然是属于的),那么就将区间型指标转化成了效益型指标。下面的和的情况同理可得。
2.1.4 中间型指标
一个指标越靠近某个中间值越好,则称为中间型指标;
比如:河水的PH值(PH=7)。
中间型指标转化为效益型指标的值为:
公式解释如下,

根据公式以及图2-2可知,其中的值为,即图2-2红色段的长度。公式的右半部分即表示与的距离并作为分子,与的最大距离作为分母;用来描述与的远近程度(与距离越远该值越大,越近该值越小),显然这是一个成本型指标,因此我们用1减去(即,显然是属于的)来将其转化为效益型指标。
2.1.5 问题解决
将决策矩阵正向化处理之后得到正向化矩阵:
其中可由(2.1.2,2.1.3和2.1.4)中的公式求得。
2.2 正向化矩阵规范化处理
为了去除量纲的影响,因此我们需要对已得到的正向化矩阵进行规范化处理,得到规范化矩阵:
其中.
上面公式可解释为,规范化矩阵的每一个元素即为正向化矩阵的对应元素/
。
2.3 构造指标的权重向量
2.3.1 层次分析法求权重向量
求权重向量即为各指标求其所占权重,我们首先根据成对比较阵标度表对指标两两进行比较,从而得到判断矩阵(成对比较矩阵),然后依照层次分析法的步骤流程来得到权重向量,
其中,的具体求法请参照本系列其他文章(01层次分析法)。
2.3.2 熵权法求权重向量
具体求法请参照本系列的其他文章(03熵权法)。
2.3.3 默认权重向量
若不采取上面两种方法构造权重向量,则采取默认权重向量,
其中,n为决策矩阵的列数,即指标的个数。
2.3.4 问题解决
在本引例中,采取默认权重向量,即
.
在求得规范化矩阵和指标的权重向量后可得到加权规范阵:
其中,。
2.4 求各方案到正、负理想解的距离
2.4.1 求正、负理想解
正理想解为:
其中,。
正理想解即位每个指标在各方案之间的最大值。
负理想解为:
其中, 。
负理想解即位每个指标在各方案之间的最小值。
2.4.2 求各方案与正、负理想解的距离
其中,.
其中, 。
这里的与正、负理想解的距离采用的是欧几里得距离(欧氏距离)。
2.4.3 求综合指标值
在求得各方案与正负理想解的距离后,则可以得到各个方案的综合指标值(即各方案得分):
其中 .
再将综合指标归一化,
其中,.
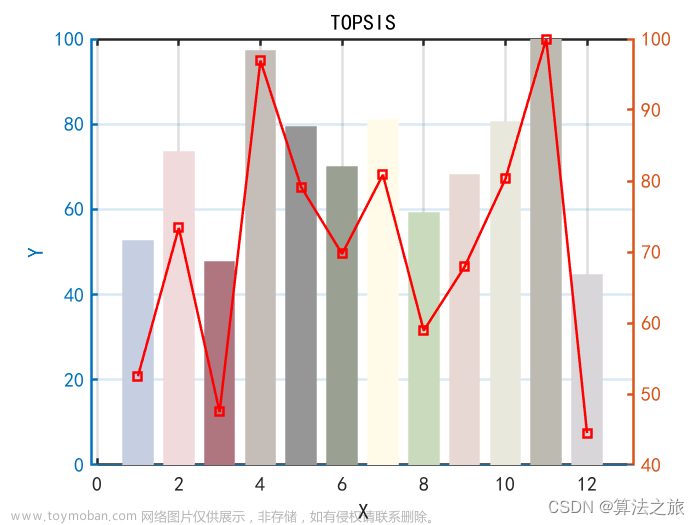
由数据可知,第5所研究院的综合指标值(0.3035)最高。
归一化:归一化的目的就是使得预处理的数据被限定在一定的范围内(比如[0,1]或[-1,1]),从而消除奇异样本数据导致的不良影响。奇异样本数据是指相对于其他输入样本特别大或特别小的样本值。(标准化,规范化又是什么呢?)
三、TOPSIS法程序实现
TOPSIS法的代码实现如下:
//FileName:G_TOPSIS.m(主程序)
%% TOPSIS
% 程序的预处理部分
clear;clc;
disp('请输入决策矩阵');
A=input('A=');
disp('请输入各列的指标类型(1.效益型,2.成本型,3.区间型,4.中间型):');
Type=input('Type=');
[n1,n2]=size(A);
%% 决策矩阵正向化处理
% 将成本型、区间型和中间型指标转化为效益型指标
X=zeros(n1,n2);
for i=1:n2
switch Type(i)
case 1
X(:,i)=A(:,i);
case 2
X(:,i)=G_Min2Max(A(:,i));
case 3
disp('请输入区间的上下界a,b:');
a=input('a=');
b=input('b=');
X(:,i)=Inter2Max(A(:,i),a,b);
case 4
disp('请输入最好值value:');
value=input('value=');
X(:,i)=Mid2Max(A(:,i),value);
otherwise
disp('您输入的Type中的数据包含不属于1~4的数据,请修改!');
end
end
%% 正向矩阵规范法处理
% 为了将已正向化的矩阵消除量纲的影响,则需要对其进行规范化处理
sum_X=sqrt(sum(X.*X));
B=X./repmat(sum_X,n1,1);
%% 求加权规范矩阵
% 一个方案的各指标的重要程度不同,则需要对各指标赋予权值
% 构造权重向量主要方法有:层次分析法,熵权法和默认方法
weigh=ones(1,n2)./n2;%默认方法
C=B.* repmat(weigh,n1,1);
%% 计算与正负理想解的距离
C_up=max(C);% C_up(j)表示第j个指标的正理想解
C_down=min(C);
temp1=C-repmat(C_up,n1,1);%temp1为cij-C_up(j)的差值
temp2=C-repmat(C_down,n1,1);
D_up=sum(temp1.^2,2).^0.5;%D_up(i)即为第i个方案与正理想解的距离
D_down=sum(temp2.^2,2).^0.5;
result=D_down./(D_up+D_down);%计算各方案的综合指标
disp('result=');
disp(result);
[sort_result,index]=sort(result,'descend');
disp('sort_result=');
disp(sort_result);
disp('index');
disp(index);下面三个代码段为正向化处理时所用到的函数:
//FileName:G_Min2Max.m(成本型效益型)
function [f1]=G_Min2Max(X)
% X表示需要正向化的决策矩阵的某一列
[n1,~]=size(X);
f1=repmat(max(X),n1,1)-X;
end//FileName:G_Min2Max.m(区间型效益型)
function [f2]=G_Inter2Max(X,a,b)
% X表示需要正向化的决策矩阵的某一列
% a,b分别表示最佳区间的上下限
M=max([a-min(X),max(X)-b]);%向量X中的所有元素与最佳区间[a,b]的最远距离
f2=ones(size(X),1);
for i=1:size(X)
if i<a
f2(i)=1-(a-X(i))/M;%当X(i)小于a时的公式
elseif i>b
f2(i)=1-(X(i)-b)/M;
else
f2(i)=1;
end
end
end//FileName:G_Min2Max.m(中间型效益型)
function [f3]=G_Mid2Max(X,value)
% X表示需要正向化的决策矩阵的某一列
% value表示处于中间的最好值
M=max(abs(X-value));
f3=1-abs(X-value)/M;
end四、总结
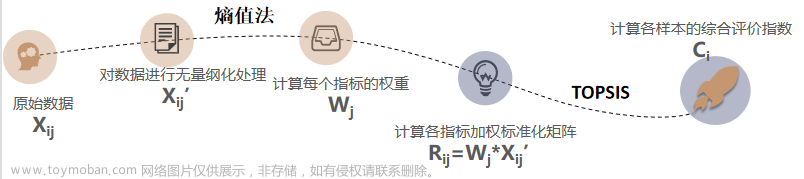
用TOPSIS法解决评价类问题时整体实现的流程:

小结:
- TOPSIS法是对于各指标的数据都是已知的,而层析分析法的几乎没有任何数据;
- 因为熵权法存在缺陷,所以平时发表论文时一般不使用,而数模比赛时可以用。
疑问:
- 归一化、标准化和规范法有什么异同?
- 在写论文时,需要对指标正向化的公式进行解释吗?
结束语:本文部分内容来自于B站“数学建模学习交流”以及疯学网数学建模系列教程文章来源:https://www.toymoban.com/news/detail-817599.html
文章来源地址https://www.toymoban.com/news/detail-817599.html
到了这里,关于02【评价类】模型——TOPSIS法(理想解法、优劣解距离法)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!