图论可达性c语言实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论可达性c语言实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

概述

图论中的可达性是指在图中是否存在从一个顶点到另一个顶点的路径。这是图论中的一个基本概念，对于许多实际问题的建模和解决都非常重要。以下是关于图论可达性的一些重要概念和信息：

有向图和无向图： 图可以分为有向图和无向图。在有向图中，边有方向，从一个顶点到另一个顶点的路径是有向的。在无向图中，边没有方向，路径是无向的。
可达性定义： 在有向图中，从顶点A到顶点B的可达性表示存在一条有向路径从A到B。在无向图中，如果存在一条路径从顶点A到顶点B，那么A和B被认为是可达的。
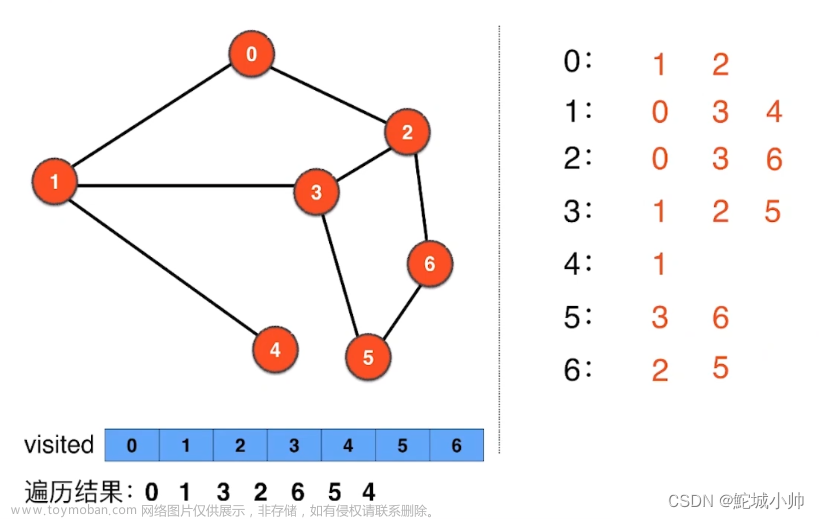
深度优先搜索（DFS）： DFS是一种用于遍历图的算法，可以用来检查可达性。通过从起始顶点开始，尽可能深入图中，直到无法继续为止。DFS可以用来查找路径并判断两个顶点之间是否可达。
广度优先搜索（BFS）： BFS是另一种遍历图的算法，它从起始顶点开始，逐层遍历图。BFS也可以用于检查可达性，并找到最短路径。
图的表示： 图可以通过邻接矩阵或邻接表等方式表示。邻接矩阵是一个二维数组，其中元素表示顶点之间的连接关系。邻接表是一种更灵活的表示方法，使用链表来表示每个顶点的邻接顶点。
应用： 可达性在许多领域都有重要应用，如网络路由、社交网络分析、数据库查询优化等。在计算机科学和工程中，图的可达性是解决许多实际问题的关键步骤。

总的来说，图论中的可达性是一个关键的概念，它帮助我们理解图结构中的路径和连接关系，为解决各种问题提供了强大的工具。

以下是无向图的可达性实现代码。

无向图完整代码

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 100

// 定义图的结构
struct Graph {
    int vertices;          // 图的顶点数
    int adjacencyMatrix[MAX_VERTICES][MAX_VERTICES];  // 邻接矩阵表示图的连接关系
};

// 函数声明
void initGraph(struct Graph* graph, int vertices);
void addEdge(struct Graph* graph, int start, int end);
void DFS(struct Graph* graph, int vertex, int visited[MAX_VERTICES]);
void checkReachability(struct Graph* graph, int start, int end);

int main() {
    struct Graph graph;
    int vertices, edges, start, end;

    // 输入图的顶点数和边数
    printf("输入图的顶点数和边数：");
    scanf("%d %d", &vertices, &edges);

    initGraph(&graph, vertices);

    // 输入图的边
    printf("输入图的边（每行包含两个顶点，表示一条边）：\n");
    for (int i = 0; i < edges; i++) {
        int startVertex, endVertex;
        scanf("%d %d", &startVertex, &endVertex);
        addEdge(&graph, startVertex, endVertex);
    }

    // 输入要检查可达性的起始点和结束点
    printf("输入要检查可达性的起始点和结束点：");
    scanf("%d %d", &start, &end);

    // 检查可达性
    checkReachability(&graph, start, end);

    return 0;
}

// 初始化图
void initGraph(struct Graph* graph, int vertices) {
    graph->vertices = vertices;

    // 初始化邻接矩阵
    for (int i = 0; i < vertices; i++) {
        for (int j = 0; j < vertices; j++) {
            graph->adjacencyMatrix[i][j] = 0;
        }
    }
}

// 添加边
void addEdge(struct Graph* graph, int start, int end) {
    // 有向图，将起始点到结束点的边标记为1
    graph->adjacencyMatrix[start][end] = 1;
}

// 深度优先搜索
void DFS(struct Graph* graph, int vertex, int visited[MAX_VERTICES]) {
    visited[vertex] = 1;
    printf("%d ", vertex);

    for (int i = 0; i < graph->vertices; i++) {
        if (graph->adjacencyMatrix[vertex][i] == 1 && !visited[i]) {
            DFS(graph, i, visited);
        }
    }
}

// 检查可达性
void checkReachability(struct Graph* graph, int start, int end) {
    int visited[MAX_VERTICES] = {0};

    printf("从顶点 %d 出发，DFS 遍历结果为：", start);
    DFS(graph, start, visited);

    if (visited[end]) {
        printf("\n%d 可达 %d\n", start, end);
    } else {
        printf("\n%d 不可达 %d\n", start, end);
    }
}

测试无向图

图论可达性c语言实现,图论,c语言,深度优先

有向图完整代码

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 100

// 定义图的结构
struct Graph {
    int vertices;          // 图的顶点数
    int adjacencyMatrix[MAX_VERTICES][MAX_VERTICES];  // 邻接矩阵表示图的连接关系
};

// 函数声明
void initGraph(struct Graph* graph, int vertices);
void addEdge(struct Graph* graph, int start, int end);
void DFS(struct Graph* graph, int vertex, int visited[MAX_VERTICES]);
void checkReachability(struct Graph* graph, int start, int end);

int main() {
    struct Graph graph;
    int vertices, edges, start, end;

    // 输入图的顶点数和边数
    printf("输入图的顶点数和边数：");
    scanf("%d %d", &vertices, &edges);

    initGraph(&graph, vertices);

    // 输入图的边
    printf("输入图的边（每行包含两个顶点，表示一条边）：\n");
    for (int i = 0; i < edges; i++) {
        int startVertex, endVertex;
        scanf("%d %d", &startVertex, &endVertex);
        addEdge(&graph, startVertex, endVertex);
    }

    // 输入要检查可达性的起始点和结束点
    printf("输入要检查可达性的起始点和结束点：");
    scanf("%d %d", &start, &end);

    // 检查可达性
    checkReachability(&graph, start, end);

    return 0;
}

// 初始化图
void initGraph(struct Graph* graph, int vertices) {
    graph->vertices = vertices;

    // 初始化邻接矩阵
    for (int i = 0; i < vertices; i++) {
        for (int j = 0; j < vertices; j++) {
            graph->adjacencyMatrix[i][j] = 0;
        }
    }
}

// 添加边
void addEdge(struct Graph* graph, int start, int end) {
    // 有向图，将起始点到结束点的边标记为1
    graph->adjacencyMatrix[start][end] = 1;
}

// 深度优先搜索
void DFS(struct Graph* graph, int vertex, int visited[MAX_VERTICES]) {
    visited[vertex] = 1;
    printf("%d ", vertex);

    for (int i = 0; i < graph->vertices; i++) {
        if (graph->adjacencyMatrix[vertex][i] == 1 && !visited[i]) {
            DFS(graph, i, visited);
        }
    }
}

// 检查可达性
void checkReachability(struct Graph* graph, int start, int end) {
    int visited[MAX_VERTICES] = {0};

    printf("从顶点 %d 出发，DFS 遍历结果为：", start);
    DFS(graph, start, visited);

    if (visited[end]) {
        printf("\n%d 可达 %d\n", start, end);
    } else {
        printf("\n%d 不可达 %d\n", start, end);
    }
}