来自于深圳技术大学，此笔记涵盖了期末老师画的重点知识，分享给大家。
- 等深分箱和等宽分箱的区别：
- 等宽分箱基于数据的范围来划分箱子，每个箱子的宽度相等。
- 等深分箱基于数据的观测值数量来划分箱子，每个箱子包含相同数量的数据点。
文本编辑相似度度量方法
类比直角坐标系中两点距离，理解一下公式。
r 是一个正整数，称为参数或次数。当 r=1 时，明氏距离变为曼哈顿距离；当 r=2 时，它变为欧几里得距离。
曼哈顿距离是 单单每个类型的距离差之和。
X = (-3, -2, -1, 0, 1, 2,3) Y = (9, 4, 1, 0, 1, 4, 9)这个例子pearson的r是0 。
pearson=COV（x,y）/x的标准差*y的标准差。
*
最大最小值未知，或者离群点影响较大时
**
*
示例：
D
如果当某属性两个样例都为0对聚类的影响不大，例如医院体检两个人某种不重要的病毒抗原都是阴性，则不影响分到不同聚类。
这个时候abcd中的d就没啥用了。
通俗理解：jaccard=不一样的个数/（不一样的个数+都为1的个数）
jaccard数值小的越相似。
误差平方和不再减小
SSE（Sum of Squared Errors，误差平方和）是一种用于衡量聚类质量的指标。SSE计算的是每个数据点到其所属簇的中心的距离的平方之和。
kmeans算法还会受到，离群点，规模，形状，密度影响。
***
邻域：以样本为中心，eps为半径所包括的点
。
核心点：这个点的圈圈囊括的点的数量达到最小阈值 minpts
边界点：这个点的圈圈所囊括的点的数量未达到最小阈值 minpts，但是被核心点圈住了。
噪声点：既没有被核心点圈住，自己的圈圈里也没有达到最小阈值数量
直接密度可达：单个核心点它圈圈里的点，它可以直接可达的点。
密度可达：例如 A密度可达B （A必须是核心点） 意味着A可通过链接其他核心点最终到达B（B可以是核心点也可以是边界点）。密度可达是非对称的。
密度相连：跟密度可达唯一不同的是 A可以是边界点，即：A可通过链接其他核心点最终到达B
1.遍历数据集中的点，判断是否是核心，如果是创建簇，进行2，如果不是列为噪声点或边界点。
2.把核心点直接密度可达的点加入到簇中
3.循环，直到没有新的点添加到簇中
决策树
B站视频：http://【【数据挖掘】决策树零基础入门教程，手把手教你学决策树！】https://www.bilibili.com/video/BV1T7411b7DG?vd_source=1a684a3a1b9d05485b3d6277aeeb705d
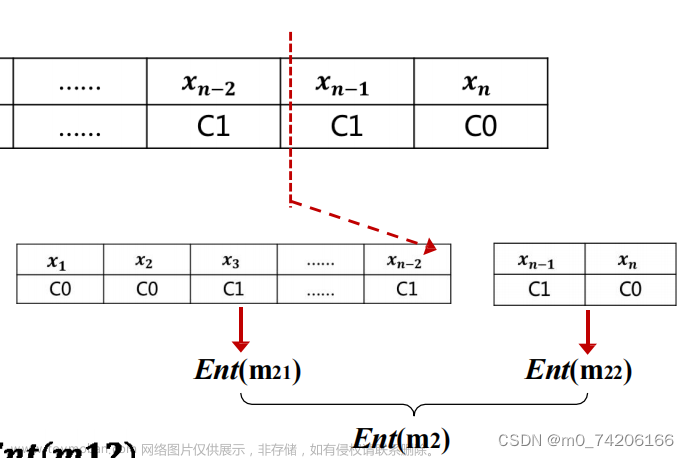
IG（X|Y）表示X在以Y为条件分为两类后，各类的加权熵比原来的熵减少了多少。
除了用熵来确定最优决策类别，还能用基尼系数来确定t。基尼系数是 1-所分的类别的平方和，一次分类好后要求加权基尼。
然后选择基尼系数最小的划分作为当前的最佳划分。
判断构建的决策树的优劣
判断构建的决策树的优劣
***
当d=1时就为一元线性回归。
=1289 8115
几何中心度
跟它相交的结点/除了自己以外的所有结点
接近中心度
下面的也不全对！
这里e11要*2
d1
分子in相当于自己社区内的边的和*2 ； tot是自己社区内的边的和*2+外部连接的边
文章来源：https://www.toymoban.com/news/detail-817988.html
在我的主页里搜索数据科学导论课件，可以获得期末总复习ppt，需要各章节ppt的私我。文章来源地址https://www.toymoban.com/news/detail-817988.html
到了这里，关于数据科学与大数据导论期末复习笔记（大数据）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
