假设你跟朋友通过打赌投篮来打赌一万块。你们找到一个篮球框,然后约定轮流投篮,谁先投进谁赢。假设你投进的概率是 p,也就是投不进的概率是 1-p,你对手投进的概率是 q,投不进的概率是 1-q,如果由你先投,那么你取胜的概率是多少。
在上面问题中我们把事情进行了理想化假设。也就是你和对手的准度不会变,不管你们投了 10 次还是 100 次,你们状态都保持一致,投入的概率永远不变。这个问题涉及到概率论中一个大类问题,那就是成功率为 p 的情况下,我们需要执行多少次试验才能获得第一次成功。要解决这个问题,我们首先需要了解几何不等式:
假设 |r| < 1,那么有: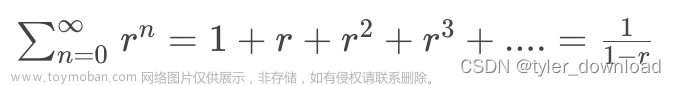
假设你在第 n 次投篮时,你投进获得了胜利,我们看基于 n 如何推导出取胜的规律来。如果 n=1,这意味着你第一次投就成功,对应的概率就是 p,如果 n=2,那意味着你投第一次不中概率为 1-p,然后对手投第一次同样不中,概率为 1-q,然后你投第二次结果中了,概率为 p,此时对应的概率就是(1-p)(1-q)p,如果我们这里用字符 r 替代(1-p)(1-q),那么对应概率就简化为 rp,如果 n=3,那说明你前两次不中,概率就是(1-p) ^ 2,对方前两次也不中,概率为(1-q) ^ 2,然后你第三次中了,于是概率就是(1-p) ^ 2 * (1-q) ^ 2 * p ,由于我们使用 r 代替(1-p)(1-q),因此(1-p) ^ 2 * (1-q) ^ 2 就可以简化为 r ^ 2,于是概率就是 r ^2 * p,由此我们就能推而广之,那就是当你在第 n 次投篮时成功对应的概率就是 r ^( n-1) * p。
由此我们就能推断,你在竞争中获胜的概率,那就是头一次就赢的概率加上投两次就赢的概率…,加上投 n 次就赢的概率,于是有:

注意这里的 r 是替代(1-p)(1-1)。于是我们用前面提供的公式就可以把上面式子简化为:
∑
n
=
0
∞
r
n
p
=
p
∑
n
=
0
∞
r
n
=
p
1
−
r
\sum_{n=0}^{\infin}r^{n}p=p\sum_{n=0}^{\infin}r^{n} =\frac{p}{1-r}
∑n=0∞rnp=p∑n=0∞rn=1−rp
事实上我们可以推导出上面的结论而不需要前面的几何级数公式。是想你第一次投篮就赢的概率是 p,如果你第一次不进,那么你要赢得比赛就需要对手第一次也不能进,此时你赢得概率没有变,就如同第一轮比赛没有发生过一样。如果使用 x 表示你赢的概率,那么 x 就等于你第一次投进的概率,加上你第一次不进,对方也第一次不进,然后乘以你赢的概率,也就是 x = p+(1-p)*(1-q)*x,如果我们把 x 解出来,那么就要 x = p / (1-r),可以看到我们第二种推导逻辑要比第一种简单和巧妙的多。
下面我们来点高级货,搞点微积分玩玩,这里的推导在后面的章节中会有大用处。有过高数学习经验的同学或许都了解过一个概念叫分部积分,要计算一个复杂的积分,我们需要把积分内的变量做各种代换才能计算出结果,我们看个例子,假设要计算如下积分,也就是公式(1):
我们需要做如下替换:
然后使用微分计算就有:
根据分部积分规则:
把上面步骤结合起来就有也就是公式(2):

由于:

由此公式(2)就转换为下面的公式(3):

同理我们再次实现分部积分处理公式(3)右边部分的积分,先做如下替换:
于是根据微分计算规则就有:

由此公式(3)就转换为下面的公式(4):
由于:

把上面推导代入公式(4),我们得到下面的公式(5):

这里注意到根据公式 1:

公式(5)就可以化简为下面的公式(6):

我们把变量 I 从公式(6)中解出来就有:
这样我们就解开了公式(1),于是就有如下公式(7):

至此我们解决了一个复杂微积分的计算问题,在这里我们也能体会到为何很少有人能在数学上有所积累,其实不在于它有多复杂而在于其过程的繁琐,在上面一系列步骤的引出中,只要有一步你没搞懂,那么后面推导就搞不懂,另外按下葫芦浮起瓢,你看到步骤 5,6 就会忘了步骤 3,4,因此需要我们反复琢磨才能把所有逻辑搞懂。当然付出肯定会有回报,有好的数学基础才能掌握复杂的大语言模型算法,或许爬山金字塔顶端并非路程有多难走,而是我们没有那个耐心持续走下去。文章来源:https://www.toymoban.com/news/detail-818181.html
更多精彩内容请在 B 站搜索 coding 迪斯尼。文章来源地址https://www.toymoban.com/news/detail-818181.html
到了这里,关于python 实现大语言模型中的概率论:两人轮流出手对决时取胜概率的推导的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




![概率论中的 50 个具有挑战性的问题 [第 6 部分]:Chuck-a-Luck](https://imgs.yssmx.com/Uploads/2024/02/767241-1.png)



