【算法日志】图论并查集及其简单应用-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法日志】图论并查集及其简单应用。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【算法日志】图论: 并查集及其简单应用

并查集概论

并查集是一种算法设计思想，通过判断两个元素是否在同一个集合里，常用来解决一些和图相关的连通性问题。

并查集主要有以下两个功能：

将两个元素添加到一个集合中。
判断两个元素是否是在一个集合之中(这一功能够有效判断是否成环)。

主要思想：

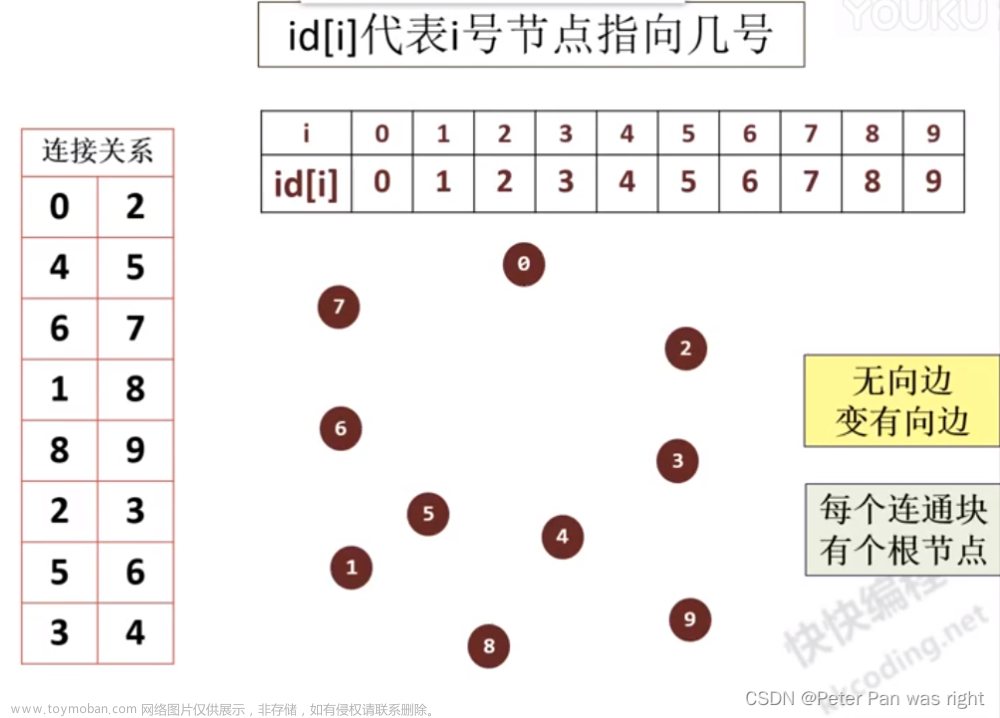
通过创建一个数组用来保每个点的最老根节点，以此来实现并查集的各种功能。

具体模板如下：

int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
int find(int u) {
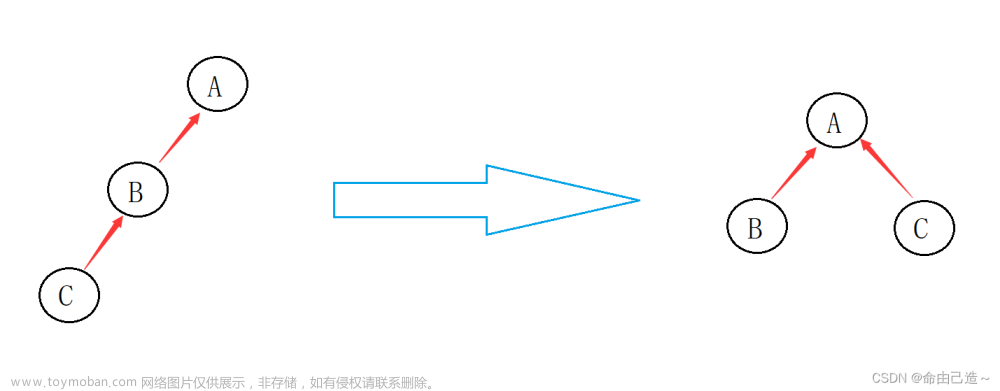
    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

简单应用

leetcode 1971:寻找是否存在路径

本题是双向图，只要始末点相连就存在有效路径，因此只需要将合并树，判断始末节点的最老根节点是否一样就行。

具体示例代码如下：文章来源地址https://www.toymoban.com/news/detail-818364.html

	void Init(vector<int>& f, const int& n)
	{
		for (int i = 0; i < n; ++i)
			f[i] = i;
	}
	int find(vector<int>& f, int v)
	{
		return v == f[v] ? v : find(f, f[v]);
	}
	bool isSame(vector<int>& f, int v, int u)
	{
		v = find(f, v);
		u = find(f, u);
		return v == u;
	}
	void join(vector<int>& f, int v, int u)
	{
		v = find(f, v);
		u = find(f, u);
		if (v != u)
			f[u] = v;
	}

	bool validPath(int n, vector<vector<int>>& edges, int source, int destination)
	{
		vector<vector<int>> path;
		vector<int> father(n + 1, 0);
		Init(father, n + 1);
		int size = edges.size();
		for (int i = 0; i < size; ++i)
			join(father, edges[i][0], edges[i][1]);
		return isSame(father, source, destination);
	}

leetcode 648: 冗余连接

本题要连接的点在连接前存在共同根节点，那么连接该两点就会形成环路，因此需要移除的边就是以这两点为端点的边。

具体示例代码如下：

	void Init(vector<int>& f, const int& n)
	{
		for (int i = 0; i < n; ++i)
			f[i] = i;
	}
	int find(vector<int>& f, int v)
	{
		return v == f[v] ? v : find(f, f[v]);
	}
	bool isSame(vector<int>& f, int v, int u)
	{
		v = find(f, v);
		u = find(f, u);
		return v == u;
	}
	void join(vector<int>& f, int v, int u)
	{
		v = find(f, v);
		u = find(f, u);
		if (v != u)
			f[u] = v;
	}
	vector<int> findRedundantConnection(vector<vector<int>>& edges)
	{
		int n = edges.size();
		vector<int> father(n + 1, 0);
		Init(father, n + 1);
		for (int i = 0; i < n; ++i)
		{
			if (isSame(father, edges[i][0], edges[i][1]))
				return { edges[i][0], edges[i][1] };
			join(father, edges[i][0], edges[i][1]);
		}
		return {};
	}

到了这里，关于【算法日志】图论并查集及其简单应用的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！