数据结构之栈的基本操作-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构之栈的基本操作。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

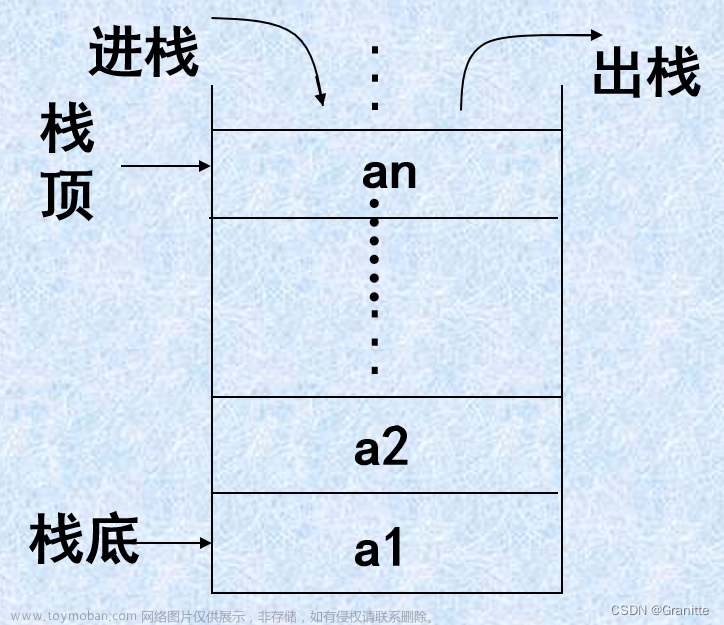
该顺序栈涉及到了存储整型数据的顺序栈还有存储字符型数据的顺序栈
实现的功能有：入栈、出栈、判断是否为空栈、求栈的长度、清空栈、销毁栈、得到栈顶元素
此外根据上述功能，编写了数值转换（十进制转化八进制）方法、括号匹配方法。

#include <stdio.h>
#include <stdlib.h>
#pragma warning(disable:4996)
#include<iostream>
using namespace std;
#define  STACK_INIT_SIZE  100
#define  STACKINCREMENT  10
#define OK 1
#define TRUE 1
#define FALSE 0
#define OVERFLOW 0
#define ERROR 0
 
typedef int Status;
typedef char SChar;
typedef int SElemType;
 
//定义栈，栈中存储的数据为整型数据 
typedef  struct
{
    SElemType* base;     //栈底指针
    SElemType* top;      //栈顶指针
    int  stacksize;            //当前已分配的存储空间
}SqStackInt, * SqslinkInt;      //顺序栈说明符
 
//定义栈，栈中存储的数据为字符型数据 
typedef  struct
{
    SChar* base;     //栈底指针
    SChar* top;      //栈顶指针
    int  stacksize;            //当前已分配的存储空间
}SqStackChar, * SqslinkChar;      //顺序栈说明符
 
 
//下面为 “栈中存储的数据为整型数据 ”的基本操作 
Status InitStackInt(SqStackInt& S) {
    //分配内存空间
    S.base = (SElemType*)malloc(STACK_INIT_SIZE * sizeof(SElemType));
    if (!S.base)exit(OVERFLOW);//分配失败
    S.top = S.base;
    S.stacksize = STACK_INIT_SIZE;//顺序栈最大的长度
    return OK;
}
//求顺序栈（整形数据）的长度
Status StackIntList(SqStackInt& S) {
    int list = (S.top - S.base);//栈的头指针减去尾指针就是长度
    printf("该顺序栈的长度为:%5d\n", list);
    return OK;
}
//清空顺序栈（整形数据）
Status ClearStackInt(SqStackInt& S) {
    S.top = S.base;
    printf("该整形顺序栈已经清空！");
    return OK;
}
//判断顺序栈（整形数据）是否为空栈
Status StackEmptyInt(SqStackInt S) {
    if (S.base == S.top) {
        printf("该整形顺序栈是空栈！");
        return TRUE;
    }
    else return FALSE;
}
//在顺序栈（整形数据）中得到栈顶元素
SElemType GetTop(SqStackInt& S, SElemType& e) {
    if (S.top == S.base) {
        return ERROR;
    }
    e = *(S.top - 1);//取出栈顶元素
    return OK;
}
//在顺序栈（整形数据）中进栈
Status PushInt(SqStackInt& S, SElemType e) {
    //判断栈是不是满了，如果满了就增加内存空间
    if (S.top - S.base >= S.stacksize) {
        S.base = (SElemType*)realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(SElemType));
        if (!S.base) exit(OVERFLOW);//realloc失败了
        S.top = S.base + S.stacksize;
        S.stacksize += STACKINCREMENT;
    }
    *S.top++ = e;
    return OK;
 
}
//在顺序栈（整形数据）中出栈
Status PopInt(SqStackInt& S, SElemType& e) {
    if (S.top == S.base) return ERROR;
    e = *--S.top;
   // printf("出栈的元素:%5d\n", e);
    int numer = e;
    return numer;
}
//销毁顺序栈（整形数据）
Status DestroyStackInt(SqStackInt& S) {
    S.stacksize = 0;//销毁后栈的长度为零
    S.top = S.base;
    free(S.base);//释放栈底
    S.top = S.base = NULL;
    printf("该顺序栈已被销毁");
    return OK;
}
 
 
//下面为 “栈中存储的数据为字符型数据 ”的基本操作 
Status InitStackChar(SqStackChar& S) {
    S.base = (SChar*)malloc(STACK_INIT_SIZE * sizeof(SChar));
    if (!S.base)exit(OVERFLOW);
    S.top = S.base;
    S.stacksize = STACK_INIT_SIZE;
    return OK;
}
 
Status ClearStackChar(SqStackChar& S) {
    S.top = S.base;
    return OK;
}
 
Status StackEmptyChar(SqStackChar S) {
    if (S.base == S.top) return TRUE;
    else return FALSE;
}
 
SChar GetTopChar(SqStackChar& S) {
    SChar e;
    if (S.top == S.base) return ERROR;
    e = *(S.top - 1);
    return e;
}
 
Status PushChar(SqStackChar& S, SChar e) {
    if (S.top - S.base >= S.stacksize) {
        S.base = (SChar*)realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(SChar));
        if (!S.base) exit(OVERFLOW);
        S.top = S.base + S.stacksize;
        S.stacksize += STACKINCREMENT;
    }
    *S.top++ = e;
 
    return OK;
}
 
SChar  PopChar(SqStackChar& S, SChar& e) {
    if (S.top == S.base) return ERROR;
    e = *--S.top;
    char data = e;
    return data;
}
 
 
Status DestroyStackChar(SqStackChar& S) {
    free(S.base);
    return OK;
}
 
//数制转换算法 
void conversion() {
    SqStackInt S;
    InitStackInt(S);
    int N;
    printf("请输入一个数:");
    scanf("%d", &N);
    while (N) {
        PushInt(S, N % 8);//如果N÷8的余数不为零就进栈
        N = N / 8;
    }
    SElemType e;
    while (!StackEmptyInt(S)) {
        PopInt(S, e);//所有余数出栈
        printf("%d", e);
    }
 
} // conversion
 
//括号匹配算法
Status  Matching()
{
    SqStackChar S;
    InitStackChar(S);
    int i =0; 
    char x; 
    ClearStackChar(S);
    SChar E[100];
    printf("请输入一组括号（以#结束）：");
    scanf("%s", &E);
    printf("你输入的是：%s\n", E);
    while (E[i] != '#')
    {
        if (E[i] == '(' || E[i] == '[') {
            PushChar(S, E[i]);   //（，[ 进栈
        }
        if (E[i] ==')' || E[i] == ']')
        {
            if (StackEmptyChar(S)) {
                return(ERROR);
            }//不匹配,返回0
            else {
                x = PopChar(S, E[i]);  //出栈，x为相应左括号
                if (x == '(' && E[i] == ']' || x == '[' && E[i] == ')') {                  
                    return(ERROR);
                }
            }    //不匹配返回0
        }
        i++;
       
    }
    if (StackEmptyChar(S))  return(OK);   //括号匹配，返回1
    else return(ERROR);  //不匹配返回0
 
}  //Matching
 
 
int main()
{
    SqStackInt int_S;
    InitStackInt(int_S);//初始化栈
    SElemType enterData_Int;//定义进栈的元素变量，对其赋值
    SElemType outData_Int;//元素出栈用此接受
    int n;//后面要进行的操做数，可以对其赋值
    SElemType e;//定义得到栈顶元素的变量
    int result;
    while (1)
    {
        printf("\n\n\n");
        printf("请从下面菜单中选择要操作的项：\n");
        printf("1、数制转换（十进制转换八进制）\n");
        printf("2、括号匹配\n");
        printf("3、整形数据元素进栈\n");
        printf("4、整形数据元素出栈\n");
        printf("5、求整形顺序栈的长度\n");
        printf("6、清空整形顺序栈\n");
        printf("7、销毁整形顺序栈\n");
        printf("8、判断整形顺序栈是否为空栈\n");
        printf("9、得到整形顺序栈的栈顶元素\n");
        printf("0、退出\n");
        printf("请输入1-9的数或者输入0结束程序:\n");
        scanf("%d", &n);
        switch (n) {
        case 1:
            conversion();
            break;
        case 2:
            result = Matching();
            if (result == OK)
                printf("括号匹配成功\n");
            else
                printf("括号匹配不成功\n");
            break;
        case 3:
            printf("请输入要进栈的整形数据元素:\n");
            scanf("%d", &enterData_Int);
            PushInt(int_S, enterData_Int);
            break;
        case 4:
           /* scanf("%d", &eOut);*/
            int num ;
            num= PopInt(int_S, outData_Int);
            printf("出栈的元素是:%5d\n", num);
           
            break;
        case 5:
            StackIntList(int_S);
            break;
        case 6:
            ClearStackInt(int_S);
            break;
        case 7:
            DestroyStackInt(int_S);
            break;
        case 8:
            StackEmptyInt(int_S);
            break;
        case 9:
            GetTop(int_S,e);
            break;
        case 0:
            exit(0);
            break;
        default:printf("输入数值错误，请重新输入\n"); break;
        }
    }
    return OK;
}