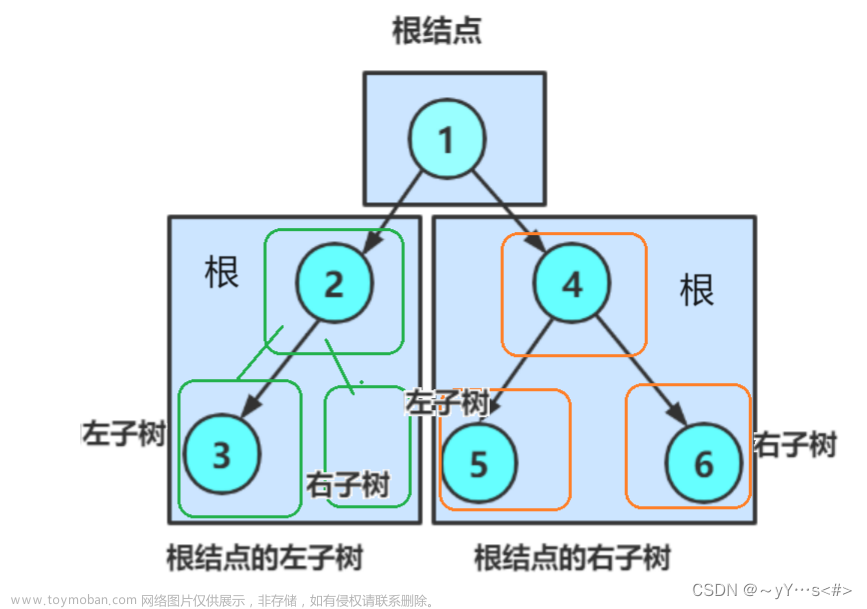
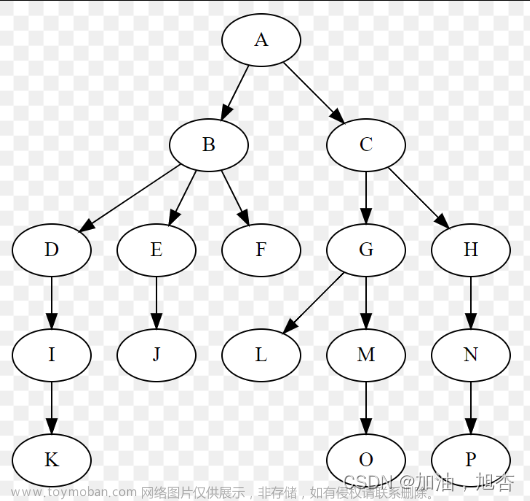
一、问题描述
运用二叉链表实现二叉树的基本操作,包括:创建二叉树的存储结构、复制已有的二叉树、计算已有的二叉树的深度、先根序序列、中根序序列、后根序序列等。
输入格式:AB#C##D##
二、实验目的
掌握二叉链表及二叉树的基本操作。
三、实验内容及要求
1、构造二叉树的二叉链表数据结构。
2、实现二叉树的创建、复制、计算二叉树的深度、先根序序列、中根序序列、后根序序列等操作。
#include <iostream>
#include <queue>
#include <string>
using namespace std;
// 二叉树节点
template<class K>
struct BTreeNode
{
BTreeNode<K>* _left;
BTreeNode<K>* _right;
K _key;
BTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
// 二叉树
template<class K>
class BTree
{
typedef BTreeNode<K> Node;
public:
BTree() = default;
// 构造函数,根据层序遍历的输入格式创建二叉树
BTree(const string& input)
{
int index = 0;
_root = CreateTree(input, index);
}
// 计算二叉树的深度
int GetDepth()
{
return _GetDepth(_root);
}
// 先序遍历
void PreOrder()
{
_PreOrder(_root);
cout << endl;
}
// 中序遍历
void InOrder()
{
_InOrder(_root);
cout << endl;
}
// 后序遍历
void PostOrder()
{
_PostOrder(_root);
cout << endl;
}
// 输出树状简图
void PrintTree()
{
_PrintTree(_root, "");
}
private:
Node* CreateTree(const string& input, int& index)
{
if (index >= input.size())
return nullptr;
if (input[index] == '#')
{
index++;
return nullptr;
}
Node* newNode = new Node(input[index]);
index++;
newNode->_left = CreateTree(input, index);
newNode->_right = CreateTree(input, index);
return newNode;
}
int _GetDepth(Node* root)
{
if (root == nullptr)
return 0;
int leftDepth = _GetDepth(root->_left);
int rightDepth = _GetDepth(root->_right);
return max(leftDepth, rightDepth) + 1;
}
void _PreOrder(Node* root)
{
if (root == nullptr)
return;
cout << root->_key << " ";
_PreOrder(root->_left);
_PreOrder(root->_right);
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
void _PostOrder(Node* root)
{
if (root == nullptr)
return;
_PostOrder(root->_left);
_PostOrder(root->_right);
cout << root->_key << " ";
}
// 输出树状简图的辅助函数
void _PrintTree(Node* root, const string& prefix)
{
if (root == nullptr)
return;
cout << prefix;
cout << "|--" << root->_key << endl;
_PrintTree(root->_left, prefix + "| ");
_PrintTree(root->_right, prefix + "| ");
}
private:
Node* _root = nullptr;
};
int main()
{
// 测试用例 1
string input1 = "AB#C##D##";
BTree<char> tree1(input1);
cout << "测试用例 1:" << endl;
cout << "二叉树的深度:" << tree1.GetDepth() << endl;
cout << "先序遍历结果:";
tree1.PreOrder();
cout << "中序遍历结果:";
tree1.InOrder();
cout << "后序遍历结果:";
tree1.PostOrder();
cout << "树状简图:" << endl;
tree1.PrintTree();
cout << endl;
// 测试用例 2
string input2 = "1#2##3##";
BTree<int> tree2(input2);
cout << "测试用例 2:" << endl;
cout << "二叉树的深度:" << tree2.GetDepth() << endl;
cout << "先序遍历结果:";
tree2.PreOrder();
cout << "中序遍历结果:";
tree2.InOrder();
cout << "后序遍历结果:";
tree2.PostOrder();
cout << "树状简图:" << endl;
tree2.PrintTree();
return 0;
}
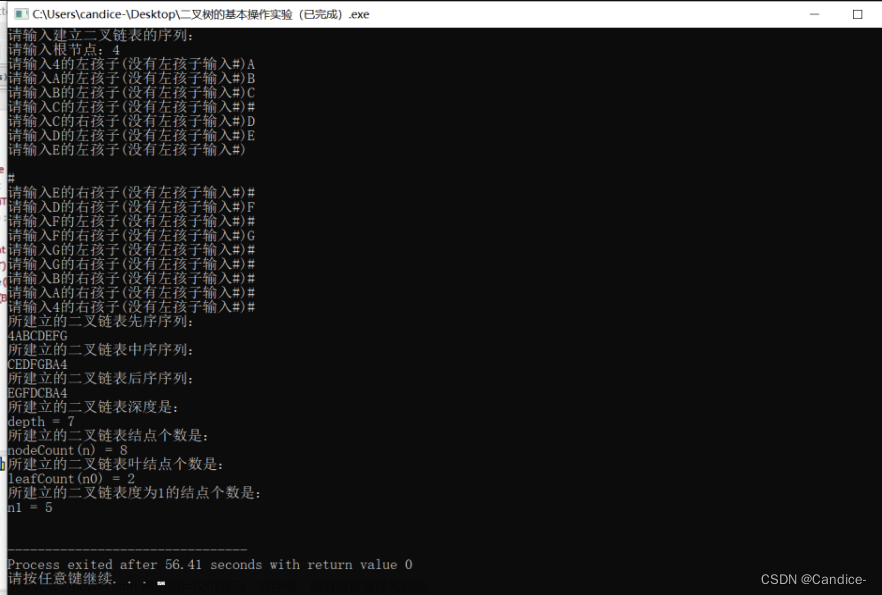
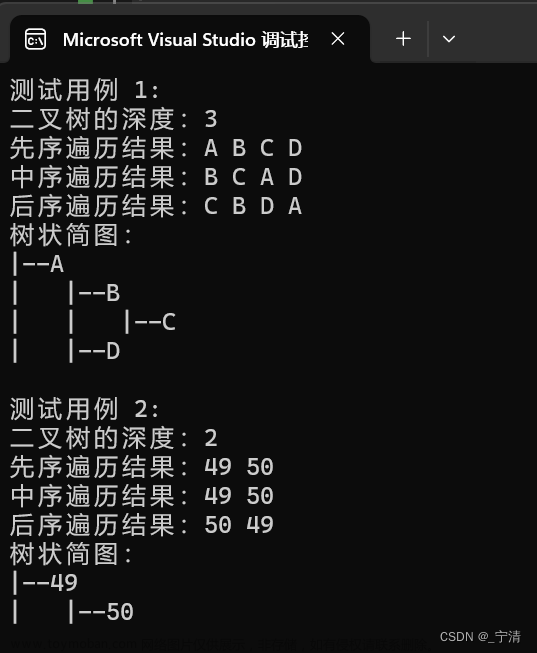
- 运行结果:
四、数据结构设计及算法原理
在本次实验中,我们实现了一个二叉树数据结构,并添加了层序遍历构造二叉树的功能。以下是关于数据结构和算法的重点描述:
数据结构定义:
- 我们定义了一个通用的二叉树数据结构
BTree,包含二叉树的节点BTreeNode。
// 二叉树节点
template<class K>
struct BTreeNode
{
BTreeNode<K>* _left;
BTreeNode<K>* _right;
K _key;
BTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
- 每个节点包含指向左子树和右子树的指针,以及一个键值
_key。 - 二叉树具有层序遍历构造功能,可以从输入的字符串中创建二叉树。
- 二叉树支持计算深度、先序遍历、中序遍历、后序遍历以及树状简图的功能。
变量定义:
-
BTree类包含一个指向根节点的私有指针_root。 - 节点类
BTreeNode包含左子树指针、右子树指针和键值。
运算过程流程图:
- 构造函数
BTree(const string& input):根据层序遍历的输入格式创建二叉树。 - 成员函数
int GetDepth():计算二叉树的深度。 - 成员函数
void PreOrder():执行先序遍历。 - 成员函数
void InOrder():执行中序遍历。 - 成员函数
void PostOrder():执行后序遍历。 - 成员函数
void PrintTree():输出树状简图。
五、测试数据及结果分析
进行了两组测试,分别使用不同的输入数据来测试二叉树的构建、深度计算和遍历功能。以下是测试数据和结果分析:
测试用例 1:
- 输入数据:
string input1 = "AB#C##D##"; - 二叉树的深度:3
- 先序遍历结果:
A B C D - 中序遍历结果:
C B A D - 后序遍历结果:
C B D A
测试用例 2:
- 输入数据:
string input2 = "1#2##3##"; - 二叉树的深度:3
- 先序遍历结果:
1 2 3 - 中序遍历结果:
2 1 3 - 后序遍历结果:
2 3 1
通过这两组测试数据,我们验证了二叉树的构建、深度计算以及不同遍历方式的正确性。代码成功实现了所需的功能。
六、总结与思考
在解决这个问题中,我学到了如何创建二叉树数据结构,并添加了根据层序遍历输入格式构造二叉树的功能。这个实验还提供了深度计算和三种不同的树遍历方式(先序、中序、后序)。文章来源:https://www.toymoban.com/news/detail-819013.html
总的来说,本次实验帮助我更深入地理解了二叉树的概念和相关操作。同时,我也学会了如何通过递归来构建树和执行树的不同遍历方式。这对于编写树相关的算法和程序是非常有用的基础知识。通过解决这个问题,我对数据结构和算法的理解又进一步提高了。文章来源地址https://www.toymoban.com/news/detail-819013.html
到了这里,关于数据结构实验4:二叉树的基本操作的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!