数据结构：搜索二叉树 | 平衡二叉树-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构：搜索二叉树 | 平衡二叉树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

博客写的代码都放在这里：gitee仓库链接

1.二叉搜索树

1.1.基本概念

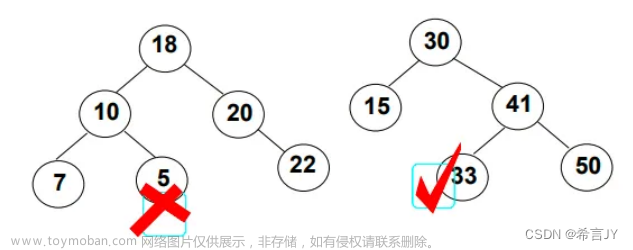
二叉搜索树又称二叉排序树，可以为空，如果不为空具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也都为二叉搜索树

数据结构：搜索二叉树 | 平衡二叉树,数据结构

1.2.二叉搜索树的结点结构

struct TreeNode
{
    TreeNode<T>* _left;
    TreeNode<T>* _right;
    T _key;

    TreeNode(T key)
        :_left(nullptr)
        , _right(nullptr)
        , _key(key)
    {}
};

1.3二叉搜索树的代码实现

1.二叉搜索树的插入

实现思路：

数据结构：搜索二叉树 | 平衡二叉树,数据结构

如果树为空，直接插入节点
如果树不为空，找到待插入位置（cur）的父节点（parent）
判断待插入的节点（cur）的值是否小于或大于父节点（parent）的值，插入对应的左边或右边

bool Insert(const T& key)

2.二叉搜索树的删除

实现思路：

删除的节点有两大类：1.没有子树或者只有一颗子树 2.有两颗子树

第一类的解决方式是：找到当前待删除的节点和其父节点，然后直接让父节点指向带待删除结点的子树（左子树和右子树）

数据结构：搜索二叉树 | 平衡二叉树,数据结构

把NULL也看成是一个特殊结点（最好的认识！）
分别删除4和14，让parent指向cur的子树（左或右，说明这里就需要判断了）；这里4的子树都是NULL，但是这里看成左子树和右子树都是可以的（只是我习惯从左往右）

第二类的解决方法是：使用替换法

数据结构：搜索二叉树 | 平衡二叉树,数据结构

找到一个结点和当前结点进行交换，怎么找一个符合的结点呢？将当前节点（cur）和左子树的最大节点（最右节点）或者右子树最小节点（最左节点）进行替换。
如这里删除3和8，找到leftMax说明已经是最右边的结点了！就让parent指向leftMax的左子树

bool Erase(const T& key);

1.4.二叉搜索树的性能

当二叉搜索树为完全二叉树，或者接近完成二叉树的时，它的插入或者说查找效率时log2(N)，但是但插入的数据有序或或者接近有序，那么就会退化成O(N)。数据结构：搜索二叉树 | 平衡二叉树,数据结构

所以，为了解决退化问题，可以使用平衡二叉树的红黑树来解决！

2.平衡二叉树

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查

找元素相当于在顺序表中搜索元素，效率低下。

当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度，搜索时间复杂度O(log2N)

平衡因子(bf) = 右子树的高度 - 左子树的高度

2.1平衡二叉树结点的定义

struct AVLTreeNode
{
    std::pair<K, V> _kv;
    AVLTreeNode<K,V>* _left;
    AVLTreeNode<K,V>* _right;
    AVLTreeNode<K,V>* _parent;
    int _bf;

    AVLTreeNode(const std::pair<K, V> kv)
        :_kv(kv)
        , _left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _bf(0)
    {}
};