目录
题目地址:
题目:
我们直接看题解吧:
快速理解解题思路小建议:
解题方法:
方法分析:
解题分析:
具体流程:
代码实现(递归):
补充说明:
解题思路(利用栈/队列):
具体流程:
题目地址:
226. 翻转二叉树 - 力扣(LeetCode)
难度:简单
今天刷翻转二叉树,大家有兴趣可以点上面链接,看看题目要求,试着做一下。
题目:
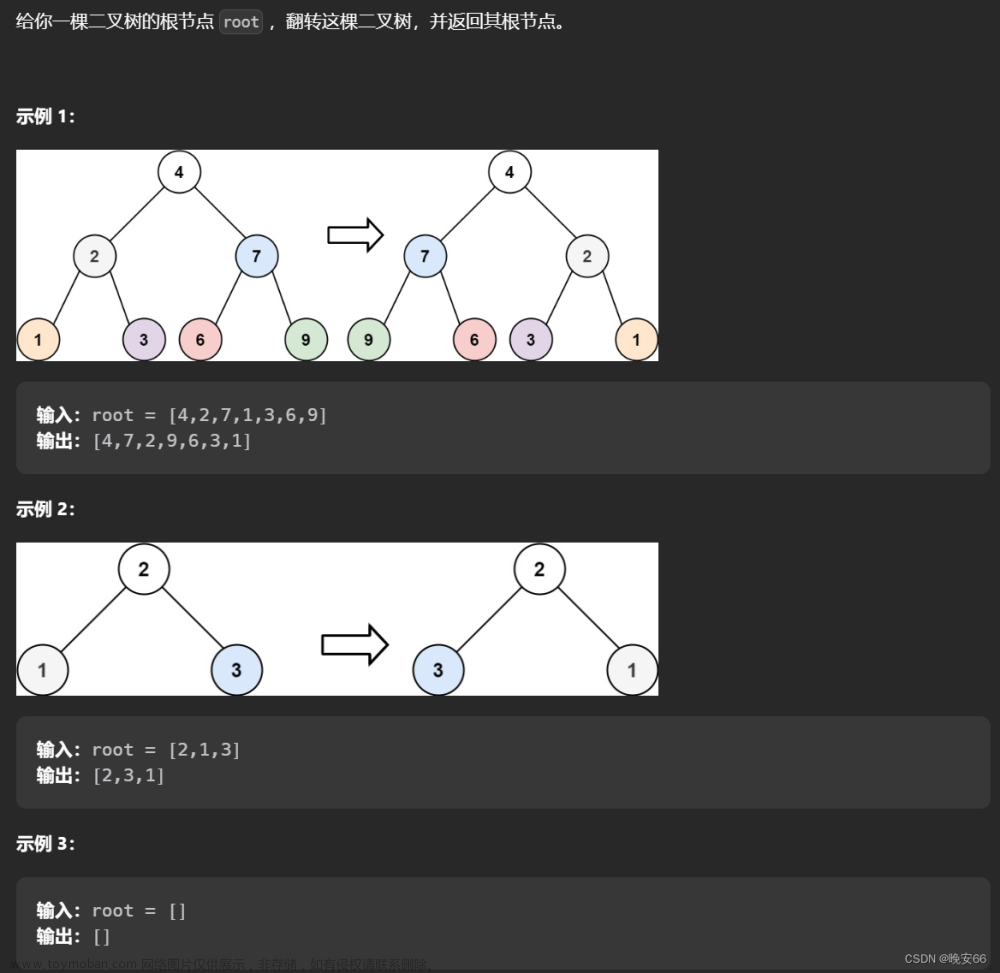
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。

我们直接看题解吧:
快速理解解题思路小建议:
可以先简单看一下解题思路,然后照着代码看思路,会更容易理解一些。
解题方法:
方法1递归
方法2利用栈/队列
方法分析:
实际上,递归相当于隐式栈/队列,方法2即为显式
解题分析:
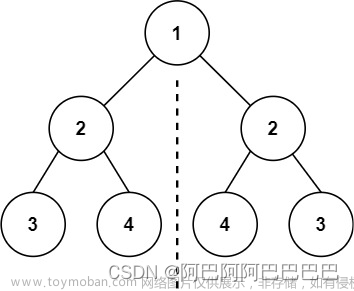
二叉树镜像定义:
对于二叉树中任意节点 root,设其左 / 右子节点分别为 left,right ;
则在二叉树的镜像中的对应 root 节点,其左 / 右子节点分别为 right,left 。
解题思路(递归):
我们从根节点开始,递归地对树进行遍历,并从叶子节点先开始翻转。
如果当前遍历到的节点 root的左右两棵子树都已经翻转,那么我们只需要交换两棵子树的位置,即可完成以 root 为根节点的整棵子树的翻转。
具体流程:
1、终止条件:当节点root为空(即越过叶子节点时),返回null
2、递归:
初始化临时节点tmp,用于临时存储root的左子节点。
递归右子节点,并将返回值作为root的左子节点
递归左子节点,并将返回值作为root的右子节点
3、最后返回当前节点root
可结合题解PDF进行理解--->226. 翻转二叉树 - 力扣(LeetCode)
代码实现(递归):
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return null;//当节点root为空(即越过叶子节点时),返回null
TreeNode tmp = root.left; //初始化临时节点tmp,用于临时存储root的左子节点。
root.left = invertTree(root.right);//递归右子节点,并将返回值作为root的左子节点
root.right = invertTree(tmp);//递归左子节点,并将返回值作为root的右子节点
return root;//最后返回当前节点root
}
}
补充说明:
1、由代码可知递归先遍历完整棵树的右子树遍历左左子树
2、为何序暂存root的左子节点?
在递归右子节点执行完后,root.left的值已发生改变,此时直接递归左子节点则会出问题
解题思路(利用栈/队列):
利用栈(或队列)遍历树的所有节点node,并交换每个 node 的左 / 右子节点。
具体流程:
1、 特殊处理:当root为空时,直接返回null
2、初始化:创建栈/队列,加入根节点
3、循环交换(当stack为空时跳出循环)
出栈:弹出节点赋值给节点node
添加子节点:将node节点的左右子节点压入栈
交换:利用临时节点tmp,对node的左右子节点进行交换
4、最后返回根节点root文章来源:https://www.toymoban.com/news/detail-819135.html
代码实现(利用栈/队列):文章来源地址https://www.toymoban.com/news/detail-819135.html
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return null;//当root为空时,直接返回null
Stack<TreeNode> stack = new Stack<>() {{ add(root); }};//创建栈/队列,加入根节点
while (!stack.isEmpty()) {//循环交换(当stack为空时跳出循环)
TreeNode node = stack.pop(); //弹出节点赋值给节点node
if (node.left != null) stack.add(node.left);//将node节点的左右子节点压入栈
if (node.right != null) stack.add(node.right);//将node节点的左右子节点压入栈
TreeNode tmp = node.left;
node.left = node.right;//利用临时节点tmp,对node的左右子节点进行交换
node.right = tmp;
}
return root;//返回根节点root
}
}
到了这里,关于翻转二叉树,力扣的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!