1. Toy模板网首页
  2. > Toy博客

动态规划之最长递增子序列

9月前 作者：Maravilloso 分类：Toy博客 阅读(43) 违法举报

这篇具有很好参考价值的文章主要介绍了动态规划之最长递增子序列。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

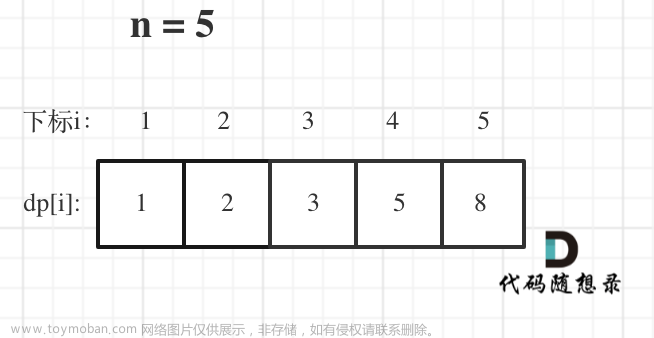
leetcode 300 最长递增子序列

1.定义dp数组：dp[i]表示以nums[i]结尾的最长递增子序列的长度。
2.定义递推公式
dp[i] = max(dp[j] + 1, dp[i]) 因为dp[j] + 1中的dp[j]并非是在前一个已经加1的dp[j]的基础之上再加上1。若从初始状态加1，而dp[i]永远保持的是最大的状态，则dp[j] + 1肯定要小一些。
3.初始化
Arrays.fill(dp, 1);
4.遍历顺序
for(int i = 0; i < nums.length; i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]){
dp[i] = max(dp[j] + 1, dp[i]) ;
}
}
}
5.最后再遍历一遍dp数组，返回其中的最大值。

    public int lengthOfLIS(int[] nums) {
        int res = 0;
        //定义dp数组
        int[] dp = new int[nums.length];
        //初始化dp数组
        Arrays.fill(dp, 1);
        //定义递推公式以及遍历顺序
        for(int i = 0; i < nums.length; i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[j] + 1, dp[i]);
                }
            }
            //每更新一次dp[i]的值便与以前一个nums[i]结尾的数组的最长递增子序列的值比较一次
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

leetcode 674 最长连续递增序列

1.定义dp数组：dp[i]是以i结尾的数列中的最长连续递增序列；
2.递推公式：本题只需考虑当前元素及其前一个元素；
dp[i] = dp[i - 1] + 1
3.初始化
Arrays.fill(dp, 1);
4.遍历顺序
只需要一层for循环，循环变量从1开始；
5.最后再遍历一遍dp数组，返回其最大值。

    public int findLengthOfLCIS(int[] nums) {
        //特判
        if(nums.length == 1){
            return 1;
        }
        int res = 0;
        //定义dp数组
        int[] dp = new int[nums.length];
        //初始化
        Arrays.fill(dp, 1);
        //递推公式以及遍历顺序
        for(int i = 1; i < nums.length; i++){
            if(nums[i] > nums[i - 1]){
                dp[i] = dp[i - 1] + 1;
            }
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}

leetcode 718 最长重复子数组

1.定义dp数组
dp[i][j]:表示以num1[i - 1]和nums2[j - 1]为尾部的数组num1和nums2的最长重复子数组的长度。
初始化：将无意义的值赋值为0：dp[i][0] = 0; dp[0][j] = 0;其余的值也为0。
2.递推公式
if(nums[i - 1] == nums[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}
3.遍历顺序
for(int i = 1; i <= nums1.length; i++){
for(int j = 1; j <= nums2.length; j++){
}
}
4.返回值
每遍历完dp数组的一个值，便与result进行一次比较，选出较大的值赋给result。

    public int findLength(int[] nums1, int[] nums2) {
        int res = 0;
        //定义dp数组
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        //初始化dp数组
        for(int i = 0; i <= nums1.length; i++){
            dp[i][0] = 0;
        }
        for(int j = 0; j <= nums2.length; j++){
            dp[0][j] = 0;
        }
        //定义递推公式以及遍历顺序
        for(int i = 1; i <= nums1.length; i++){
            for(int j = 1; j <= nums2.length; j++){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if(dp[i][j] > res){
                    res = dp[i][j];
                }
            }
        }
        return res;
    }
}

leetcode1143 最长公共子序列

本题与上一题的区别在于本题的公共子序列可以在两个数组中不连续。
1.定义dp数组
dp[i][j]表示nums1[0, i -1]与nums2[0, j - 1]两个数组中最长公共子序列的长度。
初始化：dp[i][0]与dp[0][j]的值没有意义，故初始化为0。
2.定义递推公式与遍历顺序
if(nums1[i - 1] == nums2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else{
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j -1]);
}
注意：dp数组的遍历顺序由递推公式的推导方向而得出。
3.最后返回dp[nums1.length][nums2.length]。

    public int longestCommonSubsequence(String text1, String text2) {
        //定义dp数组
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];
        //递推公式与遍历顺序
        for(int i = 1; i <= text1.length(); i++){
            for(int j = 1; j <= text2.length(); j++){
                if(text1.charAt(i - 1) == text2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.length()][text2.length()];
    }
}

leetcode 1035 不相交的线

本题的思路完全与上一题一致。

    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        //定义dp数组
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        //定义递推公式与遍历顺序：遍历顺序与递推公式的推导顺序有关
        for(int i = 1; i <= nums1.length; i++){
            for(int j = 1; j <= nums2.length; j++){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); 
                }
            }
        }
        return dp[nums1.length][nums2.length];
    }
}

leetcode 53 最大子序和

1.定义dp[i]:以nums[i]结尾的最大连续子序列的和。
2.递推公式
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);

public:
    int maxSubArray(vector<int>& nums) {
        int res = nums[0];
        //定义dp数组
        vector<int> dp(nums.size());
        //初始化dp数组
        dp[0] = nums[0];
        //定义递推公式以及遍历顺序
        for(int i = 1; i < nums.size(); i++){
            dp[i] = dp[i - 1] + nums[i] > nums[i] ? dp[i - 1] + nums[i] : nums[i];
            res = dp[i] > res ? dp[i] : res;
        }
        return res;
    }
};

leetcode 392 判断子序列

本题思路与1143最长公共子序列基本一致，只是本题仅仅考虑在更长的字符串t中删除元素以和s匹配最长公共子序列。
故唯一的区别在于递推公式：
if(s.charAt(i - 1) == t.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = dp[i][j - 1]
}

    public boolean isSubsequence(String s, String t) {
        if(s.length() > t.length()){
            return false;
        }
        //定义dp数组
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        //递推公式与遍历顺序
        for(int i = 1; i <= s.length(); i++){
            for(int j = 1; j <= t.length(); j++){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }
        if(dp[s.length()][t.length()] == s.length()){
            return true;
        }
        return false;
    }
}

leetcode115 不同的子序列

1.定义dp数组
dp[i][j]:表示以下标i - 1为结尾的字符串中拥有以下标j - 1为结尾的字符串作为子序列的个数。
2.递推公式以及初始化
if(s.charAt(i - 1) == t.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}else{
dp[i][j] = dp[i - 1][j];
}
初始化：
dp[i][0] = 1;表示一直删除字符串s中的元素，当s为空字符串时，恰好包含1个空字符串t。
dp[0][j] = 0;因为空字符串中一定不会包含非空字符串。
dp[0][0] = 1;因为空字符串中一定包含1个空字符串。
3.返回值
return dp[s.length()][t.length()];

    public int numDistinct(String s, String t) {
        //定义dp数组
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        //初始化
        for(int i = 0; i <= s.length();i++){
            dp[i][0] = 1;
        }
        //递推公式以及遍历顺序
        for(int i = 1; i <= s.length(); i++){
            for(int j = 1; j <= t.length(); j++){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }else{
                    dp[i][j] = dp[i - 1][j];//相当于从s中删除1个元素后，再看其中有多少个子序列t
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}

leetcode 583 两个字符串的删除操作

解法1：
1.定义dp数组：dp[i][j]表示使以i - 1下标结尾的字符串与以j - 1下标结尾的字符串相同所需要的最少的操作次数。
2.递推公式与初始化
if(s.charAt(i - 1) == t.charAt(j - 1))则dp[i][j] = dp[i - 1][j - 1];
否则的话：dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2);
初始化：dp[i][0] = i, dp[0][j] = j。
3.返回值：return dp[s.length()][t.length()]

    public int minDistance(String word1, String word2) {
        //定义dp数组
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        //初始化dp数组
        for(int i = 0; i <= word1.length(); i++){
            dp[i][0] = i;
        }
        for(int j = 0; j <= word2.length(); j++){
            dp[0][j] = j;
        }
        //递推公式以及遍历顺序
        for(int i = 1; i <= word1.length(); i++){
            for(int j = 1; j <= word2.length(); j++){
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1];//若对应下标位置处的字母相等，则将其去除与否均不影响最小操作次数
                }else{
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 2);
                }
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

解法2：
可以先求出两个字符串的最长公共子序列的长度，再s.length() + t.length() - 2 * 最长公共子序列的长度。

    public int minDistance(String word1, String word2) {
        //定义dp数组
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        //递推公式以及遍历顺序
        for(int i = 1; i <= word1.length(); i++){
            for(int j = 1; j <= word2.length(); j++){
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return word1.length() + word2.length() - 2 * dp[word1.length()][word2.length()];
    }
}

leetcode 72 编辑距离

1.定义dp数组
dp[i][j]表示使以下标i - 1位置结尾的字符串与以下标j - 1位置结尾的字符串相同的话所需要的最小操作次数。
2.递推公式以及遍历顺序
if(s.charAt(i - 1) == t.charAt(j - 1))则将对应位置的字母去掉与否都不会影响最终的最少操作次数，故dp[i][j] = dp[i - 1][j - 1];
否则，dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 1);
因为将s的最后一个字母去掉后，其本身便对应1次操作；同理将t的最后一个字母去掉后也对应1次操作，或者将s与t其中之一的最后一个字母替换为另一个的字母而使其相同。
注意：删除操作和增添操作是一一对应的关系，故它们的操作次数一样，所以只需要递推其中之一即可。
3.初始化
dp[i][0] = i; dp[0][j] = j （这里可以将下标0理解为空字符串）
4.返回值
return dp[s.length()][t.length()] (因为这对应完整长度的s与t的最少操作次数)

    public int minDistance(String word1, String word2) {
        //定义dp数组
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        //初始化dp数组
        for(int i = 0; i <= word1.length(); i++){
            dp[i][0] = i;
        }
        for(int j = 0; j <= word2.length(); j++){
            dp[0][j] = j;
        }
        //递推公式与遍历顺序
        for(int i = 1; i <= word1.length(); i++){
            for(int j = 1; j <= word2.length(); j++){
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1];
                }else{
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 1);
                }
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

leetcode 647 回文子串

1.定义dp数组：dp[i][j]表示子串[i, j]是否是回文子串，是则记录true，否则记录false。
2.定义递推公式：
if(s.charAt(i) == s.charAt(j)),且j - i <= 1，则一定是回文子串。此时，result++;
若在此前提下，j - i > 1,则继续判断s.charAt(i + 1)是否等于s.charAt(j - 1)，若是，则[i, j]是回文子串，dp[i][j]为true, result++。
3.定义遍历顺序
根据递推公式的推导顺序，遍历顺序应该是从下往上，从左往右。
for(int i = s.length() - 1; i >= 0; i–){
for(int j = i; j < s.length(); j++){}
}

    public int countSubstrings(String s) {
        int result = 0;
        //定义dp数组,默认初始化为false
        boolean[][] dp = new boolean[s.length()][s.length()];
        //定义递推公式以及遍历顺序,j始终大于等于i
        for(int i = s.length() - 1; i >= 0; i--){
            for(int j = i; j < s.length(); j++){
                if(s.charAt(i) == s.charAt(j)){
                    if(j - i <= 1){
                        dp[i][j] = true;
                        result++;
                    }else{
                        if(dp[i + 1][j - 1] == true){
                            dp[i][j] = true;
                            result++;
                        }
                    }
                }
            }
        }
        return result;
    }
}

leetcode 516 最长回文子串

本题与上一题的区别在于其回文子序列可以不连续。
1.定义dp数组：dp[i][j]表示子序列[i, j]的最长回文子串（可以不连续）的长度。
2.定义递推公式以及遍历顺序
if(s.charAt(i) == s.charAt(j))，则dp[i][j] = dp[i + 1][j - 1] + 2;
若上述条件不相等，则dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);其分别表示只考虑字符串的左边或只考虑字符串的右边，选出两者最大的。
遍历顺序根据递推公式是从下往上，从左到右。
for(int i = s.length() - 1; i >= 0; i–){
for(int j = i + 1; j < s.length(); j++){}//j必须从i + 1开始，才能保证[i, j]子序列的长度至少为2。因为dp[i][i]已经被初始化为1了。
}
3.最后返回dp[0][s.length() - 1]。文章来源地址https://www.toymoban.com/news/detail-819445.html

    public int longestPalindromeSubseq(String s) {
        //定义dp数组
        int[][] dp = new int[s.length()][s.length()];
        //初始化dp数组
        for(int i = 0; i < s.length(); i++){
            dp[i][i] = 1;//只有1个字符的子序列也是长度为1的回文子序列
        }
        //定义递推公式以及遍历顺序
        for(int i = s.length() - 1; i >= 0; i--){
            for(int j = i + 1; j < s.length(); j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }else{
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
                }
            }
        }
        return dp[0][s.length() - 1];
    }
}

到了这里，关于动态规划之最长递增子序列的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 代码随想录 动态规划-基础题目

    代码随想录 动态规划-基础题目

    目录 509.斐波那契数  70.爬楼梯 746.使用最小花费爬楼梯 62.不同路径 63.不同路径|| 343.整数拆分 96.不同的二叉树 509. 斐波那契数 简单 斐波那契数  （通常用  F(n)  表示）形成的序列称为  斐波那契数列  。该数列由  0  和  1  开始，后面的每一项数字都是前面两项数字的和

    2024年03月18日
    浏览(74)
  • 动态规划例题（代码随想录学习）——持续更新

    动态规划例题（代码随想录学习）——持续更新

    dp[i][j]的含义是：从（0，0）到（i，j）的不同路径 当路线中有了障碍，此路不通，所以在不同路径的递推公式上需要增加条件 if（obs[i,j]==0）没有障碍，dp[i][j]= dp[i-1][j]+dp[i][j-1] if（obs[i][j]==1）有障碍，不进行推导 obs数组表示障碍 障碍的后面应该是0（原因：遇到障碍后，即

    2024年04月12日
    浏览(43)

  • 二刷代码随想录——动态规划day40

    一个本硕双非的小菜鸡，备战24年秋招，计划二刷完卡子哥的刷题计划，加油！ 二刷决定精刷了，于是参加了卡子哥的刷题班，训练营为期60天，我一定能坚持下去，迎来两个月后的脱变的，加油！ 推荐一手卡子哥的刷题网站，感谢卡子哥。代码随想录 终于来到了守关boss。

    2024年03月11日
    浏览(55)
  • 代码随想录第41天 | 动态规划part03

    代码随想录第41天 | 动态规划part03

    ● 343. 整数拆分 ● 96.不同的二叉搜索树 题目一 343. 整数拆分 给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。 示例 : 输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。 说明: 你可以假设 n 不小于 2 且不大于 5

    2024年01月24日
    浏览(50)
  • 动态规划01背包问题-代码随想录-刷题笔记

    动态规划01背包问题-代码随想录-刷题笔记

    有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。 每件物品只能用一次 ，求解将哪些物品装入背包里物品价值总和最大。 二维dp数组01背包 确定dp数组以及下标的含义 是使用二维数组，即 dp[i][j] 表示从下标为[0-i]的物品里任意取，

    2024年02月07日
    浏览(56)

  • 代码随想录算法训练51 | 动态规划part12

    本题加了一个冷冻期，状态就多了，有点难度，大家要把各个状态分清，思路才能清晰  视频讲解： 动态规划来决定最佳时机，这次有冷冻期！| LeetCode：309.买卖股票的最佳时机含冷冻期_哔哩哔哩_bilibili 代码随想录 相对122.买卖股票的最佳时机II ，本题只需要在计算卖出操

    2024年01月18日
    浏览(54)
  • 代码随想录Day41：动态规划Part3

    代码随想录Day41：动态规划Part3

    讲解前： 毫无头绪 讲解后： 这道题的动态思路一开始很不容易想出来，虽然dp数组的定义如果知道是动态规划的话估摸着可以想出来那就是很straight forward dp定义：一维数组dp[i], i 代表整数的值，dp[i] 代表将整数 i 拆分的话可以获得的最大乘积 然后呢就是定义递归推导式了，

    2024年04月27日
    浏览(41)
  • 【每日刷题】动态规划-代码随想录动规-8、9

    【每日刷题】动态规划-代码随想录动规-8、9

    题目链接 dp数组含义 ：dp[i]表示拆分i的最大乘积 递推公式 ：dp[i]= max(j*(i-j), j*dp[i-j], dp[i]) 解释：从1遍历j，有两种渠道得到dp[i]. 一个是j * (i - j) 直接相乘。 一个是j * dp[i - j]，相当于是拆分(i - j) 为何不拆分j：j是从1开始遍历，拆分j的情况，在遍历j的过程中其实都计算过了

    2024年02月02日
    浏览(48)
  • 【代码随想录】Day 49 动态规划10 （买卖股票Ⅰ、Ⅱ）

    【代码随想录】Day 49 动态规划10 （买卖股票Ⅰ、Ⅱ）

    https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/ dp[i]表示在第i天时，卖/不卖股票能获得的最大利润： 1、卖股票：dp[i] = prices[i] -minPrice（i天以前的最低价格） 2、不卖股票：dp[i] = dp[i-1]（因为不卖股票，所以状态和前一天保持一致） ∴dp[i] = max(dp[i-1], prices[i] - minPrice)； https

    2024年02月09日
    浏览(43)

  • Day39 代码随想录(1刷) 动态规划 0-1背包

    题目描述 小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的空间，并且具有不同的价值。  小明的行李空间

    2024年04月23日
    浏览(51)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包