麻省理工学院 - MIT - 线性代数（我愿称之为线性代数教程天花板）_哔哩哔哩_bilibili
MIT—线性代数笔记00 - 知乎 (zhihu.com)
一、求解Ax=0
计算零空间
矩阵A的零空间即满足Ax=0的所有x构成的向量空间。
取 (A的列向量并不线性无关)
对于矩阵A进行“行操作”并不会改变Ax=b的解，因此也不会改变零空间。（但是会改变列空间。）此处不需要应用增广矩阵，因为等号右侧的向量b=0。
矩阵的秩（rank）就是矩阵的主元的个数。本例中矩阵A和U的秩均为2。矩阵中包含主元的列为主元列（pivot column），不包含主元的列称为自由列（free column）。
特解
当我们将系数矩阵变换为上三角阵U时，就可以用回代求得方程Ux=0的解。本例中，包含主元的矩阵第1列和第3列为主元列，而不包含主元的第2列和第4列为自由列。
对自由变量（free variable）x2和x4我们可以进行赋值。例如令x2=1而x4=0。
因此可得一解，其任意倍数均在矩阵的零空间之内；
取自由变量中x2=0而x4=1，则可得到另一解
矩阵A的零空间就是这些“特解”向量的线性组合所构成的向量空间。（有多少个特解？取决于有多少个自由变量）
为社么给自由变量分配值取0,1、1,0?
答：选别的也可以，但我们要求的是零空间，取其他数也是这两个向量的线性组合
矩阵的秩r 等于其主元列的数目，因此自由列的数目就等于n-r，即列的数目减去主元列的数目。这个数值等于特解的数目和零空间的维数。
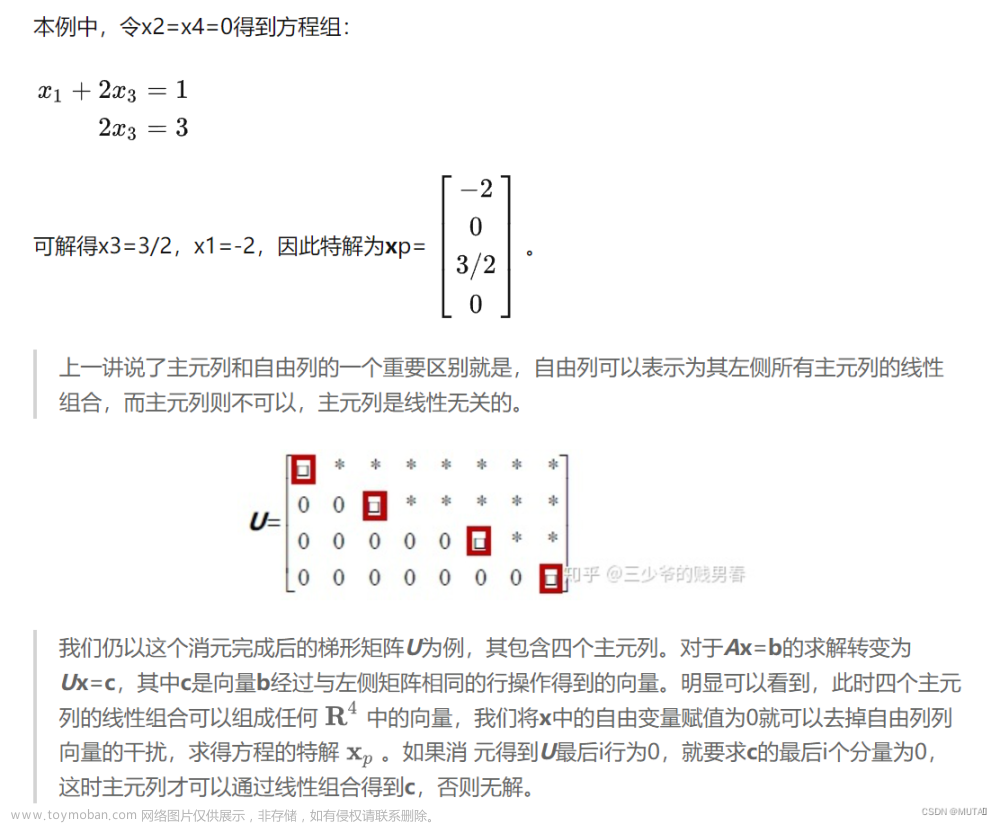
主元列和自由列的一个重要区别就是，自由列可以表示为其左侧所有主元列的线性组合，而主元列则不可以。
行最简阶梯矩阵
这里的I 是一个rxr的方阵。F 即自由列消元后组成的部分。
原方程Ax=0变为求解R的主元行乘以x，。
我们将Ax=0的特解作为列向量写成一个矩阵N，即零空间矩阵，其形式为，这里的T为(n-r)*(n-r)的矩阵，就是把n-r个自由变量分别赋值为1构造出来的；又因为零空间矩阵满足RN=0，分块运算可知最终.
对于矩阵R 而言，求零空间特解就变得非常简单，只需要将消元的到的F 部分拼接上单位阵就可以得到所有的通解。注意如果在变换出R 左上角的单位阵的过程中采用了列交换，则最后的解要完成逆变换。
二、求解Ax=b
可解的条件
检验Ax=b是否可解的方法是对增广矩阵进行行消元。如果矩阵A的行被完全消去的话，则对应的b的分量也要得0。
之前讨论过，只有当b处于矩阵的列空间C(A)之中时，方程才有解。这里推导出矩阵A的行向量若经过线性组合成为了零向量，则对应的b经同样的线性组合后也要等于0。因此看起来我们有了两条关于b的限制条件，但实际上这两点是等价的。
特解
求Ax=b特解的方法是将自由变量均赋值为0，求解其主变量。
通解
为求得Ax=b的所有解，我们首先检验方程是否可解，然后找到一个特解。将特解和矩阵零空间的向量相加即为方程的通解。
矩阵的零空间N(A)是R4空间中的二维子空间，方程的解Ax=b构成了穿过xp点并和矩阵零空间平行的“平面“。但该”平面“并不是R4空间的子空间。
秩
三、线性无关、基、维数
线性无关
矩阵A为mxn矩阵，其中m<n（因此Ax=b中未知数个数多于方程数）。则A中具有至少一个自由变量，那么Ax=0一定具有非零解。A的列向量可以线性组合得到零向量，所以A的列向量是线性相关的。
- 若 c1x1+c2x2+⋯+cnxn=0 仅在c1=c2=⋯=cn=0 时才成立，则称向量x1，x2……xn是线性无关的。若这些向量作为列向量构成矩阵A，则方程Ax=0只有零解x=0，或称矩阵A的零空间只有零向量。换而言之，若存在非零向量c，使得Ac=0，则这个矩阵A的列向量线性相关。
在R2空间中，两个向量只要不在一条直线上就是线性无关的。（在R3中，三个向量线性无关的条件是它们不在一个平面上。）
如果矩阵A的列向量为线性无关，则A所有的列均为主元列，没有自由列，矩阵的秩为n。若A的列向量为线性相关，则矩阵的秩小于n，并且存在自由列。
张成空间
当一个空间是由向量v1，v2……vk的所有线性组合组成时，我们称这些向量张成了这个空间。例如矩阵的列向量张成了该矩阵的列空间。
如果向量v1，v2……vk张成空间S，则S是包含这些向量的最小空间。
基
向量空间的基是具有如下两个性质的一组向量v1，v2……vd：
- v1，v2……vd 线性无关
- v1，v2……vd张成该向量空间
向量，可以张成R3中的一个平面，但是它们无法成为R3空间的一组基。
维数
空间的每一组基都具有相同的向量数，这个数值就是空间的维数（dimension）。所以Rn空间的每组基都包含n个向量。
列空间的基和维数
取
讨论列空间：矩阵A的四个列向量张成了矩阵A的列空间，其中第3列和第4列与前两列线性相关，而前两个列向量线性无关。因此前两列为主元列。他们组成了列空间C(A)的一组基。矩阵的秩为2。
零空间的基和维数
本例中矩阵的列向量不是线性无关的，因此其零空间N(A)不止包含零向量。因为可以看出第3列是第1列和第2列的加和。所以向量必然在零空间N(A)之内。同样还可以对x4赋值为1，从而得到也在零空间之内。它们就是Ax=0的两个特解。
这两个特解就构成了零空间的一组基。
实际上对于任何矩阵A均有：
矩阵的秩r=矩阵主元列的数目=列空间的维数
零空间的维数=自由变量数目=n-r
四、四个基本子空间
任意的mxn矩阵A都定义了四个子空间。
列空间C(A)
矩阵A的列空间是A的列向量的线性组合在 空间中构成的子空间。
矩阵A的r个主元列构成了列空间C(A)的一组基。dim C(A)=r
零空间 N(A)
矩阵A的零空间是Ax=0的所有解x在空间中构成的子空间。
Ax=0的一组特解对应于矩阵A的n-r个自由列，并构成了零空间的一组基。dim N(A)=n-r
行空间 C( )
矩阵A的行空间是A的行向量的线性组合在Rn空间中构成的子空间，也就是矩阵的列空间。
我们用矩阵A的化简的行阶梯矩阵R。
尽管矩阵A和矩阵R的列空间不同，但两者行空间相同。R的行向量来自于A的行向量的线性组合，因为消元操作是可逆的，所以A的向量也可以表示为R行向量的线性组合。
R的前r行阶梯型“行向量”就是矩阵A行空间C( )的一组基。dim C( )=r
左零空间N( )
我们称矩阵 的零空间为矩阵A的左零空间，它是空间中的子空间。
左零矩阵是满足 y=0 的所有向量y的集合。称之为左零矩阵是因为该式可写作A=0，而y出现在矩阵A左侧。
五、正交向量与正交子空间
正交向量
正交就是垂直（perpendicular）的另一种说法。两向量正交的判据之一是其点积
零向量与所有向量都正交。
正交子空间
子空间S与子空间T正交，则S中的任意一个向量都和T中的任意向量正交。
注意：黑板所在的平面和地板所在平面不是正交关系，沿两者的交线方向的向量同时属于两个平面，但并不与自己正交。
零空间与行空间正交
行空间和零空间实际上把Rn空间分割成了两个正交的子空间
,其行空间是1维的，向量 是它的基向量，而其零空间是垂直于并穿过原点的2维平面。
空间和零空间不仅仅是正交，并且其维数之和等于n，我们称行空间和零空间为Rn空间内的正交补（orthogonal complements）。这表示零空间包含所有和行空间正交的向量，反之亦然。
矩阵
如何求解无解方程组Ax=b的解？
A是m×n，m>n的系数矩阵，m>n表示左侧方程式多，容易混进坏数据，这时候线性代数要做的是在这种条件下求一个最优解
矩阵发挥重要作用，它是n×n矩阵，
矩阵发挥重要作用，它是n×n矩阵，并且对称，
实际上 ，并且矩阵的秩等于A的秩
因此矩阵可逆，要求A的零空间只有零向量，即A的列向量线性无关
文章来源地址https://www.toymoban.com/news/detail-819625.html文章来源：https://www.toymoban.com/news/detail-819625.html
到了这里，关于线性代数——理解向（2）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
