一开始想到的方法非常低效,但好理解。
思路分析:
-
使用二维数组
dp来记录递增子序列的长度信息,其中dp[i][0]表示以nums[i]结尾的最长递增子序列的长度,dp[i][1]表示包含nums[i]的最长递增子序列的长度。 -
初始化
dp数组,将以第一个元素结尾的递增子序列长度置为0。 -
使用两层循环遍历数组,比较当前元素与前面元素的大小关系,更新
dp数组的值。 -
最终返回最后一个元素的两种状态中的最大值,即为整个数组的最长递增子序列的长度。
这种动态规划算法的时间复杂度为O(n^2),其中n为数组的长度。
class Solution {
public:
// 函数用于计算最长递增子序列的长度
int lengthOfLIS(vector<int>& nums) {
// dp[i][0]表示以nums[i]结尾的最长递增子序列的长度
// dp[i][1]表示包含nums[i]的最长递增子序列的长度
vector<vector<int>> dp(nums.size(), vector<int>(2, 1));
// 初始化dp数组,将以第一个元素结尾的递增子序列长度置为0
dp[0][0] = 0;
// 遍历数组,计算dp数组的值
for (int i = 1; i < nums.size(); i++) {
for (int j = i - 1; j >= 0; j--) {
// 如果当前元素大于前面的某个元素,更新包含当前元素的递增子序列的长度
if (nums[i] > nums[j]) {
dp[i][1] = max(dp[i][1], dp[j][1] + 1);
}
// 更新以当前元素结尾的递增子序列的长度
dp[i][0] = max(dp[i][0], max(dp[j][1], dp[j][0]));
}
}
// 返回最终结果,取最后一个元素的两种状态中的最大值
return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);
}
};但还有种既节省空间也节省时间的方法。
思路分析:
-
初始化dp数组,其中
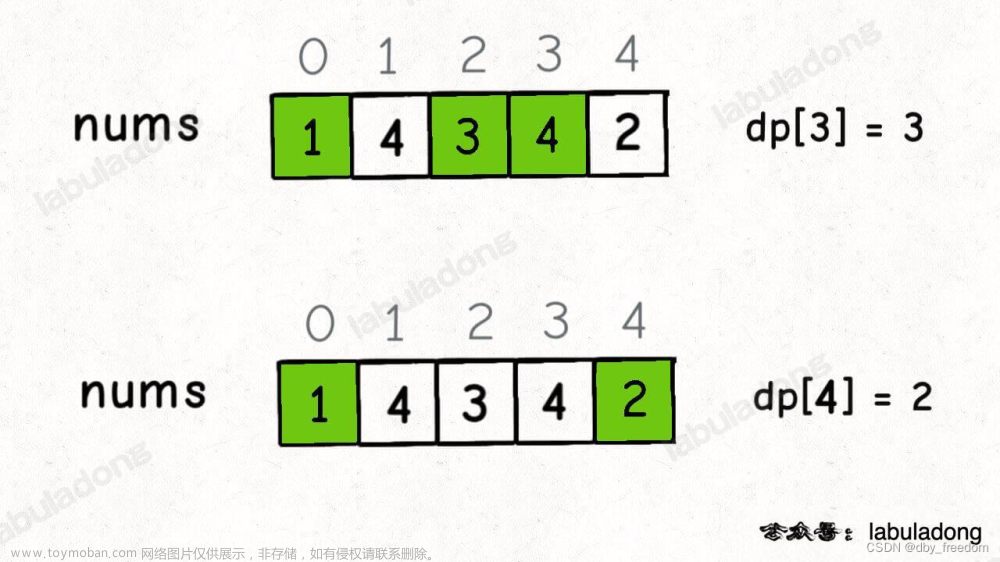
dp[i]表示以第i个元素结尾的最长递增子序列的长度,初始值为1。 -
使用两层循环遍历数组,对于每个元素,查找在其之前的元素中比它小的元素,更新以当前元素结尾的最长递增子序列的长度。
-
在内循环中,通过比较当前元素与之前元素的大小关系,更新
dp数组的值。 -
同时,记录整个数组的最长递增子序列的长度,即取
dp数组中的最大值。 -
最终返回整个数组的最长递增子序列的长度。文章来源:https://www.toymoban.com/news/detail-819627.html
这种算法的时间复杂度为O(n^2),其中n为数组的长度。文章来源地址https://www.toymoban.com/news/detail-819627.html
class Solution {
public:
// 函数用于计算最长递增子序列的长度
int lengthOfLIS(vector<int>& nums) {
// 如果数组长度小于等于1,直接返回数组长度
if (nums.size() <= 1) return nums.size();
// dp数组用于记录以每个元素结尾的最长递增子序列的长度
vector<int> dp(nums.size(), 1);
// result用于记录整个数组的最长递增子序列的长度
int result = 0;
// 遍历数组
for (int i = 1; i < nums.size(); i++) {
// 在当前元素之前的元素中查找比当前元素小的元素
for (int j = 0; j < i; j++) {
// 如果找到比当前元素小的元素,更新以当前元素结尾的最长递增子序列的长度
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
// 更新整个数组的最长递增子序列的长度
if (dp[i] > result) {
result = dp[i];
}
}
// 返回最终结果,即整个数组的最长递增子序列的长度
return result;
}
};到了这里,关于力扣--动态规划300.最长递增子序列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!