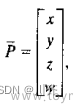[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-3(3) 刚体的位形 Configuration of Rigid Body-Toy模板网

这篇具有很好参考价值的文章主要介绍了[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-3(3) 刚体的位形 Configuration of Rigid Body。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文仅供学习使用，总结很多本现有讲述运动学或动力学书籍后的总结，从矢量的角度进行分析，方法比较传统，但更易理解，并且现有的看似抽象方法，两者本质上并无不同。

2024年底本人学位论文发表后方可摘抄
若有帮助请引用
本文参考：
.

食用方法
如何表达刚体在空间中的位置与姿态
姿态参数如何表达？不同表达方式直接的转换关系？
旋转矩阵？转换矩阵？有什么意义和性质？转置代表什么？
如何表示连续变换？——与RPY有关
齐次坐标的意义——简化公式？
务必自己推导全部公式，并理解每个符号的含义

3.8 点、线、面、向量在坐标系下的表达

对于固定坐标系下同一点/向量，在不同坐标系 $\left\{ A \right\} ,\left\{ B \right\}$ 下进行表达，存在如下转换关系：
$\vec{R}_{\mathrm{Vector}}^{A}=\left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{Vector}}^{B}$
$\vec{R}_{\mathrm{P}}^{A}=\left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{P}}^{B}+\vec{R}_{\mathrm{B}}^{A}$
对于固定坐标系下同一线/面，在不同坐标系 $\left\{ A \right\} ,\left\{ B \right\}$ 下进行表达，存在如下转换关系：
$\vec{R}_{\mathrm{P}}^{A}+\lambda \vec{R}_{\mathrm{Vector}}^{A}=\left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{P}}^{B}+\vec{R}_{\mathrm{B}}^{A}+\lambda \left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{Vector}}^{B}=\left[ Q_{\mathrm{B}}^{A} \right] \left( \vec{R}_{\mathrm{P}}^{B}+\lambda \vec{R}_{\mathrm{Vector}}^{B} \right) +\vec{R}_{\mathrm{B}}^{A}$
$\vec{R}_{\mathrm{P}}^{A}+\lambda _1\vec{R}_{\mathrm{Vector}_1}^{A}+\lambda _2\vec{R}_{\mathrm{Vector}_2}^{A}=\left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{P}}^{B}+\vec{R}_{\mathrm{B}}^{A}+\lambda _1\left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{Vector}_1}^{B}+\lambda _2\left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{Vector}_2}^{B}=\left[ Q_{\mathrm{B}}^{A} \right] \left( \vec{R}_{\mathrm{P}}^{B}+\lambda _1\vec{R}_{\mathrm{Vector}_1}^{B}+\lambda _2\vec{R}_{\mathrm{Vector}_2}^{B} \right) +\vec{R}_{\mathrm{B}}^{A}$ 文章来源地址https://www.toymoban.com/news/detail-819679.html