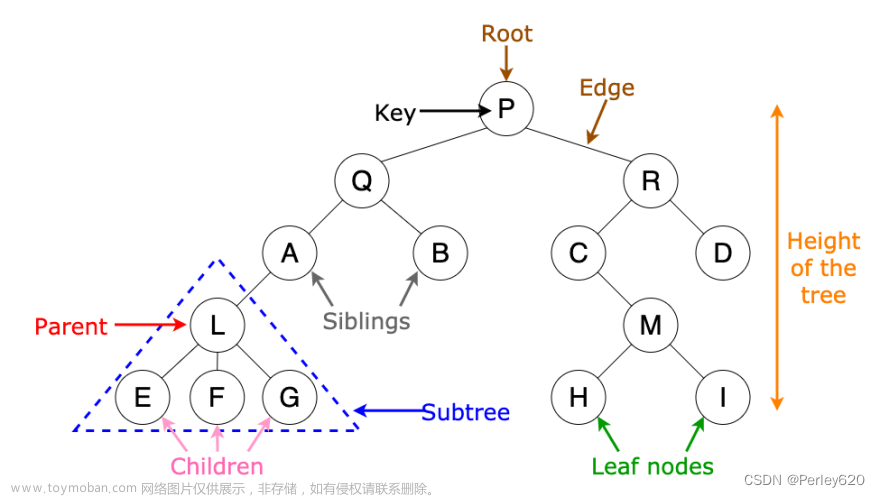
二叉排序树
- 若它的左子树不空,则左子树上所有结点的值均小于它根结点的值。
- 若它的右子树不空,则右子树上所有结点的值均大于它根结点的值。
- 它的左、右树又分为⼆叉排序树
二叉排序树也叫二叉查找树、二叉搜索树
二叉排序树的创建、插入、查找和删除
创建和插入
题目描述
给出一个数据序列,建立二叉排序树,并实现插入功能。
在建立和插入操作后,都输出二叉树的先序遍历结果i
输入
第1行输入n,表示序列包含n个数据
第2行输入n个数据,都是自然数且互不相同,数据之间用空格隔开
第3行输入m,表示要插入m个数据
输入m行,每行一个要插入的数据,都是自然数且和前面的数据不等
输出
第一行输出一开始构建的二叉排序树的先序遍历结果
从第二行起,输出m行,每行输出插入一个数据到二叉排序树后的先序遍历结果
每行输出的遍历结果中,每个数据后面都带一个空格,最后一个数据也带。
输入样例1
6
22 33 55 66 11 44
3
77
50
10
输出样例1
22 11 33 55 44 66
22 11 33 55 44 66 77
22 11 33 55 44 50 66 77
22 11 10 33 55 44 50 66 77
输入样例2
6
33 55 22 66 11 44
3
25
88
50
输出样例2
33 22 11 55 44 66
33 22 11 25 55 44 66
33 22 11 25 55 44 66 88
33 22 11 25 55 44 50 66 88
#include<bits/stdc++.h>
using namespace std;
//树节点
struct tree
{
int value=0;
tree* left=NULL;
tree* right=NULL;
};
//插入操作
tree* insert(tree* t,int a)
{
tree* root=t;
while(1)
{
if(t->value==0)
{
t->value=a;
break;
}
if(a<t->value)
{
if(!t->left) t->left=new tree;
t=t->left;
}
else
{
if(!t->right) t->right=new tree;
t=t->right;
}
}
return root;
}
//先序遍历
void prior(tree* t)
{
if(t==NULL) return ;
cout<<t->value<<" ";
prior(t->left);
prior(t->right);
}
int main()
{
int n;
cin>>n;
tree* root=new tree;
for(int i=0;i<n;i++)
{
int x;
cin>>x;
root=insert(root,x);
}
prior(root);
cout<<endl;
int m;
cin>>m;
for(int i=0;i<m;i++)
{
int x;
cin>>x;
//插入
root=insert(root,x);
prior(root);
cout<<endl;
}
return 0;
}
查找
题目描述
给出一个数据序列,建立二叉排序树,并实现查找功能
输入
第1行输入n,表示首个序列包含n个数据
第2行输入n个数据,都是自然数且互不相同,数据之间用空格隔开
第3行输入m,表示要查找m个数据
接着输入m行,每行一个要查找的数据,都是自然数
以此类推输入下一个示例
输出
第一行输出有序的数据序列,对二叉排序树进行中序遍历可以得到
从第二行起,输出查找结果,如果查找成功输出查找次数,如果查找失败输出-1
输入样例1
6
22 33 55 66 11 44
7
11
22
33
44
55
66
77
输出样例1
11 22 33 44 55 66
2
1
2
4
3
4
-1
输入样例2
6
33 22 55 11 66 44
4
88
11
44
66
输出样例2
11 22 33 44 55 66
-1
3
3
3
#include<bits/stdc++.h>
using namespace std;
//树节点
struct tree
{
int value=0;
tree* left=NULL;
tree* right=NULL;
};
//插入
tree* insert(tree* t,int a)
{
tree* root=t;
while(1)
{
if(t->value==0)
{
t->value=a;
break;
}
if(a<t->value)
{
if(!t->left) t->left=new tree;
t=t->left;
}
else
{
if(!t->right) t->right=new tree;
t=t->right;
}
}
return root;
}
//中序遍历
void middle(tree* t)
{
if(t==NULL) return ;
middle(t->left);
cout<<t->value<<" ";
middle(t->right);
}
//查找
int find(tree* t,int a,int time)
{
while(1)
{
time++;
if(t->value==0)
{
time=-1;
break;
}
if(t->value==a) break;
if(a<t->value)
{
if(!t->left) t->left=new tree;
t=t->left;
}
else
{
if(!t->right) t->right=new tree;
t=t->right;
}
}
return time;
}
int main()
{
int n;
cin>>n;
tree* root=new tree;
for(int i=0;i<n;i++)
{
int x;
cin>>x;
root=insert(root,x);
}
middle(root);
cout<<endl;
int m;
cin>>m;
for(int i=0;i<m;i++)
{
int x;
cin>>x;
cout<<find(root,x,0)<<endl;
}
return 0;
}
删除
题目描述
给出一个数据序列,建立二叉排序树,并实现删除功能
对二叉排序树进行中序遍历,可以得到有序的数据序列
输入
第一行输入t,表示有t个数据序列
第二行输入n,表示首个序列包含n个数据
第三行输入n个数据,都是自然数且互不相同,数据之间用空格隔开
第四行输入m,表示要删除m个数据
从第五行起,输入m行,每行一个要删除的数据,都是自然数
以此类推输入下一个示例
输出
第一行输出有序的数据序列,对二叉排序树进行中序遍历可以得到
从第二行起,输出删除第m个数据后的有序序列,输出m行
以此类推输出下一个示例的结果
输入样例1
1
6
22 33 55 66 11 44
3
66
22
77
输出样例1
11 22 33 44 55 66
11 22 33 44 55
11 33 44 55
11 33 44 55文章来源:https://www.toymoban.com/news/detail-819681.html
提示
当删除数据不在序列中,那么删除操作等于不执行,所以输出序列不变化文章来源地址https://www.toymoban.com/news/detail-819681.html
- 被删除的节点是叶子节点,将双亲节点中相应的指针域的值改为空
- 被删除的节点只有左子树或右子树,将要删除的节点的双亲节点相应指针域的值指向被删除节点的左子树或者右子树
- 被删除节点既有左子树又有右子树,将左子树中的最大值或者右子树中的最小值代替该节点
#include<bits/stdc++.h>
using namespace std;
//树节点
struct tree
{
int value=0;
tree* left=NULL;
tree* right=NULL;
};
//插入
tree* insert(tree* t,int a)
{
tree* root=t;
while(1)
{
if(t->value==0)
{
t->value=a;
break;
}
if(a<t->value)
{
if(!t->left) t->left=new tree;
t=t->left;
}
else
{
if(!t->right) t->right=new tree;
t=t->right;
}
}
return root;
}
//中序遍历
void middle(tree* t)
{
if(t==NULL||t->value==0) return ;
middle(t->left);
cout<<t->value<<" ";
middle(t->right);
}
//删除
void del(tree* t,int a)
{
//记录父节点
tree* p=NULL;
while(1)
{
if(t->value==0) break;
if(t->value==a)
{
//叶子结点直接删除
if(!t->left&&!t->right)
{
if(p->left==t) p->left=NULL;
else p->right=NULL;
break;
}
//只有左子树或只有右子树
if(!t->left||!t->right)
{
//左子树不空
if(t->left)
{
if(p->left==t) p->left=t->left;
else p->right=t->left;
break;
}
//右子树不空
if(t->right)
{
if(p->left==t) p->left=t->right;
else p->right=t->right;
break;
}
}
//左右子树都不空
//本做法是用左子树最大值代替该节点值
tree* now=t->left;
tree* par=t;
while(now->right)
{
par=now;
now=now->right;
}
//左子树最大值
int value=now->value;
//更新值
t->value=value;
//这里注意!!!
if(!now->left&&!now->right)
{
//直接删除左子树的根节点
if(par==t) par->left=NULL;
//删除的不是左子树的根节点
else par->right=NULL;
}
//有子节点肯定是左子节点
else par->right=now->left;
break;
}
if(a<t->value)
{
if(!t->left) t->left=new tree;
p=t;
t=t->left;
}
else
{
if(!t->right) t->right=new tree;
p=t;
t=t->right;
}
}
}
int main()
{
int t;
cin>>t;
for(int i=0;i<t;i++)
{
int n;
cin>>n;
tree* root=new tree;
for(int i=0;i<n;i++)
{
int x;
cin>>x;
root=insert(root,x);
}
middle(root);
cout<<endl;
int m;
cin>>m;
for(int i=0;i<m;i++)
{
int x;
cin>>x;
del(root,x);
middle(root);
cout<<endl;
}
}
return 0;
}
到了这里,关于二叉排序树的创建、插入、查找和删除【数据结构】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!