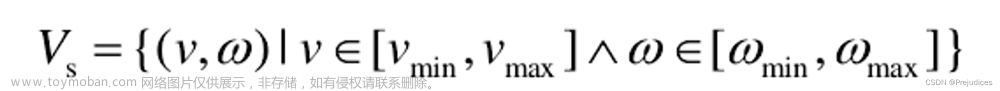两平面/三平面求交线理论推导（附C++实现）

一、两平面求交线问题描述

求解两平面的交线，两平面分别为$a_{1}x+b_{1}y+c_{1}z+d_1$和$a_{2}x+b_{2}y+c_{2}z+d_2$

1.1 数学建模

$$\{\begin{array}{r}{a}_{1}x+b_{1}y+c_{1}z+d_1=0\\ a_{2}x+b_{2}y+c_{2}z+d_2=0\end{array}(1)$$
易知平面1的法向量$n_1=(a_1,b_1,c_1{)}^T$，原点距离平面距离为$-d_1$；平面2的法向量$n_2=(a_2,b_2,c_2{)}^T$，原点距离平面距离为$-d_2$。
中学学过，知道直线的方向向量$u$和直线经过的一点$p$即可确定一条直线，我们的目标就是求取交线的$u$和$p$。

1.2 求解方向向量

显然交线同时垂直于两个平面的方向向量，即$u=n_1\times n_2$
通常为了更紧凑的表述叉积，会构造叉积矩阵
n 1 ^ = ( 0 − c 1 b 1 c 1 0 − a 1 − b 1 a 1 0 ) \hat{n_1}=\begin{pmatrix} 0& -c_1& b_1\\ c_1& 0& -a_1\\ -b_1& a_1& 0 \end{pmatrix} n1​^​= ​0c1​−b1​​−c1​0a1​​b1​−a1​0​ ​
$$\therefore u=n_1\times n_2=\widehat{n_1}\cdot n_2$$

1.3 求解直线上的一点

$p$点需要同时位于两个平面上，也就是要同时满足两个平面方程，很明显公式(1)中的因为秩明显小于未知量个数而有无穷多个解，这种情况我们只能假设其中的一个未知量已知，比如令$x=0$，求解另外两个未知量。
$$\{\begin{array}{r}{b}_{1}y+c_{1}z=-d_1\\ b_{2}y+c_{2}z=-d_2\end{array}(2)$$
解得：
$$\{\begin{array}{r}y=\frac{c_2{d}_1-c_1{d}_2}{b_2{c}_1-b_1{c}_2}\\ z=\frac{b_1{d}_2-b_2{d}_1}{b_2{c}_1-b_1{c}_2}\end{array}(3)$$

1.4 c++实现

void calIntersection(const Eigen::Vector4f& plane1_coeff, const Eigen::Vector4f& plane2_coeff, Eigen::Vector3f& line_dir, Eigen::Vector3f& line_point) {
	double a1, b1, c1, d1, a2, b2, c2, d2;
	double tempy, tempz;
	a1 = plane1_coeff[0];
	b1 = plane1_coeff[1];
	c1 = plane1_coeff[2];
	d1 = plane1_coeff[3];
	a2 = plane2_coeff[0];
	b2 = plane2_coeff[1];
	c2 = plane2_coeff[2];
	d2 = plane2_coeff[3];
	tempz = -(d1 / b1 - d2 / b2) / (c1 / b1 - c2 / b2);
	tempy = (-c1 / b1) * tempz - d1 / b1;
	line_dir << (b1 * c2 - c1 * b2), (c1* a2 - a1 * c2), (a1* b2 - b1 * a2);
	line_point << 0.0, tempy, tempz;
}

1.5 问题

很明显这个假设存在巨大的漏洞，因为很有可能交线上不存在$x=0$的点，几何意义是交线平行于$y-o-z$平面且不重合的时候。也就是对应方程(2)的系数矩阵行列式为零的时候。

因此使用这个方法时候如果为了稳定，需要进行比较复杂的条件判断，但作为有追求的人，还是想对更优雅的方案进行探索。

二、三平面求交点问题描述

上一章我们提出的方法最大的问题是，假设的交点有可能不存在。我们知道三平面可以准确的确定一个交点，那看看能不能从三平面求交点上获得灵感。

2.1 数学建模

$$\{\begin{array}{r}{a}_{1}x+b_{1}y+c_{1}z=-d_1\\ a_{2}x+b_{2}y+c_{2}z=-d_2\\ a_{3}x+b_{3}y+c_{3}z=-d_3\end{array}(4)$$

2.2 求解

任意两平面求解交线的方向向量
$$\{\begin{array}{r}u=n_1\times n_2=\widehat{n_1}\cdot n_2\\ v=n_2\times n_3=\widehat{n_2}\cdot n_3\\ w=n_3\times n_1=\widehat{n_3}\cdot n_1\end{array}$$

求解交点就是求方程(4)的解，当系数矩阵非奇异，也就是三个平面不平行的时候，方程组适定，可以求出唯一解。使用我们线性代数学习过的克莱姆法则，可以很容易求出这个线性方程组的解。

借用wiki，我们回顾一下克莱姆法则：

因此，易得三平面交点坐标为：
$$p=(\frac{det(A_1)}{det(A)},\frac{det(A_2)}{det(A)},\frac{det(A_3)}{det(A)}{)}^T$$
其中， A = ( A 1 B 1 C 1 A 2 B 2 C 2 A 3 B 3 C 3 ) A 1 = − ( D 1 B 1 C 1 D 2 B 2 C 2 D 3 B 3 C 3 ) , A 2 = − ( A 1 D 1 C 1 A 2 D 2 C 2 A 3 D 3 C 3 ) , A 3 = − ( A 1 B 1 D 1 A 2 B 2 D 2 A 3 B 3 D 3 ) A=\begin{pmatrix} A_1& B_1& C_1\\ A_2& B_2& C_2\\ A_3& B_3& C_3 \end{pmatrix}\\A_1=-\begin{pmatrix} D_1& B_1& C_1\\ D_2& B_2& C_2\\ D_3& B_3& C_3 \end{pmatrix}, A_2=-\begin{pmatrix} A_1& D_1& C_1\\ A_2& D_2& C_2\\ A_3& D_3& C_3 \end{pmatrix}, A_3=-\begin{pmatrix} A_1& B_1& D_1\\ A_2& B_2& D_2\\ A_3& B_3& D_3 \end{pmatrix} A= ​A1​A2​A3​​B1​B2​B3​​C1​C2​C3​​ ​A1​=− ​D1​D2​D3​​B1​B2​B3​​C1​C2​C3​​ ​,A2​=− ​A1​A2​A3​​D1​D2​D3​​C1​C2​C3​​ ​,A3​=− ​A1​A2​A3​​B1​B2​B3​​D1​D2​D3​​ ​

化简后可得$$p=\frac{-D_1(n_2\times n_3)-D_2(n_3\times n_1)-D_3(n_1\times n_2)}{det(A)}$$

三、启发

既然两两不平行的三个平面可以唯一的确定一个角点，那在求解两平面交线所过点时，也可以人为引入第三个平面来辅助求解，已经求出交线的方向向量为$u=(u_1,u_2,u_3{)}^T$，以$u$为法向量构建辅助平面，设原点距离辅助平面的距离为0。
$$\{\begin{array}{l}{a}_{1}x+b_{1}y+c_{1}z=-d_1\\ a_{2}x+b_{2}y+c_{2}z=-d_2\\ u_{1}x+u_{2}y+u_{3}z=0\end{array}(3)$$

void calIntersection(const Eigen::Vector4f& plane1_coeff, const Eigen::Vector4f& plane2_coeff, Eigen::Vector3f& line_dir, Eigen::Vector3f& line_point) {
	Eigen::Vector3f n1, n2, u;
	float d1, d2, d3;
	Eigen::Matrix3f A;
	n1 = plane1_coeff.block<3, 1>(0, 0);
	n2 = plane2_coeff.block<3, 1>(0, 0);
	u = n1.cross(n2);
	d1 = plane1_coeff[3];
	d2 = plane2_coeff[3];
	d3 = 0;
	A << n1, n2, u;
	line_dir = u;
	line_point = (-d1 * n2.cross(u) - d2 * u.cross(n1) - d3 * n1.cross(n2)) / A.determinant();
}

这样就不需要担心最开始提到的问题了文章来源地址https://www.toymoban.com/news/detail-820240.html

到了这里，关于两平面/三平面求交线理论推导（附C++实现）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！