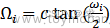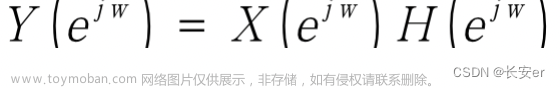FIR数字滤波器设计-Toy模板网

这篇具有很好参考价值的文章主要介绍了FIR数字滤波器设计。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目标
用Kaiser窗设计一个FIR数字带阻滤波器，对模拟信号 $x_a(t) = cos (2\pi f_at) + cos (2\pi f_bt) + cos (2\pi f_ct)$ ，
$f_a = 6500 Hz，f_b = 7000 Hz，f_c = 9000 Hz$ 滤波，要求滤去7000Hz 的频率成分。
参数
系统采样频率为 $f_s$ = 32000 Hz，采样点数 N=4096，滤波器的通带衰减 $R_p$ = 0.25 dB，阻带衰减 $\alpha$ = 50 dB，过渡带宽可以用模拟频率（例如200Hz）也可以用数字频率指定。

【 1. 具体实现】

旁瓣衰减为 α dB 且表示 FIR 滤波器的凯塞窗，此时的形状因子为：
$\left.\beta=\left\{\begin{array}{ll}0.1102(\alpha-8.7),&\alpha>50\\ 0.5842(\alpha-21)^{0.4}+0.07886(\alpha-21),&50\geq\alpha\geq21\\ 0,&\alpha<21\end{array}\right.\right.$
阶数
$n=\frac{\alpha _s-8}{2.285\times \Delta w}$
MATLAB实现代码

clc;
clear;
close all;

%% 【1. 设定参数】
%%% 采样参数
fs = 32000; %采样频率
Ts = 1/fs;  %采样周期
N  = 4096;  %采样点数
t  = 0:Ts:(N-1)*Ts; %时间刻度
%%% 原信号参数
fa = 6500;
fb = 7000;
fc = 9000;
xa = cos(2*pi*fa*t)+cos(2*pi*fb*t)+cos(2*pi*fc*t);

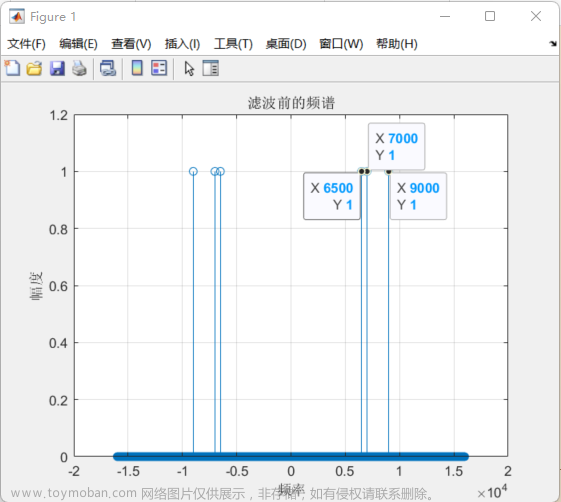
%% 【3. 滤波前：fft频谱】
%%% FFT
M = 4096; %FFT的运算点数
Xa = fft(xa,M);   %FFT输出值
Xa = [Xa(1)/M,Xa(2:M)*2/M]; %幅度轴
Xa_fftshift = fftshift(Xa); %频域搬移
k = -M/2:M/2-1;  %频率点索引
f = fs*k/M;      %频率轴
%%% 画图
figure;
stem(f,abs(Xa_fftshift));
xlabel('频率');
ylabel('幅度');
title('滤波前的频谱');
grid;

%% 【4. 滤波器设计：加Kasier窗的FIR滤波器】
%%% 滤波器参数
Rp = 0.25; %通带衰减，单位dB，(未用到)
alpha  = 50;   %阻带衰减，单位dB
fstart = 6900; % 阻带起始频率
fstop  = 7100; % 阻带终止频率
beta = 0.1102*(alpha-8.7); % 形状因子beta
Wn   = [2*fstart/fs  2*fstop/fs];% 阻带带宽，两个截止角频率(归一化)，截至范围：6900hz-7100hz
Wfs  = 2*pi*(fstop-fstart)/2/fs; % 归一化过渡带宽
n    = (alpha-8)/(2.285*Wfs); %阶数
n    = ceil(n);      % 向上取整
n    = n + mod(n,2); % 取偶
%%% 生成凯塞窗
Windows      = kaiser(n+1,beta); %凯撒窗
KasierFilter = fir1(n,Wn, 'stop', Windows);
%%% 画图
[H, W] = freqz(KasierFilter,1,4096,fs); %返回凯塞窗滤波器的频率响应H,角频率W
figure;
freqzplot(H,W); %频率响应
title("滤波器的频率响应");
ylabel('dB');

%% 【5. 信号输入滤波器：最终效果】
After_filter = filter(KasierFilter,1,xa);%把信号输入滤波器
Xa1 = fft(After_filter,M);   %FFT输出值
Xa1 = [Xa1(1)/M,Xa1(2:M)*2/M]; %幅度轴
Xa1_fftshift = fftshift(Xa1); %频域搬移
k = -M/2:M/2-1;  %频率点索引
f = fs*k/M;      %频率轴
%%% 画图
figure;
stem(f,abs(Xa1_fftshift));
xlabel('频率');
ylabel('幅度');
title('滤波后的频谱');
grid;