目录
一. 求解Ax=b
二. 上三角矩阵分解
三. 下三角矩阵分解
四. 矩阵的三角分解
举例1:矩阵三角分解
举例2:三角分解的限制
举例3:主元和乘法因子均为1
举例4:U为单位阵
小结
一. 求解Ax=b
我们知道高斯消元法可以对应矩阵的基础变换。先来看我们比较熟悉的Ax=b模型,如下:
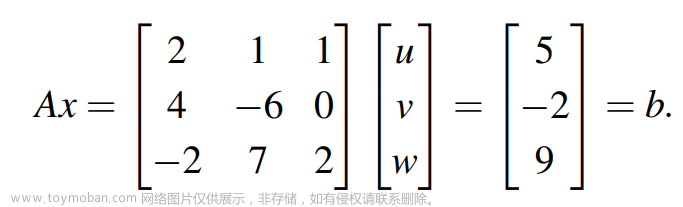
解这个方程很简单,只需要三步高斯消元步骤,分别乘以2,-1,-1.
第一步:第二行减去第一行乘以2倍;
第二步:第三行减去第一行乘以-1;
第三步:第三行减去第二行乘以-1;
以上方程中的系数矩阵A会变成新的系数矩阵(coefficient matrix)U,由此得到等效的方程组:
Ux=c
很明显,此时的U为上三角矩阵,也就是对角线往下的位置均为0,如下:

把矩阵A变成矩阵U的过程记录下来,同样的步骤运用在b上就可以变成等式右边的c,我们把这个过程可称之为前向消元过程(forward elimination),其关键的步骤有三步:
- 从矩阵A和向量b开始;
- 按顺序进行以上三步;
- 形成新的矩阵U与向量c
接着方程Ux=c,就可以被后向带入法(back substitution)解决。
二. 上三角矩阵分解
在刚才的解方程过程中,我们经历了如何把矩阵A变成上三角矩阵U。总共分成三步,可以把每一步抽象成一种矩阵变换,第一步叫矩阵E,第二步叫矩阵F,第三步叫矩阵G,这些矩阵都可以被称之为初等矩阵(elementary matrix)。
那么这些初等矩阵长啥样?
用第i行减去第j行的l倍,那么相等于在矩阵的(i,j)位置,放上-l.对角线上均为1,其他位置均为0,这就是初等矩阵的规律。
需要注意的是,矩阵乘法执行的是行操作,由此可得:
GFEA=U
注意A首先与E相乘,接着是F,最后是矩阵G。
此时可思考一个问题:如果把GFE乘在一起,是不是可以将以上变换合并为一个矩阵,该矩阵可直接把A变成U,同理可以把b变成c。实际上此矩阵为下三角矩阵,省去0,该矩阵即为:

三. 下三角矩阵分解
在以上我们学习了如何把矩阵A变成矩阵U,那么反过来,如何把矩阵U变成A呢?或者换句话说,高斯消元的逆步骤如何理解呢?
首先来看第一步的操作。高斯消元的第一步是第二行减去第一行的两倍,那么逆步骤就是第二行加上第一行的两倍,也就是减去第一行的负两倍,所以(2,1)位置为2,换句话说减法的逆运算即为加法,由此可得:

我们发现加法和减法相乘的结果即为单位阵,这样就可以抵消掉其操作,其实就是求其逆矩阵。
我们来总结下规律。
如果初等矩阵第(i,j)位置为-l,那么其逆矩阵则在相同的位置变成=l,由此可得:
利用同样的方法,我们可以把E,F,G的逆矩阵全部求出来,记为:
接下来我们学习如何用一个矩阵实现从U变成A。原高斯消元的最后一步是第三步就可以实现从A到U,那么在求逆时相关的矩阵G则是第一步求逆,也就是求逆是相反步骤,如下:
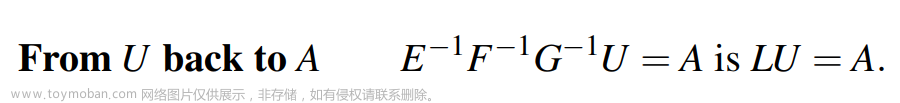
由此我们便实现了A=LU的过程。
以上L为下三角矩阵(lower triangular),该下三角矩阵的运算非常直接,如下:
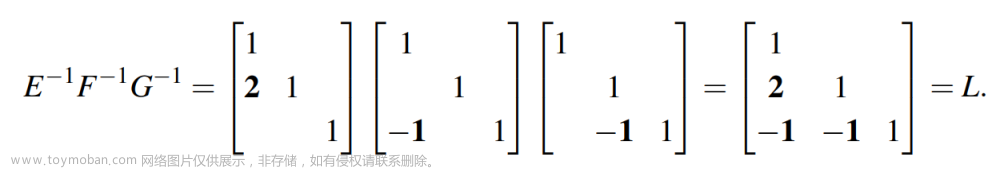
观察可以发现该矩阵对角线往下的元素则为乘法因子2和-1,-1
以上运算中的乘法因子即为:
该因子代表第i行减去第j行的主元,接着在第i行对应的位置出现0,则为实际高斯消元法的步骤。
四. 矩阵的三角分解
三角分解,又称之为Triangular factorization,在网络安全等领域非常多。
在不改变行的情况下,矩阵三角分解如:
A=LU
其中L为下三角矩阵,且对角线处的元素为1。从高斯消元的步骤中获取乘法因子lij,这些元素的值都位于对角线的下面。
U为上三角矩阵,在正向消元步骤结束后可获取,矩阵U对角线处的元素则可称之为主元(pivots)。
举例1:矩阵三角分解
给出矩阵A如下:

将矩阵分解为A=LU,其中U为上三角矩阵如下:
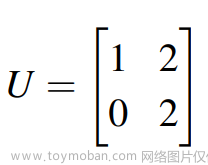
L为下三角矩阵且对角线处的元素值为1,如下:
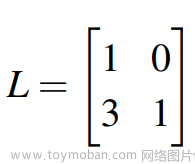
举例2:三角分解的限制
并不是所有的方阵都可以分解为A=LU,比如举个例子:

实际上需要做一个行交换则可以分解。
举例3:主元和乘法因子均为1
给定如下三阶方阵:

对其进行三角分解A=LU可得:

可以发现此时矩阵的乘法因子和主元均为1,也就是行变换都是直接相减。换句话说从U变成A只有行直接相加的过程。
举例4:U为单位阵
看一个特殊的矩阵A,其刚好为下三角矩阵且对角线处的值为1,如下:

对该矩阵进行高斯消元则非常简单,可分成三步:
第一步:矩阵E:第二行减去第一行的倍
第二步:矩阵F:第三行减去第一行的倍
第三步:矩阵G:第三行减去第二行的倍
此时可以发现U=I
同理对矩阵E,F,G求逆便可以还原出矩阵A,如下:
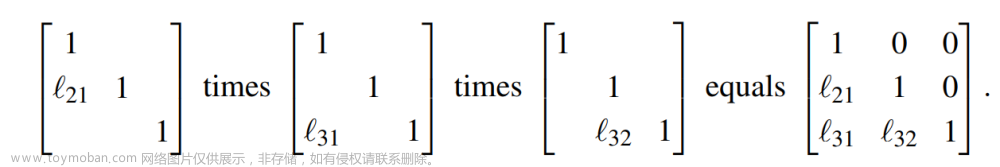
注意以上运算满足矩阵的结合率。
小结
我们知道基于代数余子式的行列式计算方法,该方法计算量大,难以实现大型矩阵的行列式计算。所以,应该想办法将矩阵的某些元素变换为零,又不影响行列式的求值。比较好的方法是进行初等行变换的运算,可以将矩阵的一些元素有目的地变换成零。
在线性代数领域,有三种初等行变换方法,然后将其应用于矩阵求矩阵初等行变换的基础是三种常用的矩阵初等行变换方法。
下面的三种变换称为矩阵的初等行变换:
(1)将矩阵的某一行元素同时乘以常数k,其他元素不变;
(2)将矩阵的某一行所有元素乘以常数k 并加到另一行上;文章来源:https://www.toymoban.com/news/detail-821070.html
(3)将矩阵的任意两行互换,其他行的元素不变。文章来源地址https://www.toymoban.com/news/detail-821070.html
到了这里,关于详解矩阵的三角分解A=LU的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!