旅行售货商问题
题目描述
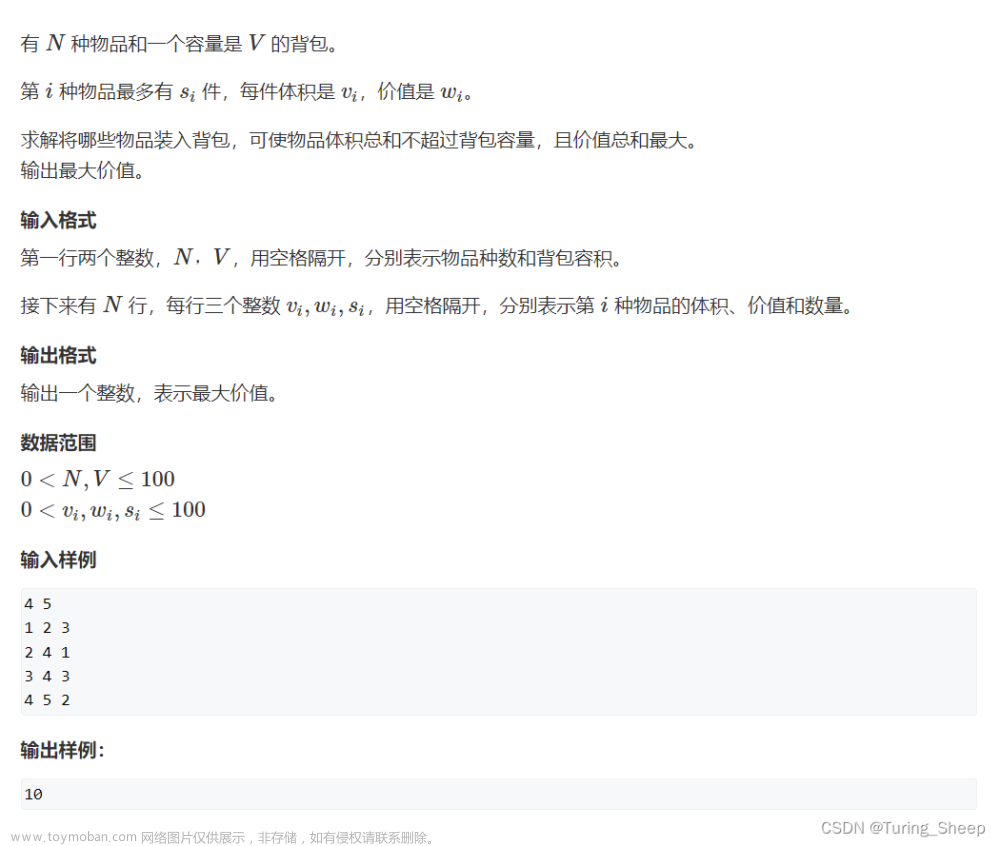
一个国家有 n 个城市,每两个城市之间都开设有航班,从城市 i 到城市 j 的航班价格为 cost[i, j] ,而且往、返航班的价格相同。
售货商要从一个城市出发,途径每个城市 1 次(且每个城市只能经过 1 次),最终返回出发地,而且他的交通工具只有航班,请求出他旅行的最小开销。
关于输入
输入的第 1 行是一个正整数 n (3 <= n <= 15)
然后有 n 行,每行有 n 个正整数,构成一个 n * n 的矩阵,矩阵的第 i 行第 j 列为城市 i 到城市 j 的航班价格。
关于输出
输出数据为一个正整数 m,表示旅行售货商的最小开销
例子输入
4 0 4 1 3 4 0 2 1 1 2 0 5 3 1 5 0
例子输出
7
解题分析
对于这个问题,如果我们直接用递归回溯的办法给n个城市进行全排列(类似于八皇后问题的方法),然后再计算每种排列下我们需要的开销是多少,可以解决当所给数组n比较小的时候,而这种算法的时间复杂度是n!,当n增大时,算法所需要的时间会急剧增大,所以很容易就timeout了。我们需要想出另外的方法去解决本问题。
注意到,在题干描述之下,问题是对称的,我们任意选取一个城市作为初始城市,然后去求这个的问题的最小开销,结果是一样的。例如,如果2 ---->0------>1----->3------>2是最小开销(最短路程),那么,如果我们如果选0作为出发点,0------>1----->3-------2----->0,显然两种情况答案一样,故,我们不妨令城市0为我们的商人的出发点。
那,我们如何定义动态规划的dp数组呢?我们又如何存储哪些城市已经访问过了,那些没有?这里,我们引入一个重要的方法,二进制状态压缩。
我们用一个二进制数去保存城市访问的状态,例如,如果我们有4个城市,那么,初始的状态就是0000,如果我们去过了0城市,则状态为0001,如果我们去过了0城市和3城市,那状态为1001,这样,我们巧妙地存储了去过的城市的状态,结合位于算与(&)和或(|),我们可以进一步的判断并更新动态规划的方程。
此程序使用深度优先搜索(DFS)和动态归划(DP)的方法解决旅行售货商问题(又称旅行商问题TSP,traveling salesman problem)。
程序的整体思路是:
1. 从一个城市出发(设为0,且在其他城市中只能访问每个城市一次),通过遍历所有可能的旅行线路,找到花费最小的深度优先搜索线路。
2. 然后在所有可能的旅行线路中选择花费最小的线路,最终找到总的最小花费线路。
下面逐个详解程序中的关键部分。
深度优先搜索函数:`dfs(int mark, int pos)`
在这个函数中,参数`mark`为访问过的城市的标记,`pos`为当前所在城市。
- 若`mark`等于`(1<<n)-1`,表示所有城市都已访问过,返回`cost[pos][0]`(即从当前城市返回出发城市的花费)。
- 若访问过的城市路径`dp[mark][pos]`已被计算过(不等于-1),直接返回已存储的最小花费。
- 若城市`i`未被访问过(即`mark & (1<<i)`结果为0),计算从当前城市到城市`i`的花费+从城市`i`开始,访问剩余未访问城市的最小花费,其结果和当前最小花费比较取小值,遍历所有城市后得到`ans`,即从当前城市开始最小花费。
- 将计算得到的`ans`存入`dp[mark][pos]`并返回。
主函数`main(void)`部分则是将旅行售货商问题的初始条件接收(城市数,各城市间的花费),并初始化动态规划矩阵`dp`,然后使用深度优先搜索找到最低花费,最后输出最低花费。
这个程序主要通过深度优先搜索去遍历每一种可能的线路,并通过动态规划记忆已经搜索过的线路,以此剪枝,降低复杂度。
在这个问题中,动态规划数组dp用于存储已经计算过的结果,以减少重复计算。动态规划在旅行售货商问题中的任务是记忆化搜索的工具。
每一行的索引mark用于表示已经访问过的城市。具体来说,将mark按二进制翻译后,如果某一位为1,表示对应索引的城市已经被访问过;如果为0,表示还未访问过。
每一列的索引pos表示当前所在的城市。
dp[mark][pos]存放已经访问过标记为mark的城市,并且当前所在城市为pos的情况下,回到出发城市的最小开销。这里的最小开销包括了从当前城市直接返回到出发城市的费用和未来会访问到的其他所有城市的费用。
例如,令 n = 4,如果我们在第二个城市,已经访问过第二个和第三个城市(我们假设城市的索引从0开始),那么mark将为0110,转换为十进制则为 6。这时dp[6][1]就表示从第二个城市出发,访问除出发城市和已访问过的城市(这里是城市1和城市2)以外的所有城市(这里是城市0和城市3),并最终回到出发城市的最小花费。
在运行的过程中,如果dp[mark][pos] 等于-1,表示这个值还没有计算过,需要通过深度优先搜索计算得出。如果dp[mark][pos]不等于-1,表示这个值已经计算过,无需重新计算,直接用这个值即可,这是记忆化搜索的一种策略。
这个程序主要使用了两种位运算:位与(&)和位或(|),来记录和标记已经访问过的城市。这是一种常用于处理状态压缩动态规划的手段。
位与运算(&):
位运算中的与运算主要用来判断一个数的某一位是否为1。在程序中,mark & (1<<i)主要用来判断第i个城市是否被访问过。
给一个简单例子,假设n = 4,已经访问过的城市是城市1和城市2,那么mark就是0110。我们想要知道城市3(从0开始计数)是否被访问过,就可以用mark & (1<<3)进行计算:
0110 //mark
1000 //(1<<3)
----
0000 //结果,第3位为0,表示没有访问过
因此我们知道城市3没有被访问过。按照这种方法,我们就可以循环检测是否visited每个城市。
位或运算(|):
位运算的或运算主要用来将一个数的某一位设置为1。在程序中,(mark | (1<<i))用来标记城市i已经被访问过。
给一个简单例子,现在要标记城市3已经被访问,那么就可以 (mark | (1<<3))进行计算,结果用来更新mark。
这个问题中,因为售货商需要遍历每一个城市并返回起点,所以我们需要对每个城市进行状态的记录,记录哪些城市已经遍历过,哪些城市还未遍历,这个就是我们的状态。状态的转移则是从已经访问某些城市的情况下,转移到访问了更多城市的情况。
定义动态规划的状态dp[mark][pos],表示已经访问过标记为mark的城市,并且当前所在城市为pos的情况下,回到出发城市(城市0)的最小花费。
那么,我们的动态规划转移方程就可以设计为如下形式:
dp[mark][pos] = min(dp[mark][pos], cost[pos][i] + dp[mark | (1<<i)][i]),当i不在mark中。
解释一下这个方程:
-
对于状态
dp[mark][pos],表示已经访问过mark表示的城市,并且当前在pos城市的情况下,返回起始城市的最小费用。 -
为了找到这个最小费用,我们需要遍历所有未访问过的城市
i(i不在mark中)。考虑从当前城市pos走到未访问过的城市i,然后的费用应当为cost[pos][i] + dp[mark | (1<<i)][i]。在这个式子中,cost[pos][i]表示从城市pos到城市i的费用,dp[mark | (1<<i)][i]表示访问了城市i以及当前mark所表示的所有城市,并且最后到达城市i后,返回起始城市的最小费用。 -
在遍历了所有的可能城市
i后,就可以找到dp[mark][pos]的最小值,也就是说在已经访问过mark表示的城市,并且目前在pos城市的情况下,返回起始城市的最小费用。
这样就得到了这个问题的动态规划方程,只需要使用深度优先搜索来遍历所有的可能状态,并用记忆化搜索来记录中间结果,就可以找到问题的最优解。文章来源:https://www.toymoban.com/news/detail-821123.html
代码实现
#include <stdio.h>
#define min(x,y) x<y?x:y
#define MAXN 16
int INF=1e9;
int n;
int dp[1<<MAXN][MAXN],cost[MAXN][MAXN];
int dfs(int mark,int pos){
if(mark==(1<<n)-1){
return cost[pos][0];
}
if(dp[mark][pos]!=-1){
return dp[mark][pos];
}
int ans=INF;
for(int i=0;i<n;i++){
if((mark & (1<<i))==0){
ans=min(ans,cost[pos][i]+dfs((mark | (1<<i)),i));
}
}
return dp[mark][pos]=ans;
}
int main(void) {
scanf("%d",&n);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
scanf(" %d",&cost[i][j]);
}
for(int i=0;i<(1<<n);i++)
for(int j=0;j<n;j++){
dp[i][j]=-1;
}
int result=dfs(1,0);
printf("%d\n",result);
return 0;
}
(c++版本)文章来源地址https://www.toymoban.com/news/detail-821123.html
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 16;
const int INF = 1e9;
int n;
int dp[1<<MAXN][MAXN], cost[MAXN][MAXN];
int tsp(int mask, int pos) {
if(mask==(1<<n)-1)
return cost[pos][0];
if(dp[mask][pos]!=-1)
return dp[mask][pos];
int ans = INF;
for(int i=0; i<n; i++) {
if((mask&(1<<i))==0)
ans = min(ans, cost[pos][i] + tsp(mask|(1<<i), i));
}
return dp[mask][pos] = ans;
}
int main() {
cin>>n;
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
cin>>cost[i][j];
}
}
for(int i=0; i<(1<<n); i++) {
for(int j=0; j<n; j++) {
dp[i][j] = -1;
}
}
cout<<tsp(1, 0)<<endl; // start from city 0
return 0;
}
到了这里,关于[动态规划,二进制状态压缩] 旅行商问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!