动态规划-背包问题详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划-背包问题详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

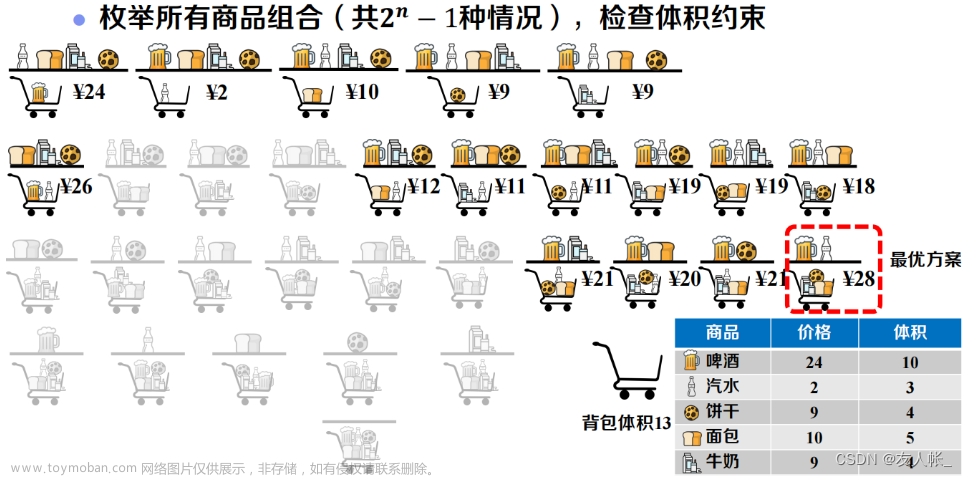
一、动态规划问题说明

1.题目问题

首先给出背包的容量，接着：

01背包问题：给出每个物品的体积和质量，每个物品最多只能使用一次
完全背包问题：给出每个物品的体积和质量，每个物品可以无限次使用
多重背包问题：给出每个物品的体积、质量和数量，每个物品使用量必须在每个物品给定的数量之类
分组背包问题：给出每个物品的体积、质量和它们的分组，每个组中最多只能取一件物品

在背包的限制之内，做出抉择，选择物品填充背包，使得最终背包的质量最大。

2.Dp解题思路

Dp由于变化较多，没有固定模板，可以从两个方面入手分析，即：状态表示和状态计算，我们把状态设为f[i][j]

状态表示f[i][j]:它表示在前i种物品种选取，使得容量不超过j，满足该情况的所有情况集合，在集合中选取最优解，该最优解的质量即为f[i][j]的值
状态计算：即如何计算f[i][j]，每种情况有所不同，且可以优化，优化方式也有所不同，在下面实例分析中进行详细讲解

二、01背包问题

1.问题描述

有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。

第 i件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

输出样例

2.朴素算法

我们可以把f[i][j]的状态计算下分，分为对两种情况的取最大值：不包括第i种物品和包括第i种物品
不包括第i种物品：f[i-1][j]
包括第i种物品：f[i-1][j-v[i]]+w[i]，即已经含有了第i种物品

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010; //物品的最大数量 

int n,m; //n是物品数量，m是背包的容量
int v[N], w[N]; //v[i]是第i件物品的体积，w[i]是第i件物品的质量
int f[N][N]; //状态表示,全局变量初始化为0 

int main()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ ) cin >> v[i] >> w[i];
	
	for(int i = 1;i <= n;i ++ )
	    for(int j = 0;j <= m;j ++ )
	    {
	    	f[i][j] = f[i - 1][j];
	    	//只有在给定的j容量大于第i个物品的体积时，才可以放第i个物品，不然程序会错误 
	    	if(j >= v[i]) f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
		}
		
	cout << f[n][m] << endl;
	
	return 0;
}

3.优化算法

我们可以把二维f[i][j]化为一维f[j]
状态计算则变为：f[j]=max(f[j],f[j-v[i]]+w[i])
出现问题：如果第二个循环依旧从前往后，则计算f[j]=max(f[j],f[j-v[i]]+w[i])时，已经在第i层中遍历过f[j-v[i]]+w[i]，即此时的f[j-v[i]]+w[i]用二维表示为f[i-1][j-v[i]]+w[i]，而非f[i][j-v[i]]+w[i]，所以第二个循环要从后往前遍历
第二个循环可以再简化：j的最小值遍历到v[i]，由于所有f[0~n][j]都存在f[j]中，所以不用遍历小于等于v[i]的部分

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010; //物品的最大数量 

int n,m; //n是物品数量，m是背包的容量
int v[N], w[N]; //v[i]是第i件物品的体积，w[i]是第i件物品的质量
int f[N]; //状态表示,全局变量初始化为0 

int main()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ ) cin >> v[i] >> w[i];
	
	for(int i = 1;i <= n;i ++ )
	    for(int j = m;j >= v[i];j -- )
	    	f[j] = max(f[j],f[j - v[i]] + w[i]);
		
	cout << f[m] << endl;
	
	return 0;
}

三、完全背包问题

1.问题描述

有 N种物品和一个容量是 V的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

输出样例

2.朴素算法

状态计算：我们把f[i][j]分为多种情况取最大值，不取第i个物品，取1个第i个物品，取两个，取三个…，但是满足前提条件是所取的第i物品总质量不大于给定的容量

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010; //物品的最大数量 

int n,m; //n是物品数量，m是背包的容量
int v[N], w[N]; //v[i]是第i件物品的体积，w[i]是第i件物品的质量
int f[N][N]; //状态表示,全局变量初始化为0 

int main()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ ) cin >> v[i] >> w[i];
	
	for(int i = 1;i <= n;i ++ )
	    for(int j = 0;j <= m;j ++ )
	    	for(int k = 0;k * v[i] <= j;k ++ )
	    	f[i][j] = max(f[i][j],f[i-1][j - k * v[i]] + k * w[i]);
	    	//由于k从0开始，所以已经包含了f[i-1][j]，不需要单独列出 
		
	cout << f[n][m] << endl;
	
	return 0;
}

3.优化算法

f[i][j]=max(f[i-1][j],f[i-1][j-v]+w,f[i-1][j-2v]+2w,f[i-1][j-3v]+3w,…)
f[i][j-v]=max(f[i-1][j-v],f[i-1][j-2v]+w,f[i-1][j-3v]+2w,…)
综上：f[i][j]=max(f[i-1][j],f[i][j-v]+w)
继续优化为一维，不过不用倒置，因为都在第i层

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010; //物品的最大数量 

int n,m; //n是物品数量，m是背包的容量
int v[N], w[N]; //v[i]是第i件物品的体积，w[i]是第i件物品的质量
int f[N]; //状态表示,全局变量初始化为0 

int main()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ ) cin >> v[i] >> w[i];
	
	for(int i = 1;i <= n;i ++ )
	    for(int j = v[i];j <= m;j ++ )
	    	f[j] = max(f[j],f[j - v[i]] + w[i]);
		
	cout << f[m] << endl;
	
	return 0;
}

四、多重背包问题

1.问题描述

有 N 种物品和一个容量是 V的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N≤1000
0<V≤2000
0<vi,wi,si≤2000

输入样例

输出样例

2.朴素算法

在完全背包问题的朴素算法基础上进行
增加一个判断条件：第三个循环多一个k<=s[i]

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010; //物品的最大数量 

int n,m; //n是物品数量，m是背包的容量
int v[N], w[N],s[N]; //v[i]是第i件物品的体积，w[i]是第i件物品的质量，s[i]是第i件物品有多少件
int f[N][N]; //状态表示,全局变量初始化为0 

int main()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ ) cin >> v[i] >> w[i] >> s[i];
	
	for(int i = 1;i <= n;i ++ )
	    for(int j = 0;j <= m;j ++ )
	    	for(int k = 0;k * v[i] <= j && k <= s[i];k ++ )
	    	f[i][j] = max(f[i][j],f[i-1][j - k * v[i]] + k * w[i]);
	    	//由于k从0开始，所以已经包含了f[i-1][j]，不需要单独列出 
		
	cout << f[n][m] << endl;
	
	return 0;
}

3.优化算法

利用二进制思想，进行拆包简化
2⁰，2¹，2²，2³…2^k：可以表示出从0到2^k-1其中的所有数
2⁰，2¹，2²，2³…2^k，C：可以表示出从0到2^k+C-1其中的所有数
接着做一遍01背包问题
注意：该题相当于把每个物品拆包为logw个物品，所以开N空间时，开为N*logw_max

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 2500; //物品的最大数量,N+logw 

int n,m; //n是物品数量，m是背包的容量
int v[N], w[N]; //v[i]是第i件物品的体积，w[i]是第i件物品的质量
int f[N]; //状态表示,全局变量初始化为0 

int main()
{
	cin >> n >> m;
	
	int cnt=0;
	
	for(int i = 1;i <= n;i ++ )
	{
		int a,b,s;
		cin >> a >> b >> s;
		int k = 1;
		while(k <= s)
		{
			cnt ++ ;
			v[cnt] = a * k;
			w[cnt] = b * k;
			s -= k;
			k *= 2;
		}
		if(s>0) //防止s刚好用完
		{
			cnt ++;
			v[cnt] = a * s;
			w[cnt] = b * s;
		}
	}
	
	n = cnt; //此时物品相当于有cnt个 
		
	for(int i = 1;i <= n;i ++ )
	    for(int j = m;j >= v[i];j -- )
	    	f[j] = max(f[j],f[j - v[i]] + w[i]);
		
	cout << f[m] << endl;
	
	return 0;
}

五、分组背包问题

1.问题描述

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。

接下来有 N 组数据：

每组数据第一行有一个整数 Si，表示第 i 个物品组的物品数量；
每组数据接下来有 Si 行，每行有两个整数 vij,wij，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤100
0<Si≤100
0<vij,wij≤100

输入样例

输出样例

2.优化算法

相当于在01背包问题上多了一个分组
分组用一个循环实现，增加第三个循环，遍历每种选择一组中任何一种的情况，取最优解

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 110; //物品的最大数量 

int n,m; //n是物品数量，m是背包的容量
int v[N][N], w[N][N],s[N]; //v[i][j]是第i组第j件物品的体积，w[i][j]是第i组第j件物品的质量,s[i]是第i组有多少个物品 
int f[N]; //状态表示,全局变量初始化为0 

int main()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ )
	{
		cin >> s[i]; //s[i]是第i组有多少个物品 
		for(int j = 0;j < s[i];j ++ )
			cin >> v[i][j] >> w[i][j];
	}
	
	for(int i = 1;i <= n;i ++ )
	    for(int j = m;j >= 0;j -- )
	    	for(int k = 0;k < s[i] && v[i][k] <= j;k ++ )
	    		f[j] = max(f[j],f[j - v[i][k]] + w[i][k]);
		
	cout << f[m] << endl;
	
	return 0;
}

六、总结

从上例我们可以看到，01背包问题、多重背包问题、分组背包问题其实十分相似，多重背包优化是进行二进制操作拆包后的01背包优化，分组背包优化是多了一个循环的01背包优化，第二个循环都需要倒置。而完全背包问题相较于01背包问题优化，唯一的区别在于第二个循环是否倒置。文章来源地址https://www.toymoban.com/news/detail-821878.html

到了这里，关于动态规划-背包问题详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！