Python多项式回归sklearn-Toy模板网

这篇具有很好参考价值的文章主要介绍了Python多项式回归sklearn。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、理论介绍

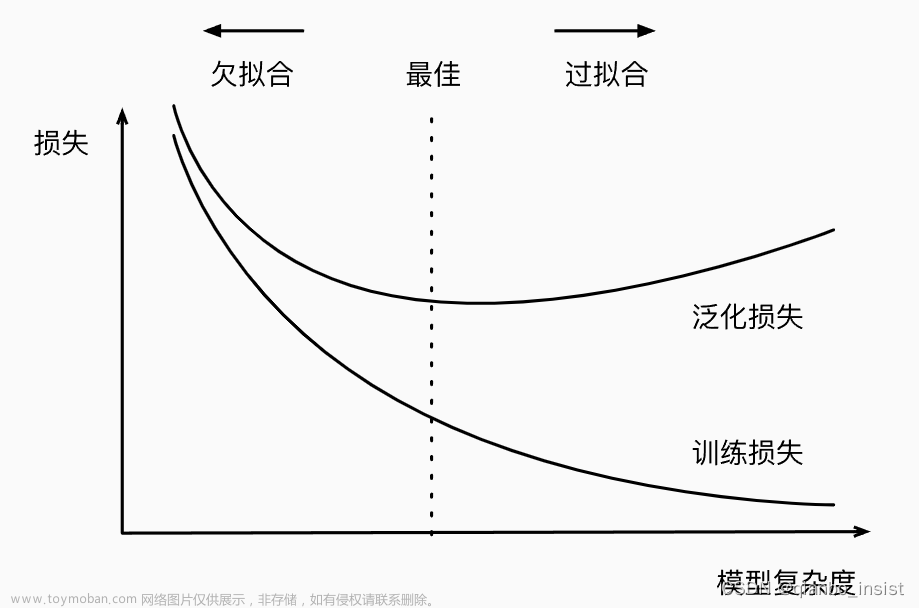
多项式回归是一种回归分析的方法，它通过使用多项式函数来拟合数据。与简单线性回归不同，多项式回归可以更灵活地适应数据的曲线特征，因为它可以包含多个特征的高次项。

多项式回归的一般形式为：
Python多项式回归sklearn,机器学习,python,回归,sklearn,算法

在实际应用中，可以通过调整多项式的次数来适应不同的数据特征。然而，过高的多项式次数可能导致过拟合，对新数据的泛化能力较差。

多项式回归可以通过最小化损失函数来找到最优的回归系数。一种常见的方法是使用最小二乘法。

在Python中，可以使用各种库（如NumPy、SciPy和scikit-learn）来实现多项式回归。例如，scikit-learn提供了PolynomialFeatures和LinearRegression等类来实现多项式回归。

Python多项式回归sklearn,机器学习,python,回归,sklearn,算法

二、案例分析

# -*- coding: utf-8 -*-
"""
Created on 2024.1.22

@author: rubyw
"""

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 载入数据
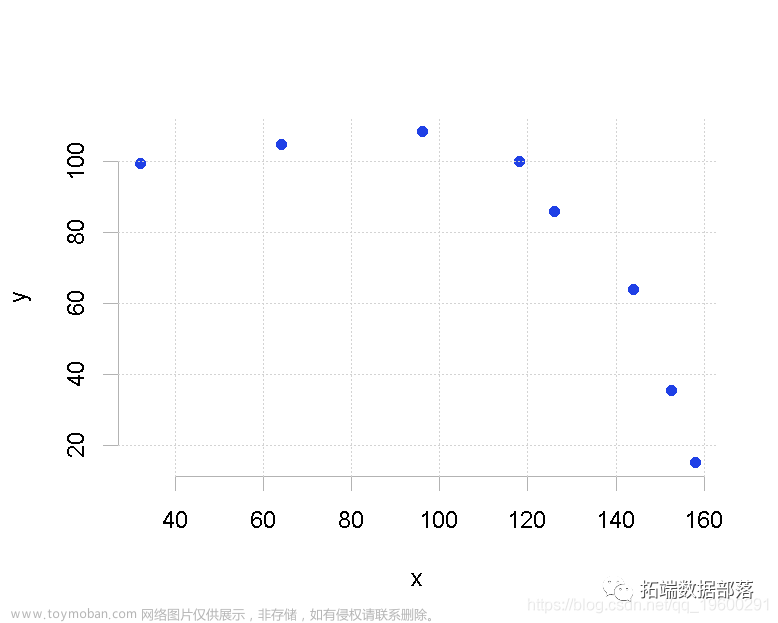
data = np.genfromtxt('job.csv', delimiter=",")
x_data = data[1:,1]
y_data = data[1:,2]
plt.scatter(x_data,y_data)
plt.show()

x_data = data[1:,1,np.newaxis]
y_data = data[1:,2,np.newaxis]
# 创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)

# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()

# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg  = PolynomialFeatures(degree=1)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)
# 定义回归模型
lin_reg = LinearRegression()
# 训练模型
lin_reg.fit(x_poly, y_data)

# 输出回归系数
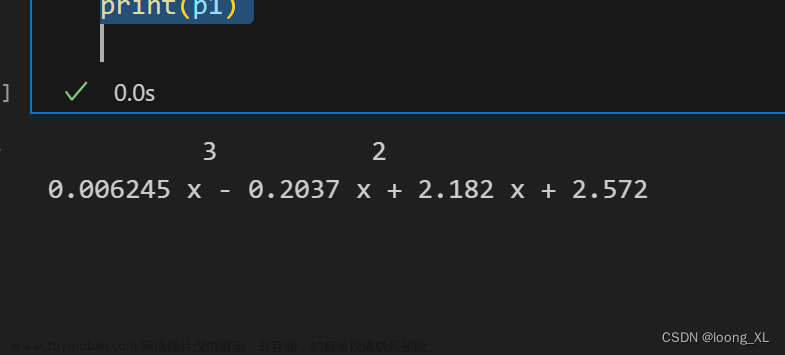
print("回归系数 (a_n, a_{n-1}, ..., a_1, a_0):", lin_reg.coef_[0])


# 画图
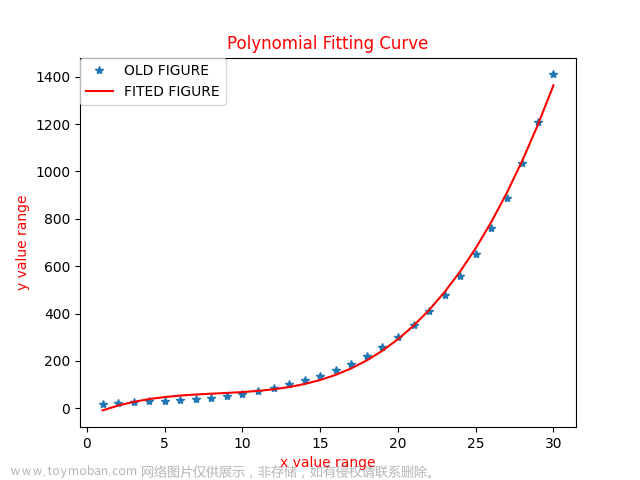
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, lin_reg.predict(poly_reg.fit_transform(x_data)), c='r')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()