目录
一、关联规则挖掘
二、Apriori-关联规则算法
三、Apriori算法分解—Python大白话式实现
步骤1: 外部库调用❀
步骤2: 数据导入❀
步骤3: 数据处理❀
步骤4:输出所有Goodlist❀
步骤5:项集重组❀
步骤6:支持度扫描与输出 ❀
步骤7:根据最小支持度阈值进行减枝叶❀
步骤8:对每一个频繁项集进行子集拆分计算confi和rule挖掘❀
步骤9:Find_rule❀
四、Apriori代码——全部呈上~
五、总结
一、关联规则挖掘
1. 定义:参考百度百科即可:
“假设是项的集合。给定一个交易数据库D,其中每个事务(Transaction)t是I的非空子集,即,每一个交易都与一个唯一的标识符TID(Transaction ID)对应。关联规则在D中的支持度(support)是D中事务同时包含X、Y的百分比,即概率;置信度(confidence)是D中事务已经包含X的情况下,包含Y的百分比,即条件概率。如果满足最小支持度阈值和最小置信度阈值,则认为关联规则是有趣的。这些阈值是根据挖掘需要人为设定。” ——引用百度百科词条解释
百度百科或者一些教材说的太专业了反而很难理解,不妨看下面的个人观点大白话解释:
关联规则提出的背景是购物篮分析,A顾客会买零食、面包、牛奶,不同客户会有不同的消费,那每一个顾客的消费集合就构成了一个事务(消费-支付事务),那这个事务集就上上面说的“唯一标识符TID”;那问题是,每种商品被不同顾客购买了多少次呢?那么这个次数就是“支持频数”,那被所有顾客购买的概率就是“支持度Sup”;那问题又来了,X商品和Y商品之间的被购买关系是怎样的呢?比如消费者买了面包,还可能会买面包伴侣(牛奶等),那面包和牛奶就构成了关联,那这个关联的置信度又是多少呢?就是消费者买了面包,再去买牛奶的概率是多少呢?反之亦言。那这个条件概率,就是上面提到的置信度。
2. 作用:可以揭示数据集的内在的、重要的特性。是很多重要数据挖掘任务的基础关联、相关和因果分析的基本方式。在序列、结构(e.g.子图)模式分析;时空、多媒体、时序和流数据中的模式分析;分类:关联分类;聚类分析:基于频繁模式的聚类;数据仓库:冰山方体计算等各类数据挖掘工作中发挥着基础性作用。
说的又很奇奇怪怪的,关联规则的挖掘到底有什么用?还是可以回到上面的购物篮分析,比如啊,我们分析了面包和牛奶的关联规则之后,如果满足支持度、置信度要求,那么我们就可以把这两个商品放在一块儿(可能会增加购买),或者在做Promotion打造时可以辅助策略制定等等。事实上,从商业视角来说,他就是对People、Place、Promotion、Price策略制定的综合考量因子(4ps战略)。
在和复旦大佬学长交流之后,他提到了异常检测,虽然我也不太明白什么道理。但是结合财会视角来看,这个关联规则或许还能够对企业行为进行监测。那对于网页开发来说,点击哪些模块儿?链接?先后顺序?等都是可以考量的点。
———“个人角度,如果有错误请予以斧正!!!”
3. 挖掘的步骤:①找出频繁项集;②由频繁项集,找出满足minsup和minconfi的关联规则。
如果一个Goodlist由100个商品,如果想要遍历循环,那得到的频繁项集有2^100-1个
↓
引出Apriori算法
二、Apriori-关联规则算法
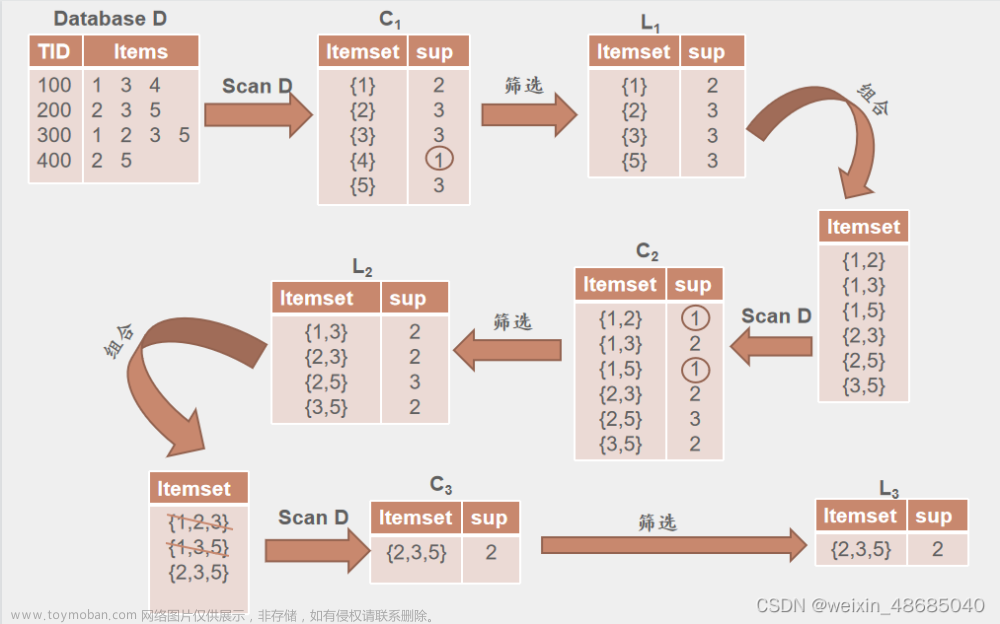
Apriori算法利用频繁项集性质的先验知识(prior knowledge),通过逐层搜索的迭代方法,即将k-项集用于探察(k+1)-项集,来穷尽数据集中的所有频繁项集。
步骤:先找到频繁1-项集集合L1,然后用L1找到频繁2-项集集合L2,接着用L2找L3,直到找不到频繁k-项集,找每个Lk需要一次数据库扫描。最后得到所有满足最小支持的频繁项集合,再进行关联规则输出。
关于Apriori的解释,CSDN中有非常多的前辈给出了自己非常完备的解释,对其优缺点也进行了深入剖析,我在这里就不做过多解释,向大家推我认为非常非常好的三篇文章链接:
这一篇生动有趣,适合年轻人来看!(点击本文字即可)
这一篇有博主手写的解释!适合小白理解Apriori的步骤!
这一篇也不错噢!
三、Apriori算法分解—Python大白话式实现
我看了CSDN中很多博主分享的代码,发现很多博主代码趋同(可能复制粘贴),或者直接调用的外部开源的库来实现的,还有的博主自己撰写的,但是用了很多可能不懂的函数来做的,甚至还有的就直接在一个函数里面嵌套多个函数来传递参数实现,读起来感觉,对小白非常不友好。
那在这里,我就分享一些很简单的代码来实现。包括数据导入、数据处理、调用、关联规则挖掘等完整的分析流程。我看了一下这个应该是全站流程最全面的代码了。
——当然简单就意味着代码很长,有些地方处理的比较粗糙
步骤1: 外部库调用❀
只用到了 pandas itertools 和 自带的time
import pandas as pd #数据导入用
import itertools as it #子集生成用
import time #输出程序员运行时间用步骤2: 数据导入❀
因为是全函数编写,最终的数据导入在代码最后,所以直接拿出来看
if __name__ == '__main__':
# 数据导入
data = pd.read_excel("D:\OneDrive\桌面\测试数据.xlsx", index_col=0, header=0)
data = data.applymap(lambda x: str(x).strip()) # 删除导入时可能存在的空格值,比如:“面包”成了“ 面包”
# 数据格式转换
data = data.values # 改为元组型数据,便于list输出
data = data.tolist() # 输出为客户*商品集合
# 设定支持度和置信度
minsup,minconfi=map(eval,input("请输入支持度和置信度:").split(" "))
start = time.time()
Find_rule_apriori(data,minsup,minconfi)
end=time.time()
print('Running time: {0} Seconds'.format(end - start))步骤3: 数据处理❀
很多博主在数据导入阶段说明不清,不知道最终的导入格式,这里我把测试数据截图放出来仅供大家参考,助于后续程序的理解:

那在Panda导入中会出现一个问题就是,空白格会被默认为None值,输出出来就是“non”:

那么为了处理“nan”值,而常规的pandas的其他功能应该是不能直接删去的,多数还是填充。因此我编写了以下“白话for循环”的Non_deal()函数:
def Non_deal(df):
list_data = []
rows = len(df)
for i in range(0,rows):
list = df[i]
list_con = []
cols = len(list)
for j in range(0,cols):
if list[j]!="nan":
list_con.append(list[j])
#如果用remove法需要倒序去除,否则无法去除干净(因为每一次去除会导致len-1)
list_data.append(list_con)
return list_data输出结果为: 可以看到non值都被删去了。注意remove的使用,我这里处理比较粗糙,为了用Append多加了一个中间列表List_con,虽然用remove会更快。

步骤4:输出所有Goodlist❀
事实上也就是备选频繁1项集,这个函数不太重要,后续调用也完全可以替代别的方式,编写的目的是我思考时的便利逻辑过程的一种方式而已。
#目的是得到备选1-项集
def Good_list(df): #将单个商品集合出来
list_all=[]
list_in=Non_deal(df)
for i in range(0,len(list_in)):
for j in range(0,len(list_in[i])):
list_m=[]
list_m.append(str(list_in[i][j]))
list_all.append(str(list_m))
list_all=list(set(list_all))
for i in range(0,len(list_all)):
list_all[i]=eval(list_all[i])
return list_all步骤5:项集重组❀
因为Apriori是通过满足支持度阈值的频繁k项集得到备选频繁k+1项集合,因此这一个函数的目的便是进行项集重组,升阶化的过程。注意,这个不是放在最前面的逻辑,而是预先编写。为了后面直接调用的准备工作。可以发现也都是for循环,连while等等都不带的。由于我们导入数据就选择的是列表格式,因此我们后续工作也就都利用list来完成,那么list就需要一直for循环调用,不像dict中直接for item in dict等等方便清晰,前面也说了,细节处理还是较粗糙。
#目的是进行k-1-频繁项集合的重组为k项目集合
def creat_connect(list_c,n): ##实现集合内的重组,例如2-项集合重组为3-项集
new_list=[]
for i in range(0,len(list_c)):
list_a = []
for j in range(i+1,len(list_c)):
list_b = list_c[i]
list_d = []
for k in range(0,n):
list_d.append(list_c[j][k])
list_a = list_b+list_d
list_a=list(set(list_a))
list_a.sort()
new_list.append(str(list_a))
new_list=list(set(new_list))
New_list=[]
for i in range(0,len(new_list)):
new_list[i]=eval(new_list[i])
new_list[i].sort()
if len(new_list[i])==n+1:
New_list.append(new_list[i])
return New_list步骤6:支持度扫描与输出 ❀
这里就回归了逻辑线条,这里提供两种方法,一种是输出counts一种是输出rates,即支持频数和支持度的两种衡量办法,这里仅供大家挑选,两个函数没什么区别。 本find_rule函数用的是counts函数,如果要换记得调整为rates。
#输出每个k-项频繁集的候选集的比率
def sup_rate(df,data):
m = len(data) # 事务总数
item_set_list = []
for i in range(0,len(df)):
n=0
list_n=[]
for j in range(0,len(data)):
if (set(df[i]) <= set(data[j]))==True:
n+=1
list_n.append(df[i])
list_n.append(round(n/m,2))
item_set_list.append(list_n)
return item_set_list
#输出每个k-项频繁集的候选集的个数,上有比率写法,两者无本质区别,都可以使用
def sup_counts(df,data): #输出每个1-项频繁集的候选集的次数
item_set_list = []
for i in range(0,len(df)):
n=0
list_n=[]
for j in range(0,len(data)):
if (set(df[i]) <= set(data[j]))==True:
n+=1
list_n.append(df[i])
list_n.append(n)
item_set_list.append(list_n)
return item_set_list步骤7:根据最小支持度阈值进行减枝叶❀
其他博主文章也说过,Apriori算法的核心就是通过剪枝来减少扫描难度。因为非频繁项集的超级也一定不频繁。
#得到满足最小支持度阈值的关联规则(find——rule of min-sup-rate item)
def sup_satisfy_item(data,min_suprate):
n = len(data) # 事务总数
Good_list1=Good_list(data)
m = len(Good_list1) # 商品总数
dt = sup_counts(Good_list1, data)
All_freitem_list=[]
for k in range(1,m):
dt.sort()
k_apriori=[]
for j in range(0,len(dt)):
if dt[j][-1] >= min_suprate*n: ##减枝过程
k_apriori.append(dt[j][0])
k_apriori.sort()
dt=sup_counts(creat_connect(k_apriori,k),data)
if len(k_apriori)!=0:
All_freitem_list.append(k_apriori)
else:
break
return All_freitem_list步骤8:对每一个频繁项集进行子集拆分计算confi和rule挖掘❀
这个函数也是一个中间函数,预备工作而已。注意条件(前提是频繁项集,如果不是的话,数量可能非常多,很难挖掘 )这也是身边其他人或者大家可能会犯的错误,为啥不通过Good_list清单来生成所有的1/2/3/.../k项备选频繁集,再来扫描其每一个的支持度呢?那如果是这么想的,就忽略了Apriori算法的核心了。具体是什么可以返回自行理解。
——好吧我承认 /(ㄒoㄒ)/~~:事实上Good_list()函数的编写,就是我按照上述逻辑来编写的
def Ksubset_get(df): #获得非空子集(前提条件是频繁项集,否则数量太多,很难挖掘)
n =len(df)
k =len(df[0])
All_nzsubset=[]
for num in range(n):
for i in it.combinations(df,num+1): #调用it.combination 函数
All_nzsubset.append(list(i))
return All_nzsubset步骤9:Find_rule❀
最后一步了!!直接进行规则输出就好了,这一步非常非常非常的复杂,因为用的是list不是dict,可能在某些处理上不得不加入很多中间list来进行暂存以便后续调用。但其实我后面想了一下,用dict也很复杂,简单不到哪里去的感觉。(主要是没写)
def Find_rule_apriori(data,min_suprate,min_confi):
a=len(data) #事务总数
Sup_satisfy_item=sup_satisfy_item(data,min_suprate) #获得满足支持度的频繁项集,第一项为频繁1项集合的集合,以此类推。
l=len(Sup_satisfy_item) #获得频繁项集集合的集合长度
for i in range(1,l): #无需对频繁1项集合找寻关联规则,直接从频繁二项集的集合进行扫寻循环
Sup_satisfy_itemi=Sup_satisfy_item[i] #得到一个频繁i+1项集合的列表的列表
m=len(Sup_satisfy_itemi)
for j in range(0,m): #为对每一个频繁项集进行扫寻,因此需要再做一次for循环
Prule = Sup_satisfy_itemi[j]
list1=[]
list1.append(Prule)
item_counts1 = sup_counts(list1,data)[0][-1] #首先需要得到这一个频繁项集的支持度,或者计算频数也可以
list1.clear()
prerule_find = Ksubset_get(Prule) #得到这一个频繁项集集合的所有非空集合,方便进行关联规则的重组
prerule_find.remove(prerule_find[-1]) #删除全集
q = len(prerule_find) #得到排除全集后的关联重组列表的长度,以便进行for循环
for z in range(0,q):
list2=[]
list2.append(prerule_find[z])
item_counts2 = sup_counts(list2,data)[0][-1] #得到每一个关联重组后项集的支持度(或频数)
list2.clear()
if item_counts2 > 0:
Confi_item = item_counts1/item_counts2 #得到置信度
if Confi_item >= min_confi: #置信度减除
n=len(prerule_find[z])
list3 = Prule[:]
for o in range(0, n):
list3.remove(str(prerule_find[z][o]))
print("{0} ==> {1},sup={2},confi={3}".format(prerule_find[z],list3,round(item_counts1/a,2),round(Confi_item,2)))输出结果:可以看到,整个程序的运行速度还是比较快的,加入更多的good和tid之后个人认为还是可以保持较快的输出速度。

四、Apriori代码——全部呈上~
import pandas as pd
import numpy as np
import itertools as it
import time
# 去除集合矩阵(i,j)None值,便于计数以及算法,常规的pandas是用来数据清洗和数据填充的,没办法解决这种问题
def Non_deal(df):
list_data = []
rows = len(df)
for i in range(0,rows):
list = df[i]
list_con = []
cols = len(list)
for j in range(0,cols):
if list[j]!="nan":
list_con.append(list[j]) #如果用remove法需要倒序去除,否则无法去除干净(因为每一次去除会导致len-1)
list_data.append(list_con)
return list_data
#目的是得到备选1-项集
def Good_list(df): #将单个商品集合出来
list_all=[]
list_in=Non_deal(df)
for i in range(0,len(list_in)):
for j in range(0,len(list_in[i])):
list_m=[]
list_m.append(str(list_in[i][j]))
list_all.append(str(list_m))
list_all=list(set(list_all))
for i in range(0,len(list_all)):
list_all[i]=eval(list_all[i])
return list_all
#目的是进行k-1-频繁项集合的重组为k项目集合
def creat_connect(list_c,n): ##实现集合内的重组,例如2-项集合重组为3-项集
new_list=[]
for i in range(0,len(list_c)):
list_a = []
for j in range(i+1,len(list_c)):
list_b = list_c[i]
list_d = []
for k in range(0,n):
list_d.append(list_c[j][k])
list_a = list_b+list_d
list_a=list(set(list_a))
list_a.sort()
new_list.append(str(list_a))
new_list=list(set(new_list))
New_list=[]
for i in range(0,len(new_list)):
new_list[i]=eval(new_list[i])
new_list[i].sort()
if len(new_list[i])==n+1:
New_list.append(new_list[i])
return New_list
#输出每个k-项频繁集的候选集的比率
def sup_rate(df,data):
m = len(data) # 事务总数
item_set_list = []
for i in range(0,len(df)):
n=0
list_n=[]
for j in range(0,len(data)):
if (set(df[i]) <= set(data[j]))==True:
n+=1
list_n.append(df[i])
list_n.append(round(n/m,2))
item_set_list.append(list_n)
return item_set_list
#输出每个k-项频繁集的候选集的个数,上有比率写法,两者无本质区别,都可以使用
def sup_counts(df,data): #输出每个1-项频繁集的候选集的次数
item_set_list = []
for i in range(0,len(df)):
n=0
list_n=[]
for j in range(0,len(data)):
if (set(df[i]) <= set(data[j]))==True:
n+=1
list_n.append(df[i])
list_n.append(n)
item_set_list.append(list_n)
return item_set_list
#得到满足最小支持度阈值的关联规则(find——rule of min-sup-rate item)
def sup_satisfy_item(data,min_suprate):
n = len(data) # 事务总数
Good_list1=Good_list(data)
m = len(Good_list1) # 商品总数
dt = sup_counts(Good_list1, data)
All_freitem_list=[]
for k in range(1,m):
dt.sort()
k_apriori=[]
for j in range(0,len(dt)):
if dt[j][-1] >= min_suprate*n: ##减枝过程
k_apriori.append(dt[j][0])
k_apriori.sort()
dt=sup_counts(creat_connect(k_apriori,k),data)
if len(k_apriori)!=0:
All_freitem_list.append(k_apriori)
else:
break
return All_freitem_list
def Ksubset_get(df): #获得非空子集(前提条件是频繁项集,否则数量太多,很难挖掘)
n =len(df)
k =len(df[0])
All_nzsubset=[]
for num in range(n):
for i in it.combinations(df,num+1): #调用it.combination 函数
All_nzsubset.append(list(i))
return All_nzsubset
def Find_rule_apriori(data,min_suprate,min_confi):
a=len(data) #事务总数
Sup_satisfy_item=sup_satisfy_item(data,min_suprate) #获得满足支持度的频繁项集,第一项为频繁1项集合的集合,以此类推。
l=len(Sup_satisfy_item) #获得频繁项集集合的集合长度
for i in range(1,l): #无需对频繁1项集合找寻关联规则,直接从频繁二项集的集合进行扫寻循环
Sup_satisfy_itemi=Sup_satisfy_item[i] #得到一个频繁i+1项集合的列表的列表
m=len(Sup_satisfy_itemi)
for j in range(0,m): #为对每一个频繁项集进行扫寻,因此需要再做一次for循环
Prule = Sup_satisfy_itemi[j]
list1=[]
list1.append(Prule)
item_counts1 = sup_counts(list1,data)[0][-1] #首先需要得到这一个频繁项集的支持度,或者计算频数也可以
list1.clear()
prerule_find = Ksubset_get(Prule) #得到这一个频繁项集集合的所有非空集合,方便进行关联规则的重组
prerule_find.remove(prerule_find[-1]) #删除全集
q = len(prerule_find) #得到排除全集后的关联重组列表的长度,以便进行for循环
for z in range(0,q):
list2=[]
list2.append(prerule_find[z])
item_counts2 = sup_counts(list2,data)[0][-1] #得到每一个关联重组后项集的支持度(或频数)
list2.clear()
if item_counts2 > 0:
Confi_item = item_counts1/item_counts2 #得到置信度
if Confi_item >= min_confi: #置信度减除
n=len(prerule_find[z])
list3 = Prule[:]
for o in range(0, n):
list3.remove(str(prerule_find[z][o]))
print("{0} ==> {1},sup={2},confi={3}".format(prerule_find[z],list3,round(item_counts1/a,2),round(Confi_item,2)))
if __name__ == '__main__':
# 数据导入
data = pd.read_excel("D:\OneDrive\桌面\测试数据.xlsx", index_col=0, header=0)
print(data)
data = data.applymap(lambda x: str(x).strip()) # 删除导入时可能存在的空格值,比如:“面包”成了“ 面包”
# 数据格式转换
data = data.values # 改为元组型数据,便于list输出
data = data.tolist() # 输出为客户*商品集合
print(Non_deal(data))
# 设定支持度和置信度
minsup,minconfi=map(eval,input("请输入支持度和置信度:").split(" "))
start = time.time()
Find_rule_apriori(data,minsup,minconfi)
end=time.time()
print('Running time: {0} Seconds'.format(end - start))
五、总结
① 非常感谢我们老师的指导和激励呜呜呜,上课一直被点名。
② Apriori算法真的很难写出来,写的很痛苦的家人们一定不要放弃!心态要好,希望这篇文章能够帮到你们一些,给到你们一些“我踩过的坑不要踩”的建议。
③ 个人一直以来就喜欢分享,看以前的文章也可以发现,什么聚类分析、模糊聚类(传递闭包矩阵算法等等)都是个人编写的大白话函数,所以撰写本文的初衷就是个人的分享~
④ K-means算法本人由于之前学习数学建模的时候太懒了,就没有撰写。
⑤ 如果大家复制了我的函数,希望能够在代码段中标明了引用。
⑥ 本文在细节的处理非常粗糙,希望大家在编写过程中能够予以改进,期待和各位交流(改进了一定要记得和我分享分享呜呜呜)文章来源:https://www.toymoban.com/news/detail-822138.html
⑦ 这是一个学习锻炼的过程,非计科、信管等专业,但也要强化这种语言能力~特别是商科!文章来源地址https://www.toymoban.com/news/detail-822138.html
到了这里,关于【商业挖掘】关联规则——Apriori算法(最全~)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!