数据结构预习笔记第一章-数据结构的概念-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构预习笔记第一章-数据结构的概念。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据结构 “预习” 笔记：第一章数据结构的概念

一、学习目标

重点理解数据结构的定义，逻辑结构，存储结构，算法的时间效率分析和算法的空间效率分析

二、数据结构概念知识

2.1 什么是数据结构

概念😵

数据：所有的数字，字符和能够被输入到计算机中进行运算的符号的集合。

数据元素：数据元素是数据的基本单位❗️，在计算机中通常是作为整体进行处理的.一个数据的元素可以由多个数据项组成。

数据项：数据的最小单位❗️，数据项是不可分割的。同时数据项也被称为成员或者域

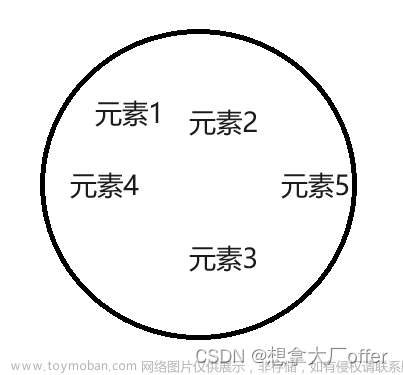
数据结构：相互之间存在着特定关系的数据元素的集合。在这门课程中常常讨论的数据结构有：相邻关系和邻接关系

数据结构包括以下三个方面：

逻辑结构：数据元素之间的逻辑关系，这部分面向用户，与计算机无关。可以使用树或者图等等用户容易理解的方式进行展示。其分为两种类型：线性和非线性

物理结构: 面向计算机的，对于逻辑结构的存储的表示。常见的存储的方式有：顺序存储、链式存储、索引存储、散列存储。

数据运算: 针对于数据进行的运算或者处理。

My理解😏

用图表对于这里的概念进行理解，当前的表即可以理解为逻辑结构。那么表的存储可以理解为物理结构。若是想要对于表中的数据进行操作，便可以算是数据运算。

2.2 抽象数据类型ADT（Abstract Data Type）

概念😵

数据类型：程序设计语言中已经实现的数据结构。一组数据的值和对这组数据执行的操作的集合的总称。

抽象数据类型ADT：数据元素集合以及在这些数据上的操作被称做抽象数据类型。与具体的存储和具体实现算法无关。数据声明和数据运算分离。其可以定义一个完整的数据结构。

My理解😏

简单的数据类型包括整数、浮点数、字符、布尔值等。每个数据类型有其特定的性质和能够执行的操作。
常见的抽象数据类型包括栈、队列、链表、树、图等。这些抽象数据类型为程序员提供了一种高层次的抽象，使得可以在不关心底层实现的情况下使用数据结构。

举例来说，栈是一种抽象数据类型，它定义了一组操作，如压栈（push）、弹栈（pop），但并没有规定这些操作的具体实现方式。程序员可以使用栈来解决问题，而无需关心栈的具体实现。

三、算法与算法评价概念知识

3.1 什么是算法

概念😵

算法是解决问题或执行特定任务的有限步骤的有序集合。简而言之，算法是一种清晰定义、可执行的计算过程，它接受输入数据、通过一系列的计算步骤处理这些数据，并最终产生输出结果。

3.2 算法的特性

概念😏

有穷性 ：算法必须在有限步骤内终止。这意味着算法的执行过程不能无限循环或永不停止。有穷性确保算法对于输入的任何有限数据集都能够在有限的时间内执行完毕。

确定性 ：算法的每个步骤必须具有明确定义的操作，且对于相同的输入，算法的执行过程必须总是产生相同的输出。确定性保证了算法的可预测性和可控性。

可行性 ：算法必须是可行的，也就是说，它必须能够解决指定问题的实例。算法的任务是找到问题的解决方案，这意味着算法必须在给定的约束条件下能够产生正确的输出。

无二义性 ：算法的每个步骤必须准确描述，让计算机知道每个指令要求完成什么。

输入：算法接受输入，这是算法开始执行时所需的信息。输入是指算法处理的数据或信息。输入可以是0个，也可以是多个。❗️。

输出：算法生成输出，这是算法在执行完毕后产生的结果。输出是算法最终解决问题的体现。输出可以是1个也可以是多个。❗️

3.3 评价好算法的四个标准

概念😮

正确性 ：正确性是指算法或程序执行的结果是否符合预期。一个正确的算法应该能够在给定输入条件下产生正确的输出。

可读性 ：可读性指的是代码的清晰度和易读性。可读性好的代码更容易被人理解和维护。

通用性 ：通用性表示算法或程序的适用范围广泛，不仅能够解决特定问题，还能够应用于更广泛的场景。

健壮性：健壮性是指算法或程序对于异常情况的处理能力。一个健壮的程序能够在面对非预期的输入或操作时保持稳定运行，而不会导致崩溃或产生不可预测的结果。

3.4 算法的评价方法

事后分析统计方法 ：
- 对于算法编写对于的程序，并进行运行，统计其执行的时间。
- 但是受数据源，硬件设备严重的影响，比较结果很难用来衡量算法的优劣。
事前分析统计方法 ：
- 不考虑算法执行后的其他因素的干扰，只对于当前的问题的规模，算法策略和方法等关键因素进行统计。

3.5 算法效率的度量

概念😮

时间复杂度：

时间复杂度是评估算法运行效率的概念。它描述了算法的运行时间和输入规模n之间的关系。当问题规模由1到n时，解决问题的算法的CPU时间也从g(1)到g(n)。则成算法的时间代价是g(n)

空间复杂度：

空间复杂度是一种用于评估算法所需的存储空间与输入规模之间关系的概念。当问题规模由1到n时，解决问题的算法所需占用的内存空间也以某种单位从f(1)到f(n)，此时称算法的空间代价是f(n)。

大O表示法：

定义: 若存在常量 $c$ 和 $n_0$ ，对于任意的 $n>n_0$ 有 $\leq c \cdot f(n)$ 则认为： $\leq O({f(n)})$

则 $O({f(n)})$ 被称为算法复杂度

My理解😃

时间复杂度和空间复杂度都可以来表示算法的算法复杂度。所以说他们都可以用大O表示法进行表示。

大O表示法举例:

$f (n)$ $O({f(n)})$

$n$ $O (n)$

$n + 2$ $O (n)$

$n^2 + n + 17$ $O(n^2)$

$2n^2 + n + 2$ $O(n^2)$

$2^n + n + 2$ $O(2^n)$

$\sqrt{n+3}$ $O(\sqrt{n})$

😏发现了什么？当前的 $f (n)$ 和 $O({f(n)})$ 之间，前者总是小于常数倍的后者

比如： $\leq 2n$ ， $n^2 + n + 17 \leq 2n^2$ ， $\sqrt{n+3} \leq \sqrt{2n}$

那么根据大O表示法的定义，就可以得到上表的表示。😎

$f (n)$	$O({f(n)})$
$n$	$O (n)$
$n + 2$	$O (n)$
$n^2 + n + 17$	$O(n^2)$
$2n^2 + n + 2$	$O(n^2)$
$2^n + n + 2$	$O(2^n)$
$\sqrt{n+3}$	$O(\sqrt{n})$

3.6 常用的度量和度量间的关系

常见的度量😘

$O({f(n)})$	名称
$O (1)$	常量复杂度
$O (n)$	线性复杂度
$O(n^2)$	平方复杂度
$O(log_2{n})$	对数复杂度
$O(n^3)$	立方复杂度
$O(2^n)$	指数复杂度

度量之间的关系💖

$O(\log_2{n}) < O(\sqrt{n})<O(n) < O(n{\log_2{n}}) < O(n^2) < O(n^3) < O(2^n) < O(n!)$

四、算法和算法评价之实战演练

基础概念🙃

加法规则:

$T(n) = T_1(n) + T_2(n) = O(f_1(n))+O(f_2(n)) = O({ max(f_1(n),f_2(n)} ))$

乘法规则:

$T(n) = T_1(n)*T_2(n) = O(f_1(n))*O(f_2(n)) = O(f_1(n)*f_2(n))$

My理解🤤

加法规则在循环不嵌套的时候使用，取复杂度的最大值

乘法规则在循环中，循环嵌套时，进行乘积运算

当然这难以理解。下面是时间复杂度的例子，本质上时间复杂度就是CPU执行语句消耗的时间

在这个思路上我们继续分析下述代码😏
// 假设CPU按照"行"进行执行 每一行执行时间是一样的
// 遇到循环的时候，把循环展开成行 
int main(){
    // 1. 一次 一行 
    int n; 
    cin>> n; 
    int s1 = 0;
    int s2 = 0;
    // 2. 下述循环可以展开为 N次 N行 
    for(int i=0;i<n;i++)  
    {
        s1+=2;
    }
    // 4. 所以下述循环就是 N*N次 N*N行 
    for(int i=0;i<n;i++)
    {
        // 3. 下述循环展开为 N次 N行
        // 每一个循环都是 N次 N行 
        for(int j=0;j<n;j++)
        {
            s2++; 
        }
    }
}
那么对于以上的代码而言，运行的时间复杂度是多少呢？

当我们幻想着把所有的代码展开的时候就有： $4 + N + N^2$ ，对于大O表示法： $4 + N + N^2 < 2N^2$ 。

根据定义，时间复杂度就是 ~ $O(n^2)$

这样看来，原来的两个规则就很好理解了。😄

加法规则

把上述的代码拆成3段： $T_1(n)=4$ ， $T_2(n)=N$ ， $T_3(n)=N^2$

对应的时间复杂度: $O_1(n)=1$ ， $O_2(n)= N$ ， $O_3(n)=N^2$

所以：由于他们循环不嵌套: 取最大值，得到时间复杂度还是 ~ $O(n^2)$

乘法规则

得自己品下😛

Tips:对于上面的两个循环由于是嵌套关系,对于第一个循环有 $O_1(n) = N$ ，第二个循环有 $O_2(n)=N$

那么对于这里的代码片段而言，由于他们循环嵌套: 取乘积，得到时间复杂度是 ~ $O(n^2)$

会爬了，该起飞了🤡:

实际上，上述的核心思想是：计算了CPU一共执行了多少行。

解题步骤如下：

对于代码进行分段：依据循环进行分段，只考虑最外层。

解循环：将循环中的递减逻辑想象为递增逻辑

计算循环的时间复杂度：

执行假设：假设当前循环运行到了最后一步，并且执行了 $X$ 次

条件求解：找到一个满足退出循环的关系式。得到时间复杂度 $T$

乘法规则求解：同样的方法对于内部的循环进行求解，必要时，保留上层循环的最后一步的值。所有值进行乘法求解。

加法规则求解：同样的方法作用于每一个程序段。

答案：根据度量之间的关系进行最终答案的编写
ps：此处方法有待考究，简答勿用😏

示例

用法

假设有下面的这段代码：
int main(){
    // 代码分段: 第一段 
    int n;
    int s = 0; 
    cin>> n;
    int x = n*n;
    // 代码分段: 第二段
    for(int i=n-1;i>1;i--)
    {
        s++;
    };
    // 代码分段: 第三段
    while(x!=1)
    {
        x = x * 2;
    };
    // 代码分段: 第四段
    for(int k=1;k<=n;k*=2){
        for(int j=1;(j+1)*(j+1)<=n;j++)
        {
            s++;
        }
    };
}
对于代码进行分段：如上所示，只关注最外层的循环，代码被分为四段

解循环：对于第二段的递减逻辑，可以写为如下的递增逻辑
for(int i=2;i<=n-1;i++)
{
    s++;
};
计算循环内的时间复杂度
// 代码分段: 第二段
for(int i=2;i<=n-1;i++)
{
    s++;
};
执行假设:(执行后的值)

循环执行0次时：循环内i = 2（ps：初始值为2）
循环执行1次时：循环内i = 3
循环执行2次时：循环内i = 4
循环执行X次时: 循环内i=X+2

条件循环:

当程序运行刚好结束时，此时满足：

$X + 2 = n - 1$

😃

解得： $X = n - 3$

那么时间复杂度就是 $O (n)$ 😏

// 代码分段: 第三段
x = n*n;
while(x!=1)
{
    x = x * 2;
};
执行假设:(执行后的值)

循环执行0次时：循环内 $x=n^2$ （ps：初始值 $n^2$ ）
循环执行1次时：循环内 $x={n^2 \over 2}$
循环执行2次时：循环内 $x={n^2 \over 4}$
循环执行X次时: 循环内 $x={n^2 \over 2^X}$

条件循环:

当程序运行刚好结束时，此时满足：

${n^2 \over 2^X} = 1$

😃

解得： $X = 2log_2n$

那么时间复杂度就是 $O(log_2n)$ 😏

// 代码分段: 第四段
for(int k=1;k<=n;k*=2){
    for(int j=1;(j+1)*(j+1)<=n;j++)
    {
        s++;
    }
};
这是个双重循环😱看起来好逆天

第一重循环

执行假设:

循环执行0次时：循环内 $k = 1$ （ps：初始值 $1$ ）
循环执行1次时：循环内 $k = 2$
循环执行2次时：循环内 $k = 4$
循环执行X次时: 循环内 $k=2^x$

条件循环:

当程序运行刚好结束时，此时满足：

$2^x = n$

😃

解得： $X = log_2n$

那么时间复杂度就是 $T_1 = O(log_2n)$ 😏

结束了？NONONO🤡

第二重循环

执行假设:

循环执行0次时：循环内 $j = 1$ （ps：初始值 $1$ ）
循环执行1次时：循环内 $j = 2$
循环执行2次时：循环内 $j = 3$
循环执行X次时: 循环内 $j = X$

条件循环:

当程序运行刚好结束时，此时满足：

${(X+1)}^2 < n$

😃

解得： $\sqrt{n} -1$

那么时间复杂度就是 $T_2 = O(\sqrt{n})$ 😏

结束了？NONONO🤡
乘法规则求解

$O(\sqrt{n} \cdot log_2n)$

最后一步：加法规则求解

取最大值！

所以程序的时间复杂度为:

$O(\sqrt{n} \cdot log_2n)$

五、补充

5.1 最好，最坏，平均时间复杂度

基础概念🙃

最好时间复杂度:最好时间复杂度是指在最理想情况下，算法执行所需的最小时间。

最坏时间复杂度:最坏时间复杂度是指在最不利情况下，算法执行所需的最大时间。

平均时间复杂度:平均时间复杂度是指算法在所有可能输入情况下执行所需时间的期望值。

My理解

类似于猜数字游戏：最好就是一次猜中，最坏就是碰巧避开了正确答案😅最后才猜中。平均就是期望，就是猜的次数足够多的情况下逐渐趋近的那个值就是期望值。

5.2 空间复杂度

可以参考下大佬的文章😍

空间复杂度计算

(ps: 学渣老哥不想考试~奈何大四不得不预习下😝)文章来源地址https://www.toymoban.com/news/detail-822315.html

到了这里，关于数据结构预习笔记第一章-数据结构的概念的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

数据结构预习笔记第一章-数据结构的概念

数据结构 “预习” 笔记：第一章数据结构的概念

一、学习目标

二、数据结构概念知识

2.1 什么是数据结构

2.2 抽象数据类型ADT（Abstract Data Type）

三、算法与算法评价概念知识

3.1 什么是算法

3.2 算法的特性

3.3 评价好算法的四个标准

3.4 算法的评价方法

3.5 算法效率的度量

3.6 常用的度量和度量间的关系

四、算法和算法评价之实战演练

五、补充

5.1 最好，最坏，平均时间复杂度

5.2 空间复杂度

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2

数据结构预习笔记第一章-数据结构的概念

数据结构 “预习” 笔记：第一章 数据结构的概念

一、学习目标

二、数据结构概念知识

2.1 什么是数据结构

2.2 抽象数据类型ADT（Abstract Data Type）

三、算法与算法评价概念知识

3.1 什么是算法

3.2 算法的特性

3.3 评价好算法的四个标准

3.4 算法的评价方法

3.5 算法效率的度量

3.6 常用的度量和度量间的关系

四、算法和算法评价之实战演练

五、补充

5.1 最好，最坏，平均时间复杂度

5.2 空间复杂度

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2

数据结构 “预习” 笔记：第一章数据结构的概念