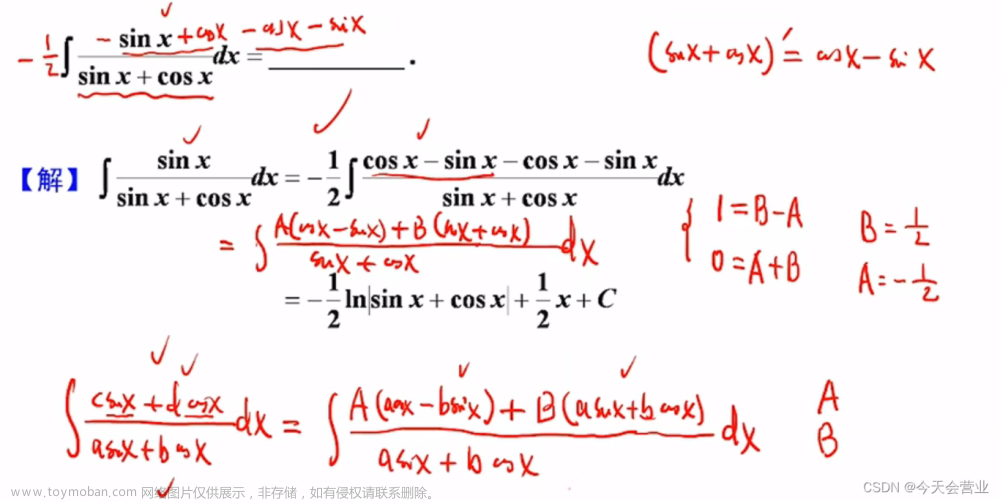第五课上《积分-不定积分》
1/6 直接套公式算不定积分
⑧ ∫ t a n x d x = ∫ s i n x c o s x d x = ∫ 1 c o s x d ( − c o s x ) = − l n ∣ c o s x ∣ + C ⑨ ∫ c o t x d x = ∫ 1 t a n x d x = ∫ c o s x s i n x d x = ∫ 1 s i n x d ( s i n x ) = l n ∣ s i n x ∣ + C ( t a n x ) ‘ = s e c 2 x , t a n 2 x + 1 = s e c 2 x [ 十七 ] ∫ d x a 2 + x 2 = ∫ d x a 2 ( 1 + ( x / a ) ) 2 = ∫ d ( x / a ) a ( 1 + ( x / a ) ) 2 = 1 a a r c t a n ( x a ) + C [ 十六 ] ∫ d x a 2 − x 2 = ∫ d x a 1 − ( x / a ) 2 = ∫ d ( x / a ) 1 − ( x / a ) 2 = a r c s i n ( x / a ) + C [ 二十 ] 令 x = a t a n x 和 x = a s e c x 【具体参考张宇基础 30 讲 P 110 】 ⑧ \int tanx dx=\int \frac{sinx}{cosx} dx =\int \frac{1}{cosx} d(-cosx)=-ln|cosx|+C \\ ⑨ \int cotx dx=\int \frac{1}{tanx} dx =\int \frac{cosx}{sinx} dx=\int \frac{1}{sinx} d(sinx)=ln|sinx|+C \\ (tanx)^`=sec^2x,tan^2x+1=sec^2x \\ [十七] \int \frac{dx}{a^2+x^2}=\int \frac{dx}{a^2(1+(x/a))^2}=\int \frac{d(x/a)}{a(1+(x/a))^2}=\frac{1}{a}arctan(\frac{x}{a})+C \\ [十六] \int \frac{dx}{\sqrt{a^2-x^2}}=\int \frac{dx}{a\sqrt{1-(x/a)^2}}=\int \frac{d(x/a)}{\sqrt{1-(x/a)^2}}=arcsin(x/a)+C \\ [二十] 令x=atanx和x=asecx\\ 【具体参考张宇基础30讲P110】 ⑧∫tanxdx=∫cosxsinxdx=∫cosx1d(−cosx)=−ln∣cosx∣+C⑨∫cotxdx=∫tanx1dx=∫sinxcosxdx=∫sinx1d(sinx)=ln∣sinx∣+C(tanx)‘=sec2x,tan2x+1=sec2x[十七]∫a2+x2dx=∫a2(1+(x/a))2dx=∫a(1+(x/a))2d(x/a)=a1arctan(ax)+C[十六]∫a2−x2dx=∫a1−(x/a)2dx=∫1−(x/a)2d(x/a)=arcsin(x/a)+C[二十]令x=atanx和x=asecx【具体参考张宇基础30讲P110】
2/6 设一部分再算的不定积分
换元法
【补充：凑微分法】
3/6 多项相加的不定积分
4/6 两项相乘的不定积分
【具体参考张宇基础 30 讲 P 112 】 【具体参考张宇基础30讲P112】 【具体参考张宇基础30讲P112】
5/6 sin、cos相乘的不定积分
c o s 2 x = c o s 2 x − s i n 2 x = 2 c o s 2 x − 1 = 1 − 2 s i n 2 x cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x cos2x=cos2x−sin2x=2cos2x−1=1−2sin2x文章来源：https://www.toymoban.com/news/detail-822961.html
6/6 x2加减常数项的不定积分
文章来源地址https://www.toymoban.com/news/detail-822961.html
到了这里，关于高数【积分-不定积分】--猴博士爱讲课的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
