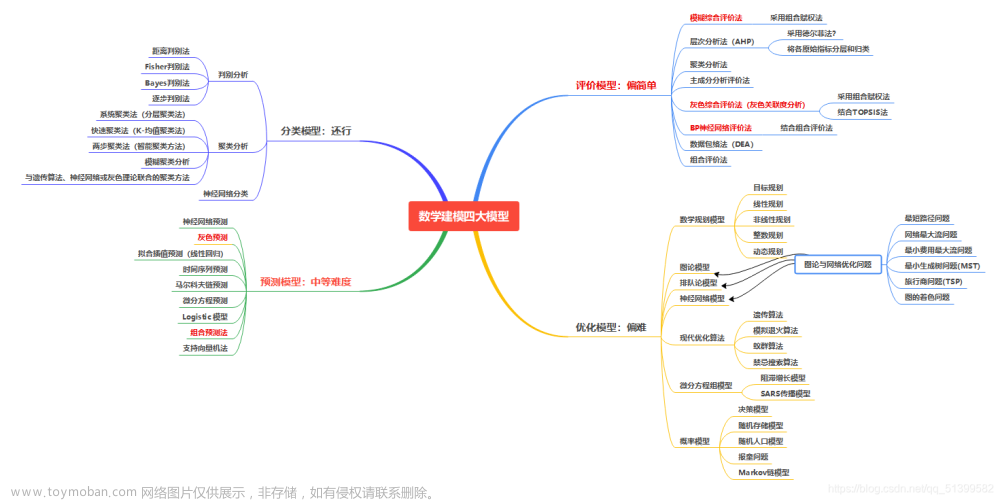
一、模型引出
1、问题的提出
层次分析法是评价决策类中一个比较常用的方法,很多留意美赛赛题的小伙伴们就会发现,在美赛EF类题目的历年O奖论文中,层次分析法出现的概率是非常高的。层次分析法呢一般是针对评价决策类的题目,让我们评价或选择一个可能更好、更优的政策及方案,那这样呢,我们就要先找到衡量政策和方案好坏的一些指标,然后呢再去量化这些指标,量化指标之后,我们再去找到一个评价体系,综合考虑所有的指标来看哪一个政策更好。
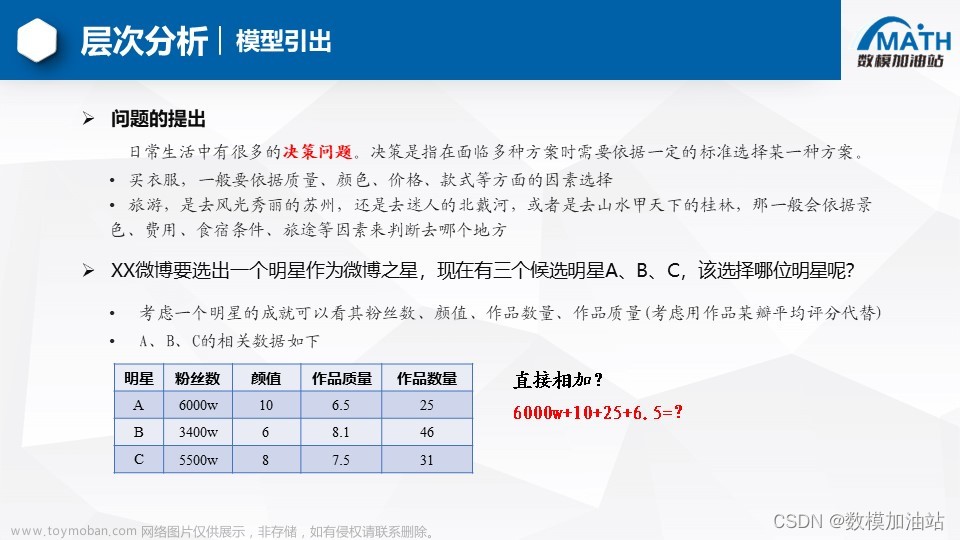
这里呢,给大家举一个例子,比如说某某微博要选一个明星,作为微博之星,现在呢有三个候选人ABC,那我们应该选择哪位明星呢,应该要找哪几个指标来衡量,比如说呢这里我们考虑明星的粉丝数,颜值,作品数量和作品质量。我们来看ABC这三位明星的相关数据。

那这里呢我们就引出一个概念,怎么能让这个指标划到同一个数量级,且保证同一指标内它的排名和这个差距不变,有一个方法呢叫做归一化处理,我们把ABC3位明星的各项指标,进行归一化处理,然后相加就可以得到三位明星对应的得分,实际上呢除了这个归一化处理,我们还要考虑一个因素,就是他每一个指标在进行这个选择的时候,它的重要程度是不同的,所以说呢我们怎么去判断这个重要性呢,我们就要给这每个指标加上一个权重,那在这里呢这个权重是我随意设置的,他肯定是不够科学,那么我们如何能够科学的设定这个权重呢,其实呢这就是层次分析法的主要作用了。
2、基本概念
层次分析法呢简称AHP,它是对一些比较复杂,较为模糊的问题做出决策的简易方法,它就适用于那些难以完全定量分析的问题,它是由美国的运筹学家萨吉教授,于上世纪70年代提出的一种方法,那这种方法呢它并不代表着我们绝对的客观,而是说它在我们相对随意的啊,去制定权重的情况下,又多了一份科学的东西,其实呢层次分析法,它并不是一个非常客观的定弦方法,但是相比我们随意的去设置权重,它还是更为科学的,那我们应该怎样去运用层次分析法呢。
二、模型原理
1、原理
在应用层次分析法解决问题时,我们首先要把问题进行条理化,层次化,然后构造出一个有层次的结构模型,我们可以看一下图片右下角,这个结构模型呢分为三层,分别是目标层,准则层和方案层,那第一层呢也就是目标层,它只有一个元素,它是分析问题的预定目标或者说理想结果,那中间层呢,它包含了实现目标所涉及的中间环节,其实呢就是我们判断一个方案好坏的,然后最底层呢叫做方案层,它就为实现目标提供了可供选择的措施和方案,好的那我们知道了层次分析法的一个结构模型,我们应该怎样去解决题目呢。

2、基本步骤
首先它有一个基本步骤,第一个步骤呢叫做建立递阶层次结构模型,也就是我们刚刚这个模型,那么刚刚那个选出微博之星的模型,已经很清晰了,第一层呢就是选出微博之星,那这准则层呢其实就是粉丝,还有作品质量等等,那方案层呢就是ABC3个人,第二步就是构造出各个层次所有的判断矩阵,然后构造出判断矩阵之后,我们要进行一致性检验,那最后就是求出权重,然后把指标按照权重进行综合评分。那我们现在来套用这四个步骤来选择微博之星。(详细的课程教程请关注b站up数模加油站,进行学习)
三、典型例题
1、建立递阶层次结构模型及判断矩阵
首先是建立递阶层次结构模型,那层次模型呢就如这个图所示,那这个层次结构一目了然,接下来我们就要构造出各层次中的判断矩阵。

2、构造判断矩阵
什么叫做判断矩阵呢,我们对所有的指标进行两两比较,然后就能构造出判断矩阵,矩阵中的元素,我们用aij来代表,那aij是什么意思呢,aij代表的意思就是,第i个指标相对于第j个指标的重要程度,好的,现在呢我们来尝试构造判断矩阵,我们依次对所有的指标进行两两比较,就会得到完整的判断矩阵啊,就是途中的一个表,那实际上呢我们在构造判断矩阵的过程中,每次都是两两比较,在两两比较的过程中呢,是不涉及其他的因素和指标的,那如果比较的指标比较多,就有可能会导致最后的结果出现矛盾,那应该怎么办呢,这个时候我们就引入了一个概念,叫做一致性检验。


3、一致性检验
(1)一致性检验原理
什么是一致性检验呢,一致性检验,就是来看看我们判断矩阵中的各个指标,它的重要程度是否一致,比如说刚刚那种情况下,这个质量它的重要程度是不是一会儿是重要的,一会儿又是不重要的,那它就是不一致的。(详细的课程教程请关注b站up数模加油站,进行学习)


(2)一致性检验的步骤

(3)一致性检验计算
我们来计算判断矩阵的最大特征值,来求得CR和RI,当前的判断矩阵呢,我们发现CR大于0.1了,那这个时候呢我们就需要修改判断矩阵,我们把刚刚那个错误调换过来,其实就是作品数量和作品质量的一个重要程度的一个关系,经计算呢,修改后的判断矩阵CR是0.04,小于0.1,他就通过了一致性检验,通过一致性检验呢就可以求权重了

4、求权重
(1)算术平均法
求权重一共有三种方法,分别是算术平均法,几何平均法以及特征值法,首先呢我们来看一下算术平均法怎么求权重,第一步是把判断矩阵按照列进行归一化,第二步将归一化的各类相加,那就是按行进行求和,第三步是把相加后的向量,每个元素除以N,它就是得到的权重向量了。

(2)几何平均法
第二个我们来看几何平均法求权重啊,几何平均法是把判断矩阵按照行相乘,得到一个新的列向量,然后将新的向量的每个分开N次方,然后对该向量的进行归一化就可以得到权重向量。

(3)特征值法
我们可以仿照一致矩阵求权重的求法,因为这个时候我们判断矩阵一致性是可以接受的,所以就可以仿照这种求法,首先呢我们求出矩阵A的最大特征值,以及特征向量,然后我们再对特征向量进行归一化,就可以得到我们的权重。

(4)求评分

四、相关代码
1、Matlab相关代码
(1)一致性检验代码
%代码一致性检验
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 1/2;1/5 1/2 2 1];
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1];
A = input('判断矩阵A='); %输入判断矩阵
[n,n] = size(A); %获取A的行和列
%求出最大特征值以及对应的特征向量
[V,D] = eig(A); %V是特征向量 D是特征值构成的对角矩阵
Max_eig = max(max(D)); %先求出每一列的最大值,再求最大值中的最大值
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
%注意哦,这里的RI最多支持 n = 15
%这里n=2时,一定是一致矩阵,所以CI = 0,我们为了避免分母为0,将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR<0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end(2)求权重代码
1)算术平均法求权重
%1.算术平均法计算权重
%输入样例:
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1];
A = input('判断矩阵A='); %输入判断矩阵
ASum = sum(A,1); %将判断矩阵每列求和
[n,n] = size(A); %获取A的行和列,用于对ASum复制,对应位相除归一化
Ar = repmat(ASum,n,1); %复制Asum n行1列为Ar矩阵
Stand_A = A./Ar; %归一化
ASumr = sum(Stand_A,2); %各列相加到同一行
disp(ASumr/n); %将相加后得到的向量每个元素除以n可以得到权重向量2)几何平均法求权重
%2.几何平均法计算权重
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1];
clc;
A = input('判断矩阵A='); %输入判断矩阵
[n,n] = size(A); %获取A的行和列
prod_A = prod(A,2); %将A中每一行元素相乘得到一列向量
prod_n_A = prod_A.^(1/n); %将新的向量的每个分量开n次方等价求1/n次方
re_prod_A = prod_n_A./sum(prod_n_A);%归一化处理
disp(re_prod_A); %展示权重结果3)特征值法求权重
%3.特征值法计算权重
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1];
clc;
A = input('判断矩阵A='); %输入判断矩阵
[n,n] = size(A); %获取A的行和列
%求出最大特征值以及对应的特征向量
[V,D] = eig(A); %V是特征向量 D是特征值构成的对角矩阵
Max_eig = max(max(D)); %先求出每一列的最大值,再求最大值中的最大值
[r,c] = find(Max_eig == D,1);%使用find()函数找出最大特征值对应的特征向量
%对特征向量进行归一化得到所需权重
disp(V(:,c)./sum(V(:,c)));2、Python相关代码
(1)一致性检验代码
import numpy as np
# 定义矩阵A
# A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2], [1/3, 2, 1, 1/2], [1/5, 1/2, 2, 1]])
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2], [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
n = A.shape[0] # 获取A的行
# 求出最大特征值以及对应的特征向量
eig_val, eig_vec = np.linalg.eig(A) # eig_val是特征值, eig_vec是特征向量
Max_eig = max(eig_val) # 求特征值的最大值
CI = (Max_eig - n) / (n-1)
RI = [0, 0.0001, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59]
# 注意哦,这里的RI最多支持 n = 15
# 这里n=2时,一定是一致矩阵,所以CI = 0,我们为了避免分母为0,将这里的第二个元素改为了很接近0的正数
CR = CI / RI[n]
print('一致性指标CI=', CI)
print('一致性比例CR=', CR)
if CR < 0.10:
print('因为CR<0.10,所以该判断矩阵A的一致性可以接受!')
else:
print('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!')
(2)求权重代码
1)算术平均法求权重
import numpy as np
# 定义判断矩阵A
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2], [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
# 计算每列的和
ASum = np.sum(A, axis=0)
# 获取A的行和列
n, _ = A.shape
# 归一化
Stand_A = A / ASum
# 各列相加到同一行
ASumr = np.sum(Stand_A, axis=1)
# 计算权重向量
weights = ASumr / n
print(weights)
2)几何平均法求权重
import numpy as np
# 定义判断矩阵A
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2], [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
# 获取A的行和列
n, _ = A.shape
# 将A中每一行元素相乘得到一列向量
prod_A = np.prod(A, axis=1)
# 将新的向量的每个分量开n次方等价求1/n次方
prod_n_A = np.power(prod_A, 1/n)
# 归一化处理
re_prod_A = prod_n_A / np.sum(prod_n_A)
# 展示权重结果
print(re_prod_A)
3)特征值法求权重
import numpy as np
# 定义判断矩阵A
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2], [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
# 获取A的行和列
n, _ = A.shape
# 求出特征值和特征向量
eig_values, eig_vectors = np.linalg.eig(A)
# 找出最大特征值的索引
max_index = np.argmax(eig_values)
# 找出对应的特征向量
max_vector = eig_vectors[:, max_index]
# 对特征向量进行归一化处理,得到权重
weights = max_vector / np.sum(max_vector)
# 输出权重
print(weights)文章来源地址https://www.toymoban.com/news/detail-823076.html
文章来源:https://www.toymoban.com/news/detail-823076.html
到了这里,关于【数学建模美赛 | 国赛必学模型算法精讲】层次分析法——模型原理及Matlab+Python双语言代码演示的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!