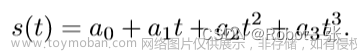👨🏫🥰🥳需要机械臂相关资源的同学可以在评论区中留言哦🤖😽🦄
指南目录📖:
🎉🎉机械臂速成小指南(零点五):机械臂相关资源🎉🎉
机械臂速成小指南(零):指南主要内容及分析方法
机械臂速成小指南(一):机械臂发展概况
机械臂速成小指南(二):机械臂的应用
机械臂速成小指南(三):机械臂的机械结构
机械臂速成小指南(四):机械臂关键部件之减速机
机械臂速成小指南(五):末端执行器
机械臂速成小指南(六):步进电机驱动器
机械臂速成小指南(七):机械臂位姿的描述方法
机械臂速成小指南(八):运动学建模(标准DH法)
机械臂速成小指南(九):正运动学分析
机械臂速成小指南(十):可达工作空间
机械臂速成小指南(十一):坐标系的标准命名
机械臂速成小指南(十二):逆运动学分析
机械臂速成小指南(十三):轨迹规划概述
机械臂速成小指南(十四):多项式插值轨迹规划
机械臂速成小指南(十五):线性规划
机械臂速成小指南(十六):带抛物线过渡的线性规划
机械臂速成小指南(十七):直线规划
机械臂速成小指南(十八):圆弧规划
机械臂速成小指南(十九):机械臂的电路板抓取实验
机械臂速成小指南(二十):机械臂的位姿重复性实验
机械臂速成小指南(二十一):几何雅可比矩阵
机械臂速成小指南(二十二):机械臂逆运动学的数值解方法
机械臂速成小指南(二十三):Paul方法求解机械臂运动学逆解(含matlab代码)
🦾🌏🪐以下为正文🦾🌏🪐
多项式插值(polynomial interopolation)在工业中的应用十分常见,常用的几种多项式插值法有:直接法、拉格朗日插值法和牛顿插值法。多项式插值轨迹规划也是一种常用的关节空间轨迹规划方法。
下面,我们将以机械臂作点对点运动为例,从理论分析、程序仿真及实际应用三个方面对多项式插值轨迹规划进行介绍。
一、三次多项式(cubic polynomial)插值轨迹规划
1.理论分析
点对点运动的过程中,机械臂必须在规定的时间t_f内到达目标点,各个关节也从初始状态转变为期望状态。
机械臂初始位姿与期望位姿均已知,那么我们通过逆运动学运算就可以得到这两个状态下的关节变量。
设初始时刻为t_0,则我们需要将每一个关节在(t_0,t_f)时间内的角度变化与时间的关系使用三次多项式进行描述,该多项式称为关节角度函数。以关节1为例,初始角度为θ_0,期望角度为θ_f。那么,关节1的关节角度函数曲线一定通过(t_0,t_0)与点(t_f,t_f)。

为了确定该三次多项式的4个系数,我们必须找到4个约束条件。我们已经知道了初始时刻与终止时刻机械臂的状态,这就可以确定2个约束条件,即

此时,还缺少2个约束条件。由于机械臂进行的是点对点运动,机械臂的各关节角速度在t_0 与t_f 时刻均为0,可表示为

该三次多项式可表示为

则关节角速度与关节角加速度可分别表示为上述三次多项式的一次导数与二次导数,即

将4个约束条件与上式联立即可得到三次多项式的4个系数,即

2.程序仿真
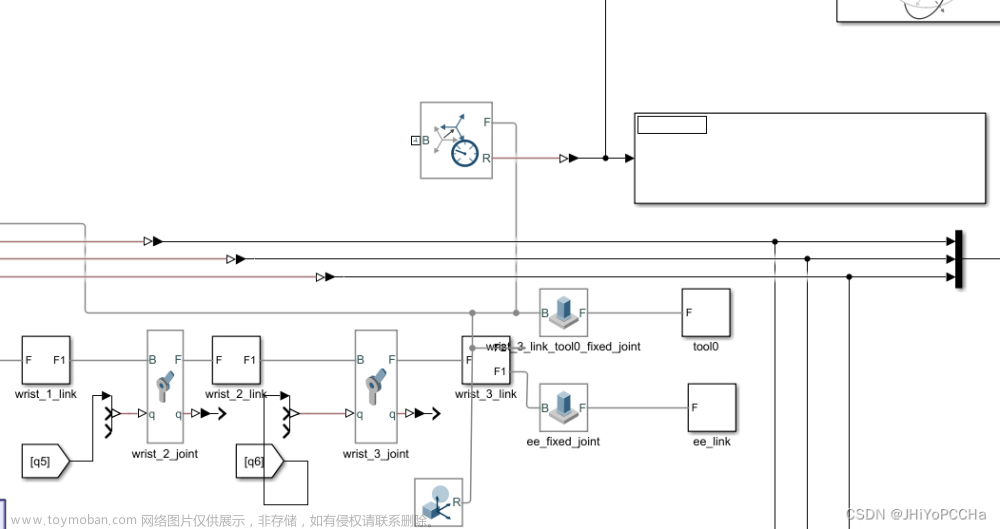
使用MATLAB中的RTB工具箱对该轨迹规划方法进行仿真:
首先,定义3个数组用于储存机械臂关节的角度、角速度及角加速度,用于绘制图像。
q = zeros(step,N); %初始化机械臂关节的角度
qd = zeros(step,N); %初始化机械臂关节的角速度
qdd = zeros(step,N); %初始化机械臂关节的角加速度
第二步,按照上一小节中的计算思路计算多项式的4个系数。
a_0 = init_ang; %三次多项式的第1个系数
a_1 = zeros(1,6); %三次多项式的第2个系数
a_2 = 3/(step^2)*(targ_ang-init_ang); %三次多项式的第3个系数
a_3 = -2/(step^3)*(targ_ang-init_ang); %三次多项式的第4个系数第三步,计算正运动学方程、输出末端轨迹并进行动画演示。

T=robot.fkine(q); %运动学正解
nT=T.T; %转为齐次变换矩阵
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:))); %输出末端轨迹
title('三次多项式插值轨迹');
robot.plot(q); %动画演示最后一步,将关节的角度曲线、角速度曲线以及角加速度曲线绘制出来。

figure(f)
subplot(6, 1, 1);
plot(q(:,1));
title('关节1角度(三次多项式插值)');机械臂轨迹规划之三次多项式插值规划matlab仿真程序https://download.csdn.net/download/m0_53966219/87521943?spm=1001.2014.3001.5503
3.编程实现
与仿真不同的一点是,在对机械臂进行实际控制时,是要考虑到轨迹点生成个数对于轨迹精度的影响的。因为关节变量与时间的函数是连续的,但我们所发送给上位机的指令实际上是一个个离散的轨迹点对应的关节变量。生成的轨迹点太多,运算量会增加;生成的轨迹点太少,机械臂的运行轨迹就会不够平滑。
本文使用python编写上位机完成轨迹规划中的运算。
首先,需要检测轨迹规划运算结果是否在机械臂的可达工作空间以及关节限度之内。
if (J1newAng < J1NegAngLim or J1newAng > J1PosAngLim) or (J2newAng < J2NegAngLim or J2newAng > J2PosAngLim) or (J3newAng < J3NegAngLim or J3newAng > J3PosAngLim) or (J4newAng < J4NegAngLim or J4newAng > J4PosAngLim) or (J5newAng < J5NegAngLim or J5newAng > J5PosAngLim) or (J6newAng < J6NegAngLim or J6newAng > J6PosAngLim or TrackNew < 0 or TrackNew > TrackLength):
almStatusLab.config(text="AXIS LIMIT", bg = "red")
almStatusLab2.config(text="AXIS LIMIT", bg = "red")
tab1.runTrue = 0其次,对于每一个关节进行运算,以关节1为例:
J1calcAng = float(J1newAng) - float(J1AngCur)
J1steps = int(J1calcAng / J1DegPerStep)
J1StepCur = J1StepCur + J1steps #Invert
J1AngCur = round(J1NegAngLim + (J1StepCur * J1DegPerStep),2) #四舍五入,小数点为2
J1steps = str(J1steps)最后,生成指令字符串。
J1curAngEntryField.delete(0, 'end')
J1curAngEntryField.insert(0,str(J1AngCur))
二、五次多项式(quintic polynomial)插值轨迹规划
1.理论分析
当我们使用五次多项式对关节空间轨迹进行插值时,需要求解对应的6个系数,即与上文相比,我们需要再设定2个约束条件。
为保证关节速度函数的连续,假设在t_0 与t_f 时刻,机械臂的各关节角加速度为0,即

此时我们可以唯一确定一个五次多项式,同样令t_0=0 ,该多项式可表示为

将6个约束条件与上式联立,可得到五次多项式的系数为

2.程序仿真
我们使用MATLAB的RTB工具箱中自带函数jtraj()完成五次多项式轨迹规划的仿真:
[qt,qdt,qddt] = jtraj(q0, q1, tv, qd0, qd1)
其中,qt、qdt、qddt分别为关节的旋转角度、角速度以及角加速度;q0、q1分别为关节的初始角度与终止角度;tv为生成的轨迹点个数;qd0与qd1分别为机械臂在起始点处及终止点处的速度,默认为0。
关键代码段如下所示。
%轨迹规划
f = 1;
figure(f)
step = 50;
[q ,qd, qdd]=jtraj(init_ang,targ_ang,step); %五次多项式轨迹,得到关节角度,角速度,角加速度,50为采样点个数
grid on
T=robot.fkine(q); %根据插值,得到末端执行器位姿
nT=T.T;
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹其余代码与三次多项式轨迹规划仿真一致。文章来源:https://www.toymoban.com/news/detail-823356.html
机械臂轨迹规划之五次多项式插值规划matlab仿真代码https://download.csdn.net/download/m0_53966219/87521950?spm=1001.2014.3001.5503文章来源地址https://www.toymoban.com/news/detail-823356.html
到了这里,关于机械臂速成小指南(十四):多项式插值轨迹规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!