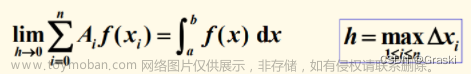线性方程组的理论求解公式——,在实际应用中面临着两大问题,1是计算过程复杂,2是无法保证算法的稳定性。同时初始数据存在误差,需要寻求能达到精度要求的、操作和计算过程相对简单的求解方法——迭代法。
目录
一.迭代法的基本思想
二.基本迭代法
2.1雅可比迭代
2.1.1三阶线性方程组的雅可比(Jacobi)迭代法
2.1.2雅可比迭代法的矩阵描述
2.2高斯-赛德尔迭代法
2.2.1三阶线性方程组的高斯-赛德尔迭代法
2.2.2高斯-赛德尔迭代法的矩阵描述
三.迭代法的收敛性
3.1迭代法的收敛性判别
3.1.1迭代矩阵的范数编辑
3.1.2迭代矩阵的谱半径
3.2收敛性的性质
四.参考资料
一.迭代法的基本思想
基本思想是在逐步逼近方程组的精确解的迭代过程中获得满足精度要求的近似解。为了避免困难的矩阵求逆运算,将方程组写成等价形式。 等价格式如下:

迭代格式如下:

对于给定的线性方程组,可以写成不同的(无穷多)迭代格式,有意义的(可用的)迭代格式应具有收敛性——生成的解向量序列收敛于方程组的解;而好的迭代法应具有较高的收敛速度。接下来介绍几种常见的迭代法。
二.基本迭代法
2.1雅可比迭代
2.1.1三阶线性方程组的雅可比(Jacobi)迭代法
例题:
解下列方程组,精确解x*=。

(1)将三阶线性方程组写成等价形式:

(2)构造迭代公式,即雅可比迭代公式:

(3)取初始向量,即。代入迭代公式,求出:

(4)作为初始向量继续代入迭代公式进行迭代,求出。
(5)不断迭代下去,从表中看出迭代解不断接近精确解.

2.1.2雅可比迭代法的矩阵描述
雅可比迭代公式的矩阵形式为 ,其中B是迭代矩阵。 将方程组的系数矩阵A,分成A=D-L-U,具体如下:

则方程组可以写成这种形式

2.2高斯-赛德尔迭代法
2.2.1三阶线性方程组的高斯-赛德尔迭代法
例题:
解下列方程组,精确解x*=。

(1)将三阶线性方程组写成等价形式:

(2)构造迭代公式,即高斯-赛德尔迭代公式:

(3)取初始向量,即代入迭代公式,迭代得到的新,替代初始,代入迭代中,求出:

(4)作为初始向量继续代入迭代公式进行迭代,迭代得到的新,替代初始,代入迭代中——求出。
(5)不断迭代下去, 从表中看出迭代解不断接近精确解.

2.2.2高斯-赛德尔迭代法的矩阵描述
高斯-赛德尔迭代公式的矩阵形式为 。其中B是迭代矩阵。 同样分解A为A=D-L-U。 则方程组可以写成这种形式:

进一步写成迭代形式:

展开为:

三.迭代法的收敛性
3.1迭代法的收敛性判别
3.1.1迭代矩阵的范数
迭代矩阵的范数是迭代法收敛的充分条件,迭代矩阵的范数小于1是迭代法收敛的充分条件,
3.1.2迭代矩阵的谱半径
迭代法收敛的基本定理,迭代公式收敛的充要条件是迭代矩阵B的谱半径小于1。
例题:
对于下面方程组,证明:雅可比迭代法收敛而高斯-赛德尔迭代法发散。

证明 1) 对于雅可比迭代矩阵

的特征方程为

解得,为的特征根,显然,因此雅可比迭代收敛。
证明 2) 对于高斯-赛德尔迭代矩阵
其迭代矩阵为

的特征方程为

解得,因此高斯-赛德尔迭代法发散。
3.2收敛性的性质
对于一个线性方程组Ax=b,不同性质的A导致两种迭代法有不同的收敛。
(1)若A为严格对角占优矩阵,则解Ax = b的雅可比迭代过程和高斯-赛德尔迭代过程均收敛。 (2)若A是对称正定方阵,则解Ax=b的高斯-赛德尔迭代过程收敛。
四.参考资料
1.<<数值分析>>北京理工大学出版,感谢曾繁慧 胡行华两位老师。文章来源:https://www.toymoban.com/news/detail-823915.html
2.辽宁工程技术大学,工程数学考试参考。 文章来源地址https://www.toymoban.com/news/detail-823915.html
到了这里,关于<<数值分析>> 第三章线性方程组的迭代解法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!