理顺 QR 分解算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了理顺 QR 分解算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

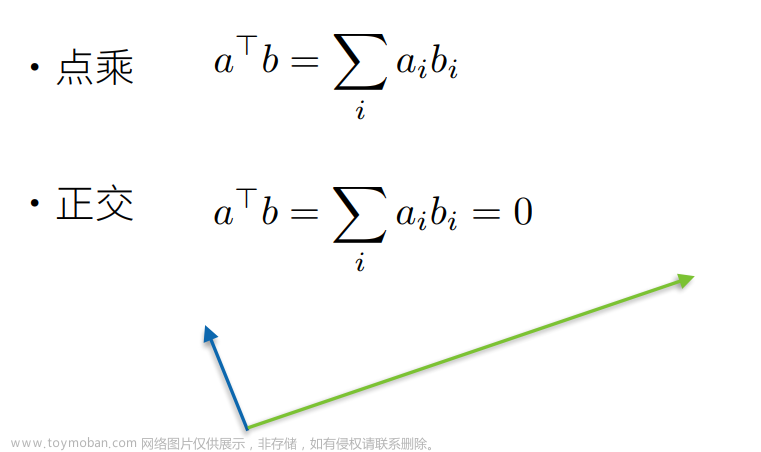
咱们网站的这个公式编辑器，估计是后台生成图片后贴回来的，固定分辨率而且分辨率不高。

还不如先离线 latex 生成 pdf 后再截图上来

1. Why QR

When A and b are known, to solver the minimization of , where .

The reduction of A to various canonical form via orthogonal transformations should use Householder reflections and Givens rotations.

2. preview on orthogonal matrix

2.1 Orthogonal matrix

is orthogonal matrix, if:

2.2 rotation matrix is orthogonal matrix

is orthogonal and is a rotation matrix.

If , then is obtained by rotating counterclockwise through an angle .

2.3 reflection matrix is orthogonal matrix

is orthogonal and is a reflection matrix.

If , then is obtained by reflecting the vector across the line defined by

That means and are axial symmetry by S,

x is the preimage, y is the image, S is the mirror surface.

looks like :

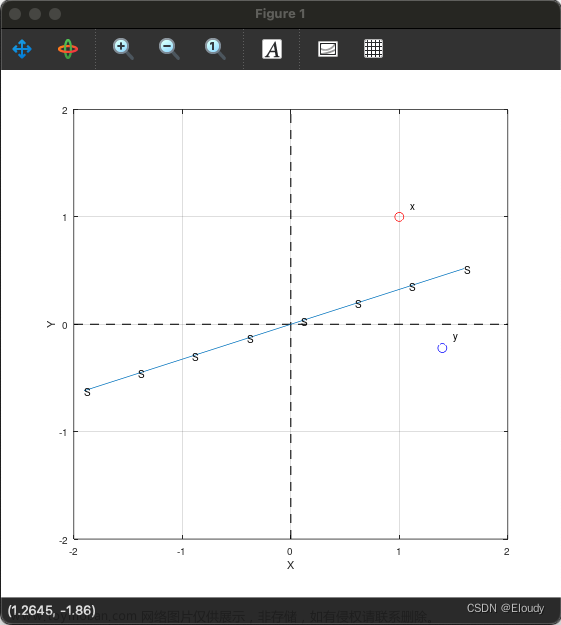
理顺 QR 分解算法,线性代数,算法,矩阵计算

%input x, ta = theta

%x = [-sqrt(2)/2.0, sqrt(2)/2.0]
x = [1; 1;]
ta = pi/5

S = [cos(ta/2.0), sin(ta/2.0)]
Q = [cos(ta), sin(ta); sin(ta), -cos(ta);]

y = Q*x

figure;
%1. draw axis
xmin = -2
xmax = 2
ymin = -2
ymax = 2

axisx = xmin:xmax;
axisy = zeros(size(axisx));
plot(axisx, axisy, 'k--', 'LineWidth', 0.7); % Plot x=0 axis
hold on;
plot(axisy, xmin:xmax, 'k--', 'LineWidth', 0.7); % Plot y=0 axis
hold on;

%2. draw surface of mirror
sx = -2*S(1):0.5:2*S(1)
sy = (S(2)/S(1))*sx
plot(sx, sy)
text(sx,sy, 'S')
hold on;

%3. draw preimage
plot(x(1), x(2), 'ro')

text(x(1)+0.1, x(2)+0.1, 'x')
hold on;

%4. draw image
plot(y(1), y(2), 'bo')
text(y(1)+0.1, y(2)+0.1, 'y')

%5. axis label
xlabel("X")
ylabel('Y')
v=[xmin, xmax, ymin, ymax]
axis(v)
%axis on

3. Householder transformation

3.1 Householder matrix

In section 2, the reflection is introduced from the mirror surface. But, in this section, it is introduced from normal direction.

Let

then is

which are synonyms.

And is the .

When

is the image from by reflecting with the hyuperplane and the mirror surface is cross the point.

let (this is the normal direction)

then ;

约化定理：

Let ,

then st.

and:

$理顺 QR 分解算法,线性代数,算法,矩阵计算$ (1)

约化定理毕；

约化定理example：

Let then , and

to calculate :

then

$理顺 QR 分解算法,线性代数,算法,矩阵计算$

Here is the matlab code:

reduce_01.m:

x=[3;5;1;1;]
sigmaa =sign(x(1))*norm(x)
u = x+sigmaa*eye(4)(:,1)
betaa = 0.5*(norm(u))^2
H = eye(4) - (1.0/betaa)*u*u'
%debug
%h=betaa*H

y = H*x

理顺 QR 分解算法,线性代数,算法,矩阵计算

3.2 QR decompose

Theorems 3:

and then is orthogonal matrix, st. , and is a upper triangular matrix.

Theorems 4:

and then and , is orthogonal matrix, and is a upper triangular matrix, st. .

and if , then the decomposition is unique.

Let‘s more concrete, do an example:

Ex3,

decompose , with

PF:

1-st column:

By formulas (1), calculate st.

$理顺 QR 分解算法,线性代数,算法,矩阵计算$

matlab codes:

A=[
 2,-2, 3;
 1, 1, 1;
 1, 3,-1;
]
x=A(:,1)
sigma=sign(x(1))*sqrt(x'*x)
miu=x+sigma*eye(3)(:,1)
beta=sigma*(sigma + x(1))
H=eye(3) -(1.0/beta)*miu*miu'
H*A

理顺 QR 分解算法,线性代数,算法,矩阵计算

2nd-column:

find , st.

with the formulas again:

$理顺 QR 分解算法,线性代数,算法,矩阵计算$

now

$理顺 QR 分解算法,线性代数,算法,矩阵计算$

for ,let

and

matlab codes：

A=[
 2,-2, 3;
 1, 1, 1;
 1, 3,-1;
]
x=A(:,1)
sigma=sign(x(1))*sqrt(x'*x)
miu=x+sigma*eye(3)(:,1)
beta=sigma*(sigma + x(1))
H1=eye(3) -(1.0/beta)*miu*miu'


A1=H1*A
x = A1(2:3,2)
sigma = sign(x(1))*sqrt(x'*x)
miu = x+sigma*eye(2)(:,1)
beta=sigma*(sigma+x(1))	
H2_=eye(2) - (1.0/beta)*miu*miu'

H2=zeros(3,3)
H2(2:3,2:3)=H2_
H2(1,1) = 1

A2 = H2*A1
R=-eye(3)*A2

Q=(-eye(3)*H2*H1)'

理顺 QR 分解算法,线性代数,算法,矩阵计算