目录
一、插入排序的相关概念
1、基本思想
2、基本操作:有序插入
二、插入排序的种类
三、直接插入排序
1、直接插入排序的过程:顺序查找法查找插入位置
2、使用“哨兵”直接插入排序
四、 直接插入排序算法描述
五、折半插入排序
1、查找插入位置时采用折半查找法,如下图所示:
2、折半插入排序——算法描述
3、折半插入排序——算法分析
六、希尔排序
1、基本思想:
2、希尔排序算法的特点:
3、希尔排序的典例
4、由上图可知,希尔排序的思路
5、希尔排序的特点
6、希尔排序的算法描述
一、插入排序的相关概念
1、基本思想
每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。即边插入边排序, 保证子序列中随时都是排好序的。就像玩扑克牌抓牌的时候。
2、基本操作:有序插入
■在有序序列中插入一个元素,保持序列有序,有序长度不断增加。
■起初,a[0]是长度为1的子序列。然后,逐一将a[1]至a[n-1 ]插入到有序子序列中。
二、插入排序的种类
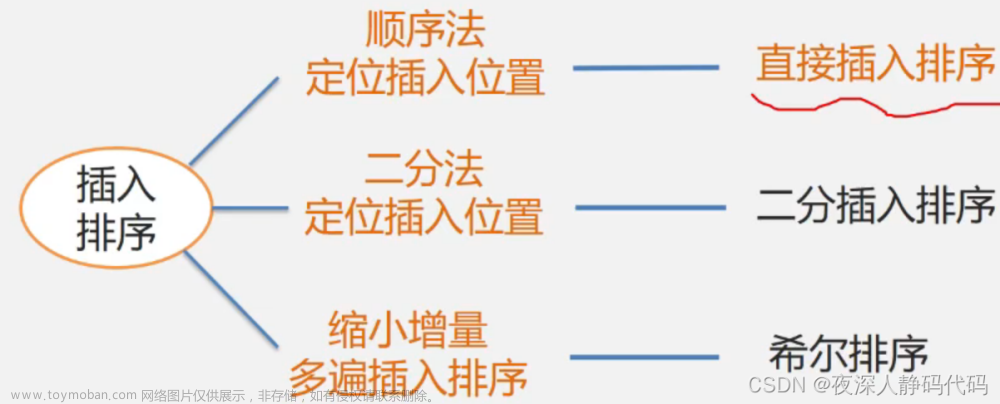
三、直接插入排序
1、直接插入排序的过程:顺序查找法查找插入位置

(1)直接插入排序在基本有序时,效率较高。
(2)在待排序的记录个数较少时,效率较高。
2、使用“哨兵”直接插入排序

四、 直接插入排序算法描述
void InsertSort(SqList &L){
int i, j;
for (i=2; i<=L.length; ++i) {
if (L.r[i].key < L.r[i-1].key){ //若"<"需将L.r[i]插入有序子表
L.r[0]=L.r[i]; //复制为哨兵
for (j=i-1;L.r[O].key<L.r[j].key; --j){
L.r[j+1]=L.r[j]; //记录后移
}
L.r[j+1]=L.r[O]; //插入到正确位置
}
}五、折半插入排序
1、查找插入位置时采用折半查找法,如下图所示:
2、折半插入排序——算法描述
void BInsertSort (SqList &L){
for(i= 2; i <= L.length; ++i){ //依次插入第2~第n个元素
L.r[0] = L.r[i]; //当前插入元素存到"哨兵"位置
low= 1;high= i-1; //采用二分查找法查找插入位置
while (low <= high) {
mid= (low+high)/2;
if ( L.r[O].key < L.r[mid].key ) high = mid -1;
else low=mid+1;
} //循环结束,high+1则为插入位置
for (j=i-1;j>=high+1;--j)
L.r[j+1]= L.r[j; //移动元素
L.r[high+1] = L.r[0]; //插入到正确位置
}
} //BInsertSort3、折半插入排序——算法分析
(1)折半查找比顺序查找快,所以折半插入排序就平均性能来说比直接插入排序要快;
(2)它所需要的关键码比较次数与待排序对象序列的初始排列无关,仅依赖于对象个数。
(3)当n较大时,总关键码比较次数比直接插入排序的最坏情况要好得多,但比其最好情况要差;
(4)在对象的初始排列已经按关键码排好序或接近有序时,直接插入排序比折半插入排序执行的关键码比较次数要少;
(5)折半插入排序的对象移动次数与直接插入排序相同,依赖于对象的初始排列
减少了比较次数,但没有减少移动次数
六、希尔排序
1、基本思想:
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
2、希尔排序算法的特点:
(1)缩小增量
(2)多遍插入排序
3、希尔排序的典例

4、由上图可知,希尔排序的思路
①定义增量序列: >>...>=1;
上图的典例就是:D3=5;D2=3;D1=1;
②对每一个进行“-间隔”插入排序(k=M,M-1,...1)文章来源:https://www.toymoban.com/news/detail-824479.html
5、希尔排序的特点
一次移动,移动位置较大,跳跃式地接近排序后的最终位置,最后一次只需要少量移动。文章来源地址https://www.toymoban.com/news/detail-824479.html
6、希尔排序的算法描述
void ShellSort (Sqlist &L int dlta[], int t){ //按增量序列dlta[0...t- 1]对顺序表L作希尔排序。
for(k=O; k<t; ++k)
Shellinsert(L, dlta[k]); //一趟增量为dlta[k]的插入排序
}//ShellSort
void ShellInsert(SqList &L,int dk)
//对顺序表L进行一趟增量为dk的Shell排序,dk为步长因子
for(i=dk+1; i<=L.length; ++i)
if(r[i].key < r[i-dk].key) {
r[0]=r[i];
for(j=i-dk; j>0 &&(r[0].key<r[j].key); j=j-dk)
r[j+dk]=r[j];
r[j+dk]=r[0];
}
}到了这里,关于插入排序超详解释,一看就懂的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!