MPC(模型预测控制)-Simulink仿真-Toy模板网

这篇具有很好参考价值的文章主要介绍了MPC(模型预测控制)-Simulink仿真。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、为什么使用MPC控制器?

① MPC可以处理多输入耦合控制多输出的问题:
② MPC可以处理对于控制量有约束的问题

比如，驾驶汽车的时候，汽车速度和转角都有上限
③ MPC具有预测效果

即MPC考虑的不是根据当前参考值进行控制，而是根据预测时间内的参考去预测当前的控制量，比如在小车转弯时，就避免了可能在过弯处急转弯。

mpc控制,算法,matlab,自动驾驶

MPC需要的算力高一些，因为MPC控制过程中，每个时间步都要求解一个相同形式不同参数的优化问题。

二、什么是MPC控制器?

mpc控制,算法,matlab,自动驾驶

小车的数学模型:

mpc控制,算法,matlab,自动驾驶

item	inputs	outputs
Plant Model(被控对象的数学模型)	之后m个控制量	之后p个时间步的预测输出

优化器：

mpc控制,算法,matlab,自动驾驶

item	inputs	outputs
优化器	(数学模型, 之后p个时间步的参考轨迹, 约束条件)	之后m个控制量

优化器要考虑两点:

① 预测轨迹与参考轨迹偏差最小

②控制量不突变
$\doteq J = \sum_{i=1}^{p} w_e e_{k+i}^2 + \sum_{i=0}^{p-1} w_{\Delta u} {\Delta u_{k+i}}^2$

${\color{Red} 尽管优化器输出的是之后p个时间步的控制量，但是在当前时间步，}\\ {\color{Red} MPC仅将这个最有序列的第一步应用到汽车上，忽略其余部分}$

三、MPC控制器的参数如何设置?

参数既会影响控制器的性能，又会影响计算复杂度。
MPC主要的参数如下:
- ① 采样时间
- ② 预测范围、控制范围
- ③ 约束
- ④ 损失函数的权重

3.1 采样时间

采样时间过大，当干扰发生，控制器无法做出及时的反应。

采样时间过小，会导致过多的计算负载。

mpc控制,算法,matlab,自动驾驶

可以测量系统的阶跃响应，根据上升时间选择采样时间

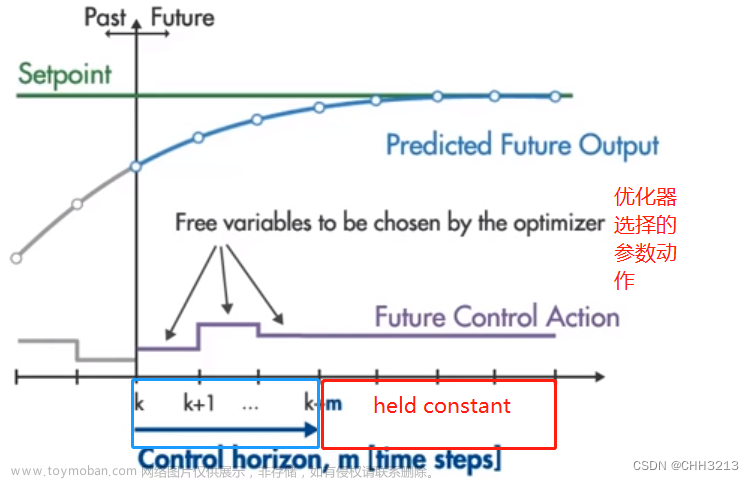
3.2 预测范围、控制范围

我们应该选择一个涵盖系统重要动态的预测范围

预测范围过短，无法及时反映，可能会在弯道处急转弯

预测范围过长，之后的不可预测事件可能会白白浪费算力。

我们通常选择 20-30个样本覆盖系统的动态响应，如下图:

mpc控制,算法,matlab,自动驾驶

通常只有前几个时间步的控制对于预测影响较大(因为前几个要拽向ref轨迹，后面的维持稳定)，因此，选择大的控制范围只会白白增大计算复杂度

经验法则: 控制范围 = 10%~20% × 预测范围

3.3 约束条件

可以对控制量、控制量变化率、状态量进行约束

约束分为硬约束和软约束，无法违反的(比如最大车速)叫硬约束

软约束可以违反，但我们不希望违反，可以把它设计到损失函数之中

建议将输出约束设置为软约束，并避免对控制量及其变化率设置硬约束，否则可能会出现无解的情况

3.4 权重

损失函数由多个部分组成，需要设置权重

比如最基本的，我们既希望预测轨迹接近参考轨迹，又希望控制量是平滑的。

四、自适应增益调度和非线性MPC

mpc控制,算法,matlab,自动驾驶

线性系统 + 线性约束 + 时不变约束条件 => 可以使用线性时不变MPC控制器 => 凸优化问题

mpc控制,算法,matlab,自动驾驶

但是如果系统是非线性的，就要使用自适应MPC、时间表MPC
- 自适应MPC：具体思路是在非线性模型的各个工作点，建立多套线性模型
  
  自适应MPC的线性模型在不同工作点上结构，超参数相同，只是矩阵参数不同而已

mpc控制,算法,matlab,自动驾驶

时间表MPC: 对于不同工作点，需要设置不同数量超参数(控制量数目、预测步长…)的模型

如果是非线性的，那么优化问题就会变成多极值点的非凸优化问题，求解较复杂

mpc控制,算法,matlab,自动驾驶

五、Simulink仿真MPC控制器

mpc控制,算法,matlab,自动驾驶

item	value
输出量(状态量)	(横向位置Y、偏航角\phi)
控制量	(前轮转角delta)

$假定V_x恒为15m/s , 使用线性化汽车模型\\$

模型下载地址: https://www.mathworks.com/matlabcentral/fileexchange/68992-designing-an-mpc-controller-with-simulink?s_eid=PSM_15028

(一定要记得路径，matlab界面的路径一定得是模型文件路径。路径不对的话，plant和reference的mask无法显示正确，会显示问号，同时直接运行会报错)

步骤: https://ww2.mathworks.cn/help/releases/R2017b/mpc/examples/autonomous-vehicle-steering-using-model-predictive-control.html

5.1 数学分析

下面依次介绍各个模块:

① Plant: 车辆线性模型

右键Plant模块，选择Block Parameters：

mpc控制,算法,matlab,自动驾驶

变量	含义
$V_x$	小车平行于车身向前的速度
$m$	小车总质量
$I_z$	Yaw夹角转动惯量(绕小车中心旋转的转动惯量)
$l_f$	小车质心到前轮的距离
$l_r$	小车质心到前轮的距离
$C_{\alpha}$	汽车转角刚度((轮胎侧偏角的单位增量所对应的横向力的增量) (N/rad)
$\psi$	Yaw角

${\color{Red} 小车是自行车模型(bicycle \quad model\quad with \quad two\quad degrees\quad of \quad freedom), 且V_x恒为15m/s:}$

reference: 小车的自行车模型

mpc控制,算法,matlab,自动驾驶

原理(1): 前轮运动 = 前轮相对于车身运动 + 车身相对于质心运动(旋转) + 小车质心相对于地面运动
原理(2): $\Delta 轮胎受到垂直于车身的力 = C_{r}(或者C_{l} ) \Delta 轮胎转角$

(注意: 自行车模型代替小车模型时，四轮变为两轮，因此 $自行车的C_f应该是小车的2C_f$ )

进行动力学分析：
$由于\psi较小，简化为线性模型即: \dot{Y} = V_x \psi + V_y \quad [公式一]\\$
$\Delta 前轮相对于车身转角 = (\frac{V_y + \dot{\psi}l_f}{V_x}) \\ \Delta 后轮相对于车身转角 = (- \frac{V_y - \dot{\psi}l_r}{V_x}) \\ \Rightarrow \\ 前轮受到垂直于车身的力 = 2C_{f} (-\psi + \delta + \Delta 前轮相对于车身转角) \\ 后轮受到垂直于车身的力 = 2C_{r} (-\psi + \Delta 后轮相对于车身转角)\\ \Rightarrow \\ 根据[公式一]: \\ m \ddot{y} = -mV_x \dot{\psi} - m\dot{V_y}\\ m\dot{V_y}=前轮受到垂直于车身的力 + 后轮受到垂直于车身的力 \\ \Rightarrow m\ddot{y} = - m V_x \dot{\psi} + 2C_f[-\psi +\delta - \frac{V_y + \dot{\psi}l_f}{V_x}] +2 C_r (-\psi - \frac{V_y - \dot{\psi}l_r}{V_x}) \\ 将 [公式一]代入到上式: \\ {\color{Red}\ddot{y} = -\frac{2C_f+2C_r}{mV_x}\dot{y} -(V_x+\frac{2C_fl_f-2C_rl_r}{mV_x}) \dot{\psi} + \frac{2C_{\alpha} \delta}{m} \quad [公式二] }$

$\qquad \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\ \frac{d}{dt} \begin{bmatrix} \dot{y} \\ \psi \\ \dot{\psi} \end{bmatrix} =\begin{bmatrix} -\frac{2C_f+2C_r}{mV_x} & 0 & -(V_x+\frac{2C_fl_f-2C_rl_r}{mV_x}) \\ 0 & 0 & 1\\ -\frac{2l_fC_f-2l_rC_r}{I_z V_x} & 0 & - \frac{2l_f^2C_f+2l_r^2C_r}{I_zV_x} \end{bmatrix} \begin{bmatrix} \dot{y} \\ \psi \\ \dot{\psi} \end{bmatrix} + \begin{bmatrix} 2 \frac{C_f}{m}\\ 0 \\ \frac{2l_fC_f}{I_z} \end{bmatrix} \delta$
正好就是Parameters中的A,B,C,D矩阵