由于考研复试的面试老师可能会问一些数学问题,一位学长也跟我说,研究生要不断地和线性代数和概率论打交道,可能这就是老师喜欢问数学问题的原因吧,这里整理一下。
线性代数知识点:

























合同矩阵:

- 余子式:
n 阶行列式中,划去元 aij所在的第 i 行与第 j 列的元,剩下的元不改变原来的顺序所构成的 n-1 阶行列式称为元aij的余子式。
作用:能把 n 阶的行列式化简为 n-1 阶。
代数余子式是在余子式的前面乘于(-1)^(i+j)系数
- 行列式的含义:
行列式,记作 det(A),是一个将方阵 A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以被认为是衡量矩阵相乘后空间扩大或者缩小了多少。如果行列式是 0, 那么空间至少沿着某一维完全收缩了,使其失去了所有的体积。如果行列式是 1, 那么矩阵相乘没有改变空间体积。
行列式等于它任意一行(列)的各元素与其对应的代数余子式乘积之和。
本质含义(几何意义):行列式就是在给定一组基下,N 个向量张成的一个 N 维广义四边形的体积。2 阶行列式代表的是平面内的面积;3 阶行列式自然而然就是 3 维空间内的体积;4 阶行列式是 4 维空间里的超体积。

- 矩阵的秩和向量组的关系:
矩阵的秩等于它列向量组的秩,也等于它行向量组的秩。
向量组的秩定义为向量组的极大线性无关组所含向量的个数。
- 矩阵的秩和向量空间的关系(几何意义):
任何矩阵的行空间的维数等于矩阵的列空间的维数等于矩阵的秩。
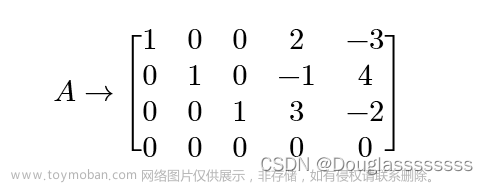
- 矩阵的秩与线性方程组解的关系:
设 A 是 m×n 矩阵,若 R(A)=r<n,则齐次线性方程组 Ax=0 有基础解系,且每个基础解系都含 n-r 个解向量。
-
矩阵的迹:方阵 A(n*n) 的迹定义为对角线元素的和。
-
判断一个线性方程组是否有解有哪几种方法?
- 对于齐次线性方程组 Ax=0
r(A)=n,有惟一零解;r(A)<n,有无穷多解。
- 对于非齐次线性方程组 Ax=b
r(A)≠r(A,b),无解;
r(A)=r(A,b)=n,有唯一解;
r(A)=r(A,b)<n,有无穷多解。
- 描述线性相关与线性无关?略
一个矩阵线性无关的等价定义有什么?
非奇异矩阵、矩阵可逆、矩阵满秩、特征值没有 0。(奇异矩阵:行列式等于零的矩阵(方阵)。)
- 向量空间的基与维数
- 基
设 V 是一向量空间,α1,α2,…,αr∈V且满足:
a)α1,α2,…,αr线性无关;
b) V 中向量均可由α1,α2,…,αr线性表示。
则称α1,α2,…,αr为 V 的一个基。
- 维数
基中所含向量个数 r 称为向量空间的维数。
- 特征值和特征向量
- 定义
对方阵 A 满足:Ax=λx,其中 x 为非零向量,则称 x 为特征向量,λ 为特征值。
- 矩阵的特征值与特征向量有什么关系?
[1] 一个特征值可能对应多个特征向量,一个特征向量只能属于一个特征值。
[2] 属于不同特征值的特征向量一定线性无关。
[3] 设 λ 是 n 阶方阵 A 的一个 k 重特征值(λ 为特征方程的 k 重根),对应于 λ 的线性无关的特征向量的最大个数为l,则 k>=l,即特征值 λ 的代数重数不小于几何重数。
- 特征值和特征向量的意义
如果一个向量投影到一个方阵定义的空间中只发生伸缩变化,而不发生旋转变化,那么该向量就是这个方阵的一个特征向量,伸缩的比例就是特征值。
特征向量的代数含义是:将矩阵乘法转换为数乘操作;特征向量的几何含义是:特征向量通过方阵 A 变换只进行伸缩,而保持特征向量的方向不变。特征值表示的是这个特征到底有多重要,类似于权重,而特征向量在几何上就是一个点,从原点到该点的方向表示向量的方向。
- 正交矩阵?正交向量?
若 (α,β)=0,则称向量 α 与 β 正交。矩阵的转置和矩阵的乘积=单位阵,那么这个矩阵就是正交矩阵,它的列向量组一定是标准正交向量组。正交矩阵的转置等于矩阵的逆的矩阵。
- 合同矩阵:

- 正定矩阵:

前提:矩阵是对称的
正定矩阵的所有特征值大于零
各阶主子式大于零
- 相似与对角化:

相似对角化后,对角线的值就是矩阵 A 的 n 个特征值。


- 施密特变换
求标准正交基的方法。把一个线性无关向量组改造成一个与其等价的正交向量组。

额外文章来源:https://www.toymoban.com/news/detail-825119.html
证明自然对数e为无理数,高数连续性证明,线代海森矩阵,雅克比矩阵,施密特正交,机器学习,矩阵的行秩为啥和列秩相等,正定矩阵七大性质。文章来源地址https://www.toymoban.com/news/detail-825119.html
到了这里,关于考研复试——线性代数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!