-
d3d12龙书阅读----数学基础 向量代数、矩阵代数、变换
- directx 采用左手坐标系
- 点积与叉积
-
点积与叉积的正交化
- 使用点积进行正交化
- 使用叉积进行正交化
- 矩阵与矩阵乘法
- 转置矩阵 单位矩阵 逆矩阵 矩阵行列式
-
变换
- 旋转矩阵
- 坐标变换
-
利用DirectXMath库进行向量运算、矩阵运算以及空间变换
- 头文件与命名空间
- 核心向量类型 XMVECTOR
- FMVECTOR GMVECTOR HMVECTOR CMVECTOR XM_CALLCONV
- XMFLOAT 与 XMVECTOR之间的相互转换
- 向量的初始化
- 向量的运算
- XMMATRIX定义与初始化
- XMMATRIX FXMMATRIX CXMMTRIX
- 矩阵操作的常用函数
- 空间变换
d3d12龙书阅读----数学基础 向量代数、矩阵代数、变换
directx 采用左手坐标系
在directx中,坐标系统一采用左手坐标系,与opengl采用右手坐标系不同
四指向右指向x轴,然后弯曲向y轴,大拇指的方向即z轴正方向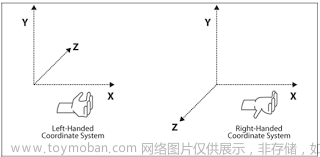
点积与叉积
略
点积与叉积的正交化
规范正交向量集:对于向量集的每个向量,它与其它向量之前都是互相正交,并且都是单位向量
正交化:将不规范正交的集合转换为规范正交的集合
使用点积进行正交化
对于二维 两个向量的正交化来说
将第一个向量作为起始向量,将其标准化为单位向量
然后第二个向量减去在第一个向量上的投影,就只剩下与其正交的那部分,然后再将这部分标准化为单位向量
三维 三个向量
先让v1与v0正交,然后v2减去在v1与v0方向上的投影,再标准化
更一般的结论:

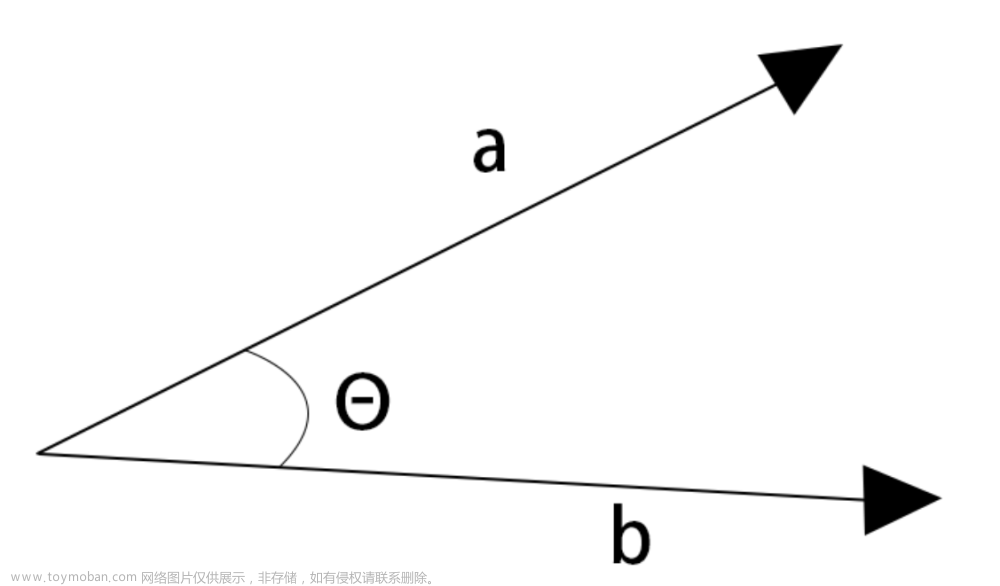
使用叉积进行正交化


如上图所示 使用叉积对三个向量进行正交化 即 先以其中一个向量v0为基础 求出它与v1的叉积w2,由于叉积本身的性质,此时w2已经与v0 v1 两两正交了,然后再求 w2 与 w0的叉积,就得到了第三个向量
值得注意的是 在进行正交化的过程中,我们可以发现除了我们选为基础的向量,其余的向量的方向都可能发生变化,比如在求相机坐标系的三个基向量时候,我们不想改变相机观察向量的方向,此时我们就可以将该向量设置为起始向量,这样该向量的方向就不会改变
矩阵与矩阵乘法
directx采用行主序矩阵
在进行向量与矩阵的乘法运算时,directx这里采用行向量左乘的形式表达:
最终可以化简成,向量中每个系数依次与矩阵的每个行向量进行线性组合
转置矩阵 单位矩阵 逆矩阵 矩阵行列式
略
变换
关于变换的大部分知识games101中已经涵盖 这里就不多赘述
这里主要记录下旋转矩阵与坐标变换
旋转矩阵
这里介绍绕任意轴旋转$\theta $角的公式推导:
如上图所示 黑色的v向量绕着蓝色的k向量旋转$\theta $角,我们可以把v向量分解为垂直于k轴与平行于k轴两部分,在旋转的过程中,平行于k轴的部分不变,而垂直于k轴的向量发生改变。
平行于k轴的向量可表示为:
垂直于k轴的向量即可表示为原向量减去平行向量:
垂直向量旋转$\theta $角 如上图的红色向量所示 可分解为:
最后的旋转向量 就等于旋转之后的垂直向量 再加上平行向量:
然后将其转换为矩阵形式(这里可以利用叉积的矩阵表示):
坐标变换
其实对几何体进行变换与坐标变换在数学上是等价的:
如上图所示
一种是从几何体的平移 旋转的视角来理解(几何体的坐标发生变化)
一种是从坐标系的变换来理解(即基向量的变换,坐标不变,坐标系变化)
我们可以根据不同的场景 选择不同的角度去理解
利用DirectXMath库进行向量运算、矩阵运算以及空间变换
头文件与命名空间
#include <windows.h> // for XMVerifyCPUSupport
#include <DirectXMath.h>
#include <DirectXPackedVector.h>
#include <iostream>
using namespace std;
using namespace DirectX;
using namespace DirectX::PackedVector;
核心向量类型 XMVECTOR
#if defined(_XM_SSE_INTRINSICS_) && !defined(_XM_NO_INTRINSICS_)
using XMVECTOR = __m128;
核心向量类型XMVECTOR被定义为_m128这种特殊的SIMD类型,被映射到SIMD寄存器,通过SIMD指令能够一次处理4个32位的浮点数
XMVECTOR型的数据需要使用16字节对齐,这对于全局以及局部变量是自动实现的,对于类的数据成员,建议使用XMFLOAT2/XMFLOAT3/XMFLOAT4类型的结构体来替代,在实际使用时再将其转换为XMVECTOR类型
XMFLOAT3类型的定义:
// 3D Vector; 32 bit floating point components
struct XMFLOAT3
{
float x;
float y;
float z;
XMFLOAT3() = default;
XMFLOAT3(const XMFLOAT3&) = default;
XMFLOAT3& operator=(const XMFLOAT3&) = default;
XMFLOAT3(XMFLOAT3&&) = default;
XMFLOAT3& operator=(XMFLOAT3&&) = default;
constexpr XMFLOAT3(float _x, float _y, float _z) noexcept : x(_x), y(_y), z(_z) {}
explicit XMFLOAT3(_In_reads_(3) const float* pArray) noexcept : x(pArray[0]), y(pArray[1]), z(pArray[2]) {}
};
FMVECTOR GMVECTOR HMVECTOR CMVECTOR XM_CALLCONV
在进行参数的传递时,我们可以直接将XMVECTOR的值作为参数传给寄存器,而不是存储于栈内,同时为了适应不同的平台与编译器,定义了FMVECTOR GMVECTOR HMVECTOR CMVECTOR四种类型,可以根据不同的平台与编译器定义为不同的类型。
传递规则如下图:
书上举了两个例子加以说明:

注意:
(1)这里的数量统计统计的是XMVECTOR类型的参数,而不是其它类型的参数
(2)定义函数要加上XM_CALLCONV 注解
对于win32来说:
而XM_CALLCONV 则是定义调用约定的:
#if _XM_VECTORCALL_
#define XM_CALLCONV __vectorcall
#elif defined(__GNUC__)
#define XM_CALLCONV
#else
#define XM_CALLCONV __fastcall
#endif
(3) 对于构造函数, 只要針對前三個 XMVECTOR 值使用 FXMVECTOR,然後針對其餘值使用 CXMVECTOR
(4) 对于输出参数,一律使用 XMVECTOR* 或 XMVECTOR& ,因为此时它们不使用寄存器,和其它非XMVECTOR类型的参数一致
其余更为详细的说明可查看:https://learn.microsoft.com/zh-tw/windows/win32/dxmath/pg-xnamath-internals
XMFLOAT 与 XMVECTOR之间的相互转换
以float3为例
vector到float3:
inline void XM_CALLCONV XMStoreFloat3
(
XMFLOAT3* pDestination,
FXMVECTOR V
)
ostream& XM_CALLCONV operator << (ostream& os, FXMVECTOR v)
{
XMFLOAT3 dest;
XMStoreFloat3(&dest, v);
os << "(" << dest.x << ", " << dest.y << ", " << dest.z << ")";
return os;
}
float3到vector:
inline XMVECTOR XM_CALLCONV XMLoadFloat3(const XMFLOAT3* pSource)
XMVECTOR test = XMLoadFloat3(&dest);
向量的初始化
我们可以采用多种方法对向量进行初始化定义:
// x,y,z,w全部初始化为0
XMVECTOR p = XMVectorZero();
// x,y,z,w全部初始化为1
XMVECTOR q = XMVectorSplatOne();
// 使用四个值来初始化向量
XMVECTOR u = XMVectorSet(1.0f, 2.0f, 3.0f, 0.0f);
// 使用一个值初始化向量的四个值
XMVECTOR v = XMVectorReplicate(-2.0f);
// 使用某个向量的一个方向的值初始化向量的四个值
XMVECTOR w = XMVectorSplatZ(u);
向量的运算
运算符的重载:
// Vector addition: XMVECTOR operator +
XMVECTOR a = u + v;
// Vector subtraction: XMVECTOR operator -
XMVECTOR b = u - v;
// Scalar multiplication: XMVECTOR operator *
XMVECTOR c = 10.0f*u;
向量运算(点积,叉积,单位化等):
//计算向量的长度
XMVECTOR L = XMVector3Length(u);
//求对应的单位向量
XMVECTOR d = XMVector3Normalize(u);
//向量之间的点积
XMVECTOR s = XMVector3Dot(u, v);
//向量之间的叉积
XMVECTOR e = XMVector3Cross(u, v);
//求向量w在单位向量n上的投影向量以及垂直向量
XMVECTOR projW;
XMVECTOR perpW;
XMVector3ComponentsFromNormal(&projW, &perpW, w, n);
// 判断向量之间是否相等
bool equal = XMVector3Equal(projW + perpW, w) != 0;
bool notEqual = XMVector3NotEqual(projW + perpW, w) != 0;
// 计算向量之间的角度
// 计算的是弧度制的数值结果
XMVECTOR angleVec = XMVector3AngleBetweenVectors(projW, perpW);
float angleRadians = XMVectorGetX(angleVec);
//转换为角度
float angleDegrees = XMConvertToDegrees(angleRadians);
其它运算:
// 输出向量v的每个组件的绝对值
cout << "XMVectorAbs(v) = " << XMVectorAbs(v) << endl;
// 输出向量w的每个组件的余弦值
cout << "XMVectorCos(w) = " << XMVectorCos(w) << endl;
// 输出向量u的每个组件的自然对数
cout << "XMVectorLog(u) = " << XMVectorLog(u) << endl;
// 输出向量p的每个组件的指数(e的指数)
cout << "XMVectorExp(p) = " << XMVectorExp(p) << endl;
// 输出向量u和向量p对应组件的幂次运算结果
cout << "XMVectorPow(u, p) = " << XMVectorPow(u, p) << endl;
// 输出向量u的每个组件的平方根
cout << "XMVectorSqrt(u) = " << XMVectorSqrt(u) << endl;
// 输出向量u的组件重新排列为(z, z, y, w)的结果
cout << "XMVectorSwizzle(u, 2, 2, 1, 3) = " << XMVectorSwizzle(u, 2, 2, 1, 3) << endl;
// 输出向量u的组件重新排列为(z, y, x, w)的结果
cout << "XMVectorSwizzle(u, 2, 1, 0, 3) = " << XMVectorSwizzle(u, 2, 1, 0, 3) << endl;
// 输出向量u和向量v对应组件的乘积
cout << "XMVectorMultiply(u, v) = " << XMVectorMultiply(u, v) << endl;
// 输出向量q的每个组件限制在[0, 1]范围内的结果
cout << "XMVectorSaturate(q) = " << XMVectorSaturate(q) << endl;
// 输出向量p和向量v对应组件的最小值
cout << "XMVectorMin(p, v) = " << XMVectorMin(p, v) << endl;
// 输出向量p和向量v对应组件的最大值
cout << "XMVectorMax(p, v) = " << XMVectorMax(p, v) << endl;
get方法:

注意上述有些向量运算的结果(比如两个向量之间的点积等等)应该是个标量,但是这里仍然使用XMVECTOR来存储,将标量的结果复制到XMVECTOR的各个分量之中,这样做是为了尽可能降低SIMD向量与标量的混合运算次数,提高计算效率
XMMATRIX定义与初始化
一般情况下 XMMATRIX是由XMVECTOR数组构成:
XMVECTOR r[4];
初始化:
// 采用四个XMVECTOR初始化
constexpr XMMATRIX(FXMVECTOR R0, FXMVECTOR R1, FXMVECTOR R2, CXMVECTOR R3) noexcept : r{ R0,R1,R2,R3 } {}
// 采用4x4个浮点数初始化
XMMATRIX(float m00, float m01, float m02, float m03,
float m10, float m11, float m12, float m13,
float m20, float m21, float m22, float m23,
float m30, float m31, float m32, float m33) noexcept;
// 采用大小为16的浮点数数组初始化
explicit XMMATRIX(_In_reads_(16) const float* pArray) noexcept;
除了上述构造函数的方法,我们也可以使用set函数来初始化:
inline XMMATRIX XM_CALLCONV XMMatrixSet
(
float m00, float m01, float m02, float m03,
float m10, float m11, float m12, float m13,
float m20, float m21, float m22, float m23,
float m30, float m31, float m32, float m33
) noexcept
XMMATRIX FXMMATRIX CXMMTRIX
在声明具有XMMATRIX的参数时,第一个XMMATRIX参数应当为FXMMATRIX,其余应为CXMMATRIX

由于一个XMMATRIX矩阵看作四个XMVECTOR参数,所以在fastcall调用约定下,矩阵类型的数据都是通过堆栈加以引用,在vectorcall调用约定下,FXMMATRIX可以传至寄存器
注意对于构造函数来说,总是采用CXMMATRIX类型来获取XMMATRIX参数,不需要使用XM_CALLCONV注解
同时,对于自定义类中的矩阵类型的数据成员,建议使用XMFLOAT4X4来存储类中的矩阵。
XMFLOAT4X4与XMMATRIX之间的相互转换:

矩阵操作的常用函数
//初始化矩阵
XMMATRIX A(1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 2.0f, 0.0f, 0.0f,
0.0f, 0.0f, 4.0f, 0.0f,
1.0f, 2.0f, 3.0f, 1.0f);
//将矩阵初始化为单位阵
XMMATRIX B = XMMatrixIdentity();
// 矩阵乘法
XMMATRIX C = A * B;
//矩阵转置
XMMATRIX D = XMMatrixTranspose(A);
//求矩阵的行列式
XMVECTOR det = XMMatrixDeterminant(A);
//求矩阵的逆
XMMATRIX E = XMMatrixInverse(&det, A);
空间变换


 文章来源:https://www.toymoban.com/news/detail-825257.html
文章来源:https://www.toymoban.com/news/detail-825257.html
 文章来源地址https://www.toymoban.com/news/detail-825257.html
文章来源地址https://www.toymoban.com/news/detail-825257.html
到了这里,关于d3d12龙书阅读----数学基础 向量代数、矩阵代数、变换的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!