单调队列
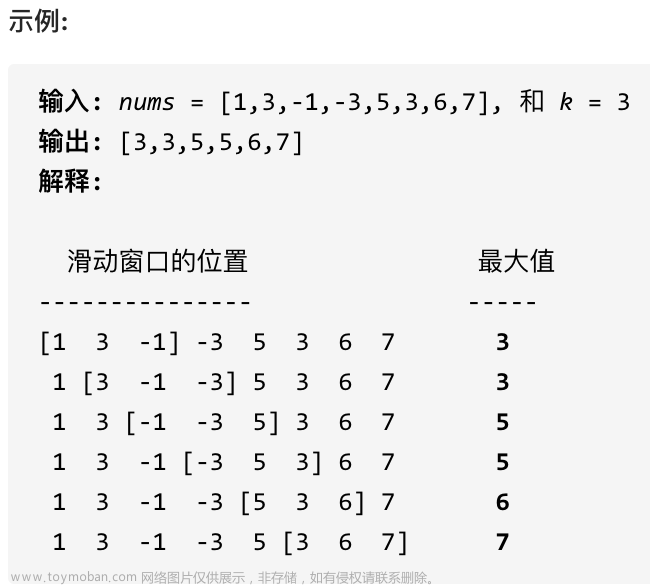
239. 滑动窗口最大值
int *maxSlidingWindow(int *nums, int numsSize, int k, int *returnSize) {
*returnSize = numsSize - k + 1;
int *res = (int *) malloc(sizeof(int) * (*returnSize));
// 双端队列,从大到小排,记录在nums中的下标
int dequeue[100001];
int front = 0, rear = 0;
// 先把窗口扩大到k-1
for (int i = 0; i < k - 1; ++i) {
// 小于等于nums[i]的全部从队尾出队
while (front < rear && nums[dequeue[rear - 1]] <= nums[i])
rear--;
// 入队
dequeue[rear++] = i;
}
for (int l = 0, r = k - 1; l < *returnSize; l++, r++) {
// 小于等于nums[r]的全部从队尾出队
while (front < rear && nums[dequeue[rear - 1]] <= nums[r])
rear--;
// 入队
dequeue[rear++] = r;
// 记录最大值,dequeue开头放的就是最大值在nums中的下标
res[l] = nums[dequeue[front]];
// 若从窗口移除的刚好就是这个最大值,则将其从dequeue中移除
if (dequeue[front] == l) front++;
}
return res;
}
1438. 绝对差不超过限制的最长连续子数组
int minDeque[100001];
int maxDeque[100001];
int maxFront, maxRear, minFront, minRear;
int *arr;
int max(int a, int b) {
return a > b ? a : b;
}
int min(int a, int b) {
return a > b ? b : a;
}
// 子数组中任意两个元素差值不大于limit转换为最大值和最小值的差值不大于limit
bool ok(int limit, int number) {
// 队列为空,number就作为最大值;否则,比较队列中的记录的当前窗口最大值和number
int MAX = maxFront < maxRear ? max(arr[maxDeque[maxFront]], number) : number;
int MIN = minFront < minRear ? min(arr[minDeque[minFront]], number) : number;
return MAX - MIN <= limit;
}
void push(int r) {
// 队列中小于等于arr[r]的从队尾出队
while (maxFront < maxRear && arr[maxDeque[maxRear - 1]] <= arr[r]) maxRear--;
// 入队
maxDeque[maxRear++] = r;
while (minFront < minRear && arr[minDeque[minRear - 1]] >= arr[r]) minRear--;
minDeque[minRear++] = r;
}
void pop(int l) {
// 滑动窗口移除的刚好是最大元素,则将其从队列中移除
if (maxFront < maxRear && maxDeque[maxFront] == l) maxFront++;
if (minFront < minRear && minDeque[minFront] == l) minFront++;
}
int longestSubarray(int *nums, int numsSize, int limit) {
maxFront = 0, maxRear = 0, minFront = 0, minRear = 0;
arr = nums;
int res = 0;
// 窗口[l, r)
for (int l = 0, r = 0; l < numsSize; ++l) {
while (r < numsSize && ok(limit, nums[r])) push(r++);
// 退出循环时,[l, r-1]是以l开头的子数组向右延申的最大范围
res = max(res, r - l);
// 移除l,尝试从下个位置开始往右延申
pop(l);
}
return res;
}
P2698 [USACO12MAR] Flowerpot S
// 接取落水的最小花盆
// 老板需要你帮忙浇花。给出 N 滴水的坐标,y 表示水滴的高度,x 表示它下落到 x 轴的位置
// 每滴水以每秒1个单位长度的速度下落。你需要把花盆放在 x 轴上的某个位置
// 使得从被花盆接着的第 1 滴水开始,到被花盆接着的最后 1 滴水结束,之间的时间差至少为 D
// 我们认为,只要水滴落到 x 轴上,与花盆的边沿对齐,就认为被接住
// 给出 N 滴水的坐标和 D 的大小,请算出最小的花盆的宽度 W
// 测试链接 : https://www.luogu.com.cn/problem/P2698
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的code,提交时请把类名改成"Main",可以直接通过
import java.io.*;
import java.util.Arrays;
class Main {
public static int MAXN = 100005;
public static int[][] arr = new int[MAXN][2];
public static int n, d;
public static int[] maxDeque = new int[MAXN];
public static int[] minDeque = new int[MAXN];
public static int maxh, maxt, minh, mint;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
in.nextToken();
d = (int) in.nval;
for (int i = 0; i < n; i++) {
in.nextToken();
arr[i][0] = (int) in.nval;
in.nextToken();
arr[i][1] = (int) in.nval;
}
int ans = compute();
out.println(ans == Integer.MAX_VALUE ? -1 : ans);
}
out.flush();
out.close();
br.close();
}
public static int compute() {
// arr[0...n-1][2]: x(0), 高度(1)
// 所有水滴根据x排序,谁小谁在前
Arrays.sort(arr, 0, n, (a, b) -> a[0] - b[0]);
maxh = maxt = minh = mint = 0;
int ans = Integer.MAX_VALUE;
for (int l = 0, r = 0; l < n; l++) {
// [l,r) : 水滴的编号
// l : 当前花盘的左边界,arr[l][0]
while (!ok() && r < n) {
push(r++);
}
if (ok()) {
ans = Math.min(ans, arr[r - 1][0] - arr[l][0]);
}
pop(l);
}
return ans;
}
// 当前窗口 最大值 - 最小值 是不是>=d
public static boolean ok() {
int max = maxh < maxt ? arr[maxDeque[maxh]][1] : 0;
int min = minh < mint ? arr[minDeque[minh]][1] : 0;
return max - min >= d;
}
public static void push(int r) {
while (maxh < maxt && arr[maxDeque[maxt - 1]][1] <= arr[r][1]) {
maxt--;
}
maxDeque[maxt++] = r;
while (minh < mint && arr[minDeque[mint - 1]][1] >= arr[r][1]) {
mint--;
}
minDeque[mint++] = r;
}
public static void pop(int l) {
if (maxh < maxt && maxDeque[maxh] == l) {
maxh++;
}
if (minh < mint && minDeque[minh] == l) {
minh++;
}
}
}
862. 和至少为 K 的最短子数组
int min(int a, int b) {
return a > b ? b : a;
}
int shortestSubarray(int *nums, int numsSize, int k) {
int res = 0x7fffffff;
// 单调队列:记录前缀和的下标,前缀和按从小到大排列
int minDeque[100002];
int front = 0, rear = 0;
long long prefixSums[numsSize + 1];
minDeque[rear++] = 0;
prefixSums[0] = 0;
for (int i = 1; i <= numsSize; ++i) {
// 计算前缀和
prefixSums[i] = prefixSums[i - 1] + nums[i - 1];
// 窗口右边进入
// 大于等于当前前缀和的元素从队尾出队
while (front < rear && prefixSums[minDeque[rear - 1]] >= prefixSums[i])
rear--;
// 前缀和下标入队
minDeque[rear++] = i;
// 窗口左边移出
while (front + 1 < rear && prefixSums[i] - prefixSums[minDeque[front + 1]] >= k)
front++;
// 更新符合条件的子数组的最小长度
if (front < rear && prefixSums[i] - prefixSums[minDeque[front]] >= k)
res = min(res, i - minDeque[front]);
}
return res == 0x7fffffff ? -1 : res;
}
1499. 满足不等式的最大值
int max(int a, int b) {
return a > b ? a : b;
}
// 所有的点已按照x坐标递增排序
int findMaxValueOfEquation(int **points, int pointsSize, int *pointsColSize, int k) {
int maxDeque[100001][2];
int front = 0, rear = 0;
int res = 0x80000000;
for (int i = 0, x, y; i < pointsSize; ++i) {
// 查找之前的点,找出y-x的值最大,且x距离不超过k
x = points[i][0];
y = points[i][1];
// x距离超过k的从队头出队
while (front < rear && maxDeque[front][0] + k < x) front++;
// 更新最大值
if (front < rear) res = max(res, x + y + maxDeque[front][1] - maxDeque[front][0]);
// 小于等于当前指标y-x的点都从队尾出队
while (front < rear && maxDeque[rear - 1][1] - maxDeque[rear - 1][0] <= y - x) rear--;
// 当前坐标入队
maxDeque[rear][0] = x;
maxDeque[rear++][1] = y;
}
return res;
}
2071. 你可以安排的最多任务数目
int *tasks;
int *workers;
int tasksSize;
int workersSize;
int deque[50001];
int front, rear;
int cmp(const void *a, const void *b) {
return *(int *) a - *(int *) b;
}
int min(int a, int b) {
return a > b ? b : a;
}
// tasks[tl....tr]需要力量最小的几个任务
// workers[wl....wr]力量值最大的几个工人
// 返回在药的数量不超情况下,任务是否全部都能完成
bool f(int tl, int tr, int wl, int wr, int strength, int pills) {
front = 0;
rear = 0;
// 已使用的药的数量
int count = 0;
// i为工人编号,j为任务编号
for (int i = wl, j = tl; i <= wr; ++i) {
// 当前工人不吃药的情况下,能处理的任务全都入队
while (j <= tr && tasks[j] <= workers[i])
deque[rear++] = j++;
if (front < rear && tasks[deque[front]] <= workers[i]) {
// 不吃药的情况下,完成所需能力最小的那个任务,即队头任务
front++;
} else {
// 不吃药啥也干不了,在吃药的情况下,能处理的任务全都入队
while (j <= tr && tasks[j] <= workers[i] + strength)
deque[rear++] = j++;
if (front < rear) {
// 吃药总数加一
count++;
// 吃了药就要完成难度尽量大的任务,即队尾任务
rear--;
} else {
// 队列空,说明吃了药还是啥都干不了,n个任务,n个工人,有工人干不了活,说明任务无法全部处理
return false;
}
}
}
// 药量够不够
return count <= pills;
}
int maxTaskAssign(int *task, int taskSize, int *worker, int workerSize, int pills, int strength) {
tasks = task;
workers = worker;
tasksSize = taskSize;
workersSize = workerSize;
// 排序方便对应工人和任务
qsort(tasks, tasksSize, sizeof(int), cmp);
qsort(workers, workersSize, sizeof(int), cmp);
int left = 0, right = min(tasksSize, workersSize), mid;
// 右边界
while (left <= right) {
mid = left + (right - left) / 2;
if (f(0, mid - 1, workersSize - mid, workersSize - 1, strength, pills))
left = mid + 1;
else
right = mid - 1;
}
return right;
}
文章来源地址https://www.toymoban.com/news/detail-825348.html
文章来源:https://www.toymoban.com/news/detail-825348.html
到了这里,关于单调队列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!