一、题目
We define the string base to be the infinite wraparound string of “abcdefghijklmnopqrstuvwxyz”, so base will look like this:
“…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd…”.
Given a string s, return the number of unique non-empty substrings of s are present in base.
Example 1:
Input: s = “a”
Output: 1
Explanation: Only the substring “a” of s is in base.
Example 2:
Input: s = “cac”
Output: 2
Explanation: There are two substrings (“a”, “c”) of s in base.
Example 3:
Input: s = “zab”
Output: 6
Explanation: There are six substrings (“z”, “a”, “b”, “za”, “ab”, and “zab”) of s in base.
Constraints:文章来源:https://www.toymoban.com/news/detail-825860.html
1 <= s.length <= 105
s consists of lowercase English letters.文章来源地址https://www.toymoban.com/news/detail-825860.html
二、题解
class Solution {
public:
int findSubstringInWraproundString(string s) {
int n = s.size();
vector<int> a(n,0);
for(int i = 0;i < n;i++){
a[i] = s[i] - 'a';
}
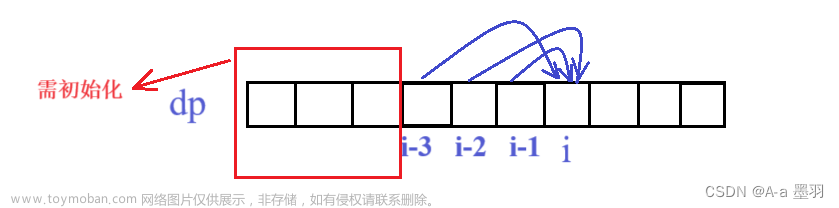
//dp[0]代表s中以a结尾的子串,最大延伸长度是多少(根据base串规则)
vector<int> dp(26,0);
dp[a[0]] = 1;
int len = 1;
for(int i = 1;i < n;i++){
int cur = a[i],pre = a[i-1];
if((pre == 25 && cur == 0) || pre == cur - 1) len++;
else len = 1;
dp[cur] = max(dp[cur],len);
}
int res = 0;
for(int i = 0;i < 26;i++){
res += dp[i];
}
return res;
}
};
到了这里,关于LeetCode467. Unique Substrings in Wraparound String——动态规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!