【数据结构与算法】图的搜索——广度优先遍历、最小生成树-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构与算法】图的搜索——广度优先遍历、最小生成树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

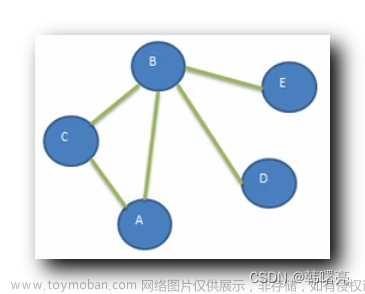
图的表示

邻接链表: 用字典实现.有向图的邻接链表的总长度等于图的边个数;无向图的邻接链表的总长度等于图的边个数的2倍.
邻接矩阵:用于最短路径算法.

Disjoint Set 数据结构

该数据结构维护一个不相交动态集的集合，每个集合有一个代表，不关心谁做代表。
支持三种操作：
MAKE_SET(x)
FIND_SET(x)
UNION(x,y)

应用

确定无向图的连通分量：

MAKE_CONNECTED_COMPONENTS(G):
  for each v in G.V:
    MAKE_SET(v)
  for each (u,v) in G.E:
    if FIND_SET(u) != FIND_SET(v):
       UNION_SET(u,v)

判断无向图中两个结点是否在同一个连通分量：

IS_SAME_COMPONENTS(u,v):
  return FIND_SET(u) == FIND_SET(v)

链表表示

一个链表对应一个子集，链表头包含head和tail属性，head指向第一个对象，tail指向最后一个对象。
合并操作的耗时分析

struct Obj;

struct LinkedList{
  LinkedList(char n) {}
  Obj* head;
  Obj* tail;
};

struct Obj{
  char n;
  Obj* next;
  LinkedList* ll;
};

有根树表示

每棵树的根包含集合的代表。
使用启发式策略实现合并操作
首先，增加rank属性，

MAKE_SET(x):
  x.p = x
  x.rank = 0

UNION(x,y):
  LINK(FIND_SET(x), FIND_SET(y))

LINK(u,v):
if u.rank > v.rank:
  v.p = u
else:
  u.p = v
  if u.rank == v.rank:
    v.rank += 1

带有路径压缩的FIND_SET

FIND_SET(x):
if x.p != x:
  x.p = FIND_SET(x.p)
return x.p

图的搜索算法

图搜索算法是一些图算法的开始步骤,或被优化成其他的图算法.

广度优先遍历

使用队列，先进后出遍历节点，使用节点内的一个变量记录其是否已被遍历，图采用邻接链表形式输入

Col = enum.Enum("Color", ("White", "Gray", "Black"))

class Vertex:
    def __init__(self, u, col, pi):
        self._cnt += 1
        self.u = u
        self.col = col
        self.pi = pi
        self.d = math.inf
    
    def __repr__():
        return "%s"%self.u
def BFS(G, s):
    #初始化初节点s外，其他节点均标记为为被访问，深度设为无穷大
    s.col = Gray
    s.d = 0
    s.pi = None
    Q = []
    while Q:
        u = Q.pop(0)
        for i in G[u]:
            if i.col == Col.White:
                i.col = Col.Gray
                i.d = u.d + 1
                i.pi = u
                Q.append(i)
        u.col = Col.Black

BFS同时生成广度优先搜索树,对于每个从源结点s到可以到达的结点v,广度优先搜索树中从源结点s到结点v的简单路径即图中从s到v的最短路径.该算法可以用于有向图\无向图.
注意权重图暂时无法求其最短路径.

最短路径

打印最短路径
使用广度优先搜索，记录每个节点的前驱

def PrintPath(G,s,e,path=[]):
    if e == s:
        path.append(e)
        print(e)
        return
    if not e.pi:
        print("No path from",s,"to",e)
    else:
        PrintPath(G,s,e.pi,path)
        print(e)
        path.append(e)

深度优先搜索

发现时刻与完成时刻

强连通分量

其指内部两两结点可以相互到达的最大结点集合.

SCC(G):
  DFS(G)
  compute G.T
  按照结点的结束时刻降序遍历的DFS(G.T) 
  返回深度优先搜索森林中的树,即强连通分量

最小生成树

连接所有结点的最小权重的图边集合的子集
求MST的算法采用贪心策略,每一个时刻生长MST的一条边,贪心策略管理的边集合A遵循如下循环不变式:
每次循环前,A是某MST的子集.
安全边:这样的边,加入A后循环不变式仍成立的边.
切割:顶点集的一个划分
横跨切割:一条边的两个结点在两个集合中
轻量级边:满足某指定性质的权重最轻的边
尊重:边集合A中每条边未横跨一切割,称该切割尊重A
安全边定理:A是MST的一个子集,切割尊重A,某边是横跨该切割的轻量级边,则该边是A的安全边.

连通图G中权重最小的一条边(u, v)一定是G的某个最小生成树中的一条边。采用反证法实现，假设(u, v)不是任一个最小生成树中的一条边，设T是一个MST，其中有一个结点x连接u，设R=T-(x,u)，则
$w (T) = w (R) + w (x, u) > w (R) + w (u, v)$
可见T的权重不是最小的生成树，与已知矛盾。文章来源地址https://www.toymoban.com/news/detail-826194.html