【数据结构题目讲解】BZOJ 3306 - 树利用DFS序求解-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构题目讲解】BZOJ 3306 - 树利用DFS序求解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

BZOJ 3306 - 树

D e s c r i p t i o n \mathrm{Description} Description

给定 $1$ 棵以 $1$ 为根节点的 $n$ 个点的树，接下来有 $m$ 次操作：

V x y 将 $x$ 点的权值更改为 $y$
E x 将根改为 $x$ 点
Q x 查询 $x$ 子树的最小值

S o l u t i o n \mathrm{Solution} Solution

首先，考虑如果没有换根操作（即 E 操作），那么直接使用 DFS 序配合线段树的方式即可解决。

DFS 序

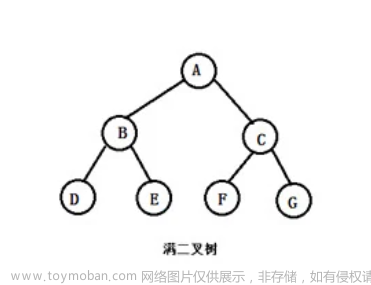
对于 $1$ 棵树的 DFS 序，一个子树在 DFS 序中一定是连续的一个区间：

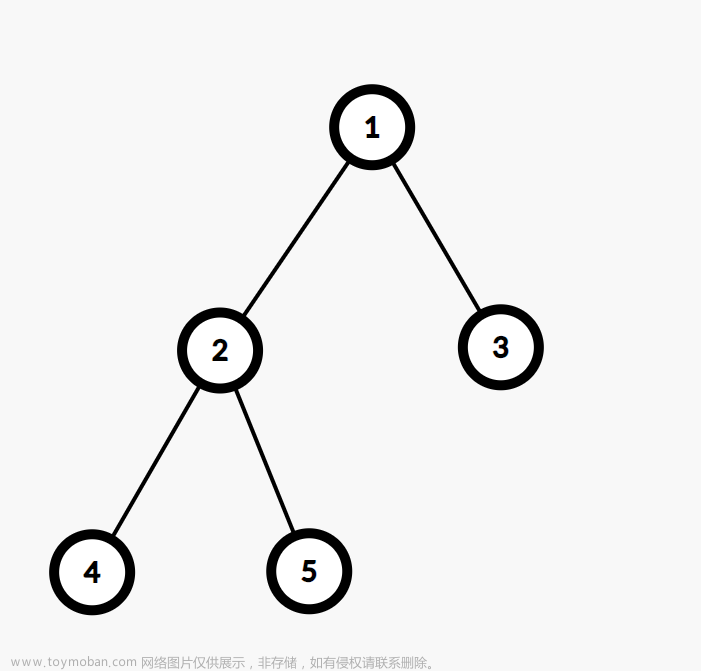
这棵树的 DFS 序即为：1 2 4 5 3（DFS 序就是 DFS 的过程中点访问的先后顺序）

比如说：此时考虑 $2$ 节点的子树，那么在 DFS 序上即为区间 $[2, 4]$ 。也就是说，对于 $i$ 号节点的子树，在 DFS 序上为 $P_i,P_i+Sz_i-1]$ ，其中 $P_i$ 表示 $i$ 节点在 DFS 序中的位置， $Sz_i$ 表示 $i$ 子树的大小。

那么，既然是 $1$ 个区间，所以就可以使用线段树进行快速求解。

那么，就可以由查询子树最小值转化为查询区间最小值。

这时候，考虑换根操作，我们考虑对于某些子树，换根之后，它的子树会不会发生改变。

比如说：

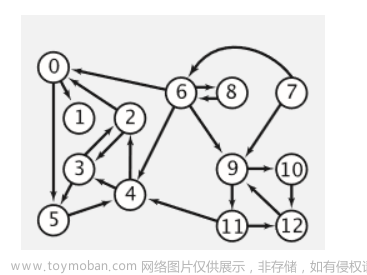
当以 $x$ 为根时， $y$ 子树会发生变化吗？手绘可以发现，其实并不会发生任何变化，所以按照原根进行计算。

那如果 $y$ 在 $x$ 的子树内部呢？

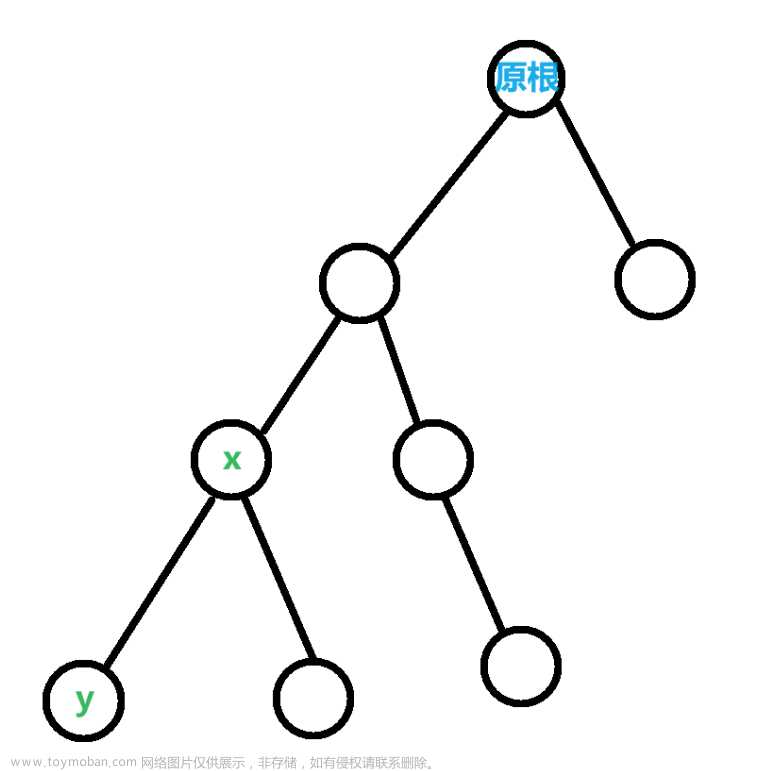
比如说，这样：通过重新画树即可发现，其实 $y$ 的子树根本未发生变化！所以这 $2$ 种位置的子树都不会发生变化。

那，什么时候会发生变化呢？还是说，永远都不会发生变化？

其实，漏考虑了 $1$ 种情况，即为 $y$ 在 $x$ 到原根的路径上：

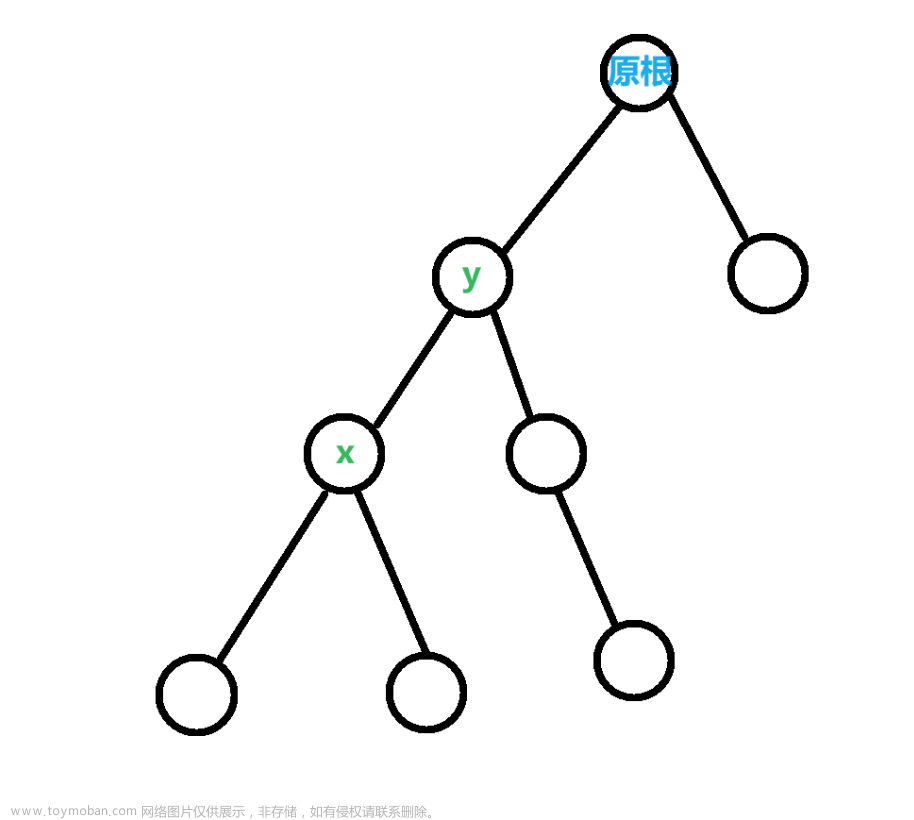
比如说这样，手绘之后发现， $y$ 的子树确实发生变化了，其实就是 $x$ 子树外的部分。

进一步讨论，如果 $y$ 在原根上呢？（图就不给了）这时候其实是少了上图 $y$ 的位置的子树。

综上所述：文章来源地址https://www.toymoban.com/news/detail-826762.html

只有子树的根节点在原根到换之后的根之间的路径上，才会有变化，此时子树为所有点减去 $y$ 到换之后的根之间的路径上与 $y$ 相邻的点 ，即为 $z$ 。（在 DFS 序上其实就是 $2$ 段，即除了 $z$ 子树的部分）
反之，按照原根进行计算即可。

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 1e5 + 10, INF = 1e18;

int N, Q;
int Root, A[SIZE];
std::vector<int> G[SIZE], DFS_Order;
int Depth[SIZE], Fa[SIZE][32], Pos[SIZE], Sz[SIZE];

void BFS(int root)
{
    memset(Depth, 0x3f, sizeof Depth);
    queue<int> q;
    q.push(root);
    Depth[0] = 0, Depth[root] = 1;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (auto j : G[t])
            if (Depth[j] > Depth[t] + 1)
            {
                Depth[j] = Depth[t] + 1;
                q.push(j);
                Fa[j][0] = t;
                for (int k = 1; k <= 22; k ++)
                    Fa[j][k] = Fa[Fa[j][k - 1]][k - 1];
            }
    }
}

int LCA(int a, int b)
{
	if (Depth[a] < Depth[b]) swap(a, b);
    for (int k = 22; k >= 0; k --)
        if (Depth[Fa[a][k]] >= Depth[b])
            a = Fa[a][k];

    if (a == b) return a;

    for (int k = 22; k >= 0; k --)
        if (Fa[a][k] != Fa[b][k])
            a = Fa[a][k], b = Fa[b][k];

    return Fa[a][0];
}

void DFS(int u, int fa)
{
	DFS_Order.push_back(u), Pos[u] = DFS_Order.size() - 1;
	Sz[u] = 1;
	for (auto c : G[u])
	{
		if (c == fa) continue;
		DFS(c, u);
		Sz[u] += Sz[c];
	}
}

struct Segment
{
	int l, r;
	int Min;
}Tree[SIZE << 2];

void Pushup(int u)
{
	Tree[u].Min = min(Tree[u << 1].Min, Tree[u << 1 | 1].Min);
}

void Build(int u, int l, int r)
{
	if (l == r)
	{
		Tree[u] = {l, l, A[DFS_Order[l]]};
		return;
	}

	Tree[u] = {l, r};
	int mid = l + r >> 1;
	Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r);
	Pushup(u);
}

void Modify(int u, int x, int d)
{
	if (Tree[u].l == Tree[u].r && Tree[u].l == x)
	{
		Tree[u].Min = d;
		return;
	}

	int mid = Tree[u].l + Tree[u].r >> 1;
	if (mid >= x) Modify(u << 1, x, d);
	else Modify(u << 1 | 1, x, d);
	Pushup(u);
}

int Query(int u, int l, int r)
{
	if (Tree[u].l >= l && Tree[u].r <= r)
		return Tree[u].Min;

	int mid = Tree[u].l + Tree[u].r >> 1, Result = INF;
	if (mid >= l) Result = Query(u << 1, l, r);
	if (mid < r) Result = min(Result, Query(u << 1 | 1, l, r));
	return Result;
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N >> Q;

	int F;
	for (int i = 1; i <= N; i ++)
	{
		cin >> F >> A[i];
		if (!F) Root = i;
		else G[i].push_back(F), G[F].push_back(i);
	}

	BFS(Root);
	DFS_Order.push_back(-1), DFS(Root, -1);
	Build(1, 1, N);

	while (Q --)
	{
		char Op;
		int x, y;

		cin >> Op >> x;

		if (Op == 'V')
		{
			cin >> y;
			Modify(1, Pos[x], y);
		}
		else if (Op == 'E')
			Root = x;
		else
		{
			if (x == Root)
				cout << Query(1, 1, N) << endl;
			else if (LCA(Root, x) == x && Depth[Root] >= Depth[x])
			{
				for (auto v : G[x])
					if (LCA(v, Root) == v && Depth[v] >= Depth[x])
					{
						int Result = INF;
						if (Pos[v] > 1) Result = min(Result, Query(1, 1, Pos[v] - 1));
						if (Pos[v] + Sz[v] <= N) Result = min(Result, Query(1, Pos[v] + Sz[v], N));
						cout << Result << endl;
						break;
					}
			}
			else
				cout << Query(1, Pos[x], Pos[x] + Sz[x] - 1) << endl;
		}
	}

	return 0;
}