【机器学习笔记】4 朴素贝叶斯-Toy模板网

这篇具有很好参考价值的文章主要介绍了【机器学习笔记】4 朴素贝叶斯。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

贝叶斯方法

贝叶斯分类
贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。
朴素贝叶斯分类是这一类算法中最简单的较为常见的算法。
先验概率
根据以往经验和分析得到的概率。我们用𝑃(𝑌)来代表在没有训练数据前假设𝑌拥有的初始概率。
后验概率
根据已经发生的事件来分析得到的概率。以𝑃(𝑌|𝑋)代表假设𝑋成立的情下观察到𝑌数据的概率，因为它反映了在看到训练数据𝑋后𝑌成立的置信度。
联合概率
是指在多元的概率分布中多个随机变量分别满足各自条件的概率。𝑋与𝑌的联合概率表示为𝑃( 𝑋, 𝑌) 、 𝑃(𝑋𝑌) 或𝑃(𝑋∩𝑌) 。
假设𝑋和𝑌都服从正态分布，那么𝑃(𝑋 < 5, 𝑌 < 0)就是一个联合概率，表示 𝑋 < 5, 𝑌 < 0两个条件同时成立的概率。表示两个事件共同发生的概率。
贝叶斯公式
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能
朴素贝叶斯法是典型的生成学习方法。生成方法由训练数据学习联合概率分布 𝑃(𝑋, 𝑌)，然后求得后验概率分布𝑃(𝑌|𝑋)。
具体来说，利用训练数据学习𝑃(𝑋|𝑌)和𝑃(𝑌)的估计，得到联合概率分布：𝑃(𝑋, 𝑌)＝𝑃(𝑋|𝑌) 𝑃(𝑌)

朴素贝叶斯原理

监督学习方法又分生成方法（Generative approach）和判别方法（Discriminative approach）
所学到的模型分别称为生成模型（Generative Model）和判别模型（Discriminative Model)。
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能
朴素贝叶斯法是典型的生成学习方法
生成方法由训练数据学习联合概率分布 𝑃(𝑋, 𝑌)，然后求得后验概率分布𝑃(𝑌|𝑋)。具体来说，利用训练数据学习𝑃(𝑋|𝑌)和𝑃(𝑌)的估计，得到联合概率分布:𝑃(𝑋, 𝑌)＝𝑃(𝑌)𝑃(𝑋|𝑌).概率估计方法可以是极大似然估计或贝叶斯估计。

朴素贝叶斯法的基本假设是条件独立性
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能
C_k代表类别，k代表类别个数。
这是一个较强的假设。由于这一假设，模型包含的条件概率的数量大为减少，朴素贝叶斯法的学习与预测大为简化。因而朴素贝叶斯法高效，且易于实现。其缺点是分类的性能不一定很高。

朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测
我们要求的是𝑃(𝑌|𝑋)，根据生成模型定义我们可以求𝑃(𝑋, 𝑌)和𝑃(𝑌)假设中的特征是条件独立的。这个称作朴素贝叶斯假设。形式化表示为，（如果给定𝑍的情况下，𝑋和𝑌条件独立）：𝑃(𝑋|𝑍) = 𝑃(𝑋|𝑌, 𝑍)。
也可以表示为：𝑃(𝑋, 𝑌|𝑍) = 𝑃(𝑋|𝑍)𝑃(𝑌|𝑍)

用于文本分类的朴素贝叶斯模型，这个模型称作多值伯努利事件模型。
在这个模型中，我们首先随机选定了邮件的类型𝑝(𝑦)，然后一个人翻阅词典的所有词，随机决定一个词是否出现依照概率𝑝(𝑥⁽¹⁾|𝑦)，出现标示为1，否则标示为0 。假设有50000个单词，那么这封邮件的概率可以表示为：
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能

朴素贝叶斯法对条件概率分布作了条件独立性的假设。由于这是一个较强的假设，朴素贝叶斯法也由此得名。具体地，条件独立性假设是：

朴素贝叶斯法分类时，对给定的输入𝑥，通过学习到的模型计算
后验概率分布𝑃( 𝑌 =c_𝑘| 𝑋 = 𝑥) ，将后验概率最大的类作为𝑥的类输
出。根据贝叶斯定理:
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能

朴素贝叶斯案例

假设我们正在构建一个分类器，该分类器说明文本是否与运动(Sports)有关。我们的训练数据有5句话：
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能
我们想要计算句子“A very close game”是 Sports 的概率以及它不是 Sports 的概率。
即𝑃( Sports | a very close game )这个句子的类别是Sports的概率
特征：单词的频率

我们假设一个句子中的每个单词都与其他单词无关。
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能
计算每个类别的先验概率：对于训练集中的给定句子，𝑃 Sports 的概率为⅗。𝑃(Not Sports )是⅖。
然后，在计算𝑃( 𝑔𝑎𝑚𝑒|𝑆𝑝𝑜𝑟𝑡𝑠 )就是“game”有多少次出现在Sports的样本，然后除以sports为标签的文本的单词总数（3+3+5=11）。
因此，( 𝑔𝑎𝑚𝑒|𝑆𝑝𝑜𝑟𝑡𝑠 )=2/11
“close”不会出现在任何sports样本中！那就是说𝑃( 𝑐𝑙𝑜𝑠𝑒|𝑆𝑝𝑜𝑟𝑡𝑠) = 0。
通过使用一种称为拉普拉斯平滑的方法：我们为每个计数加1，因此它永远不会为零。为了平衡这一点，我们将可能单词的数量添加到除数中，因此计算结果永远不会大于1。
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能
拉普拉斯平滑是一种用于平滑分类数据的技术。引入拉普拉斯平滑法来解决零概率问题,通过应用此方法,先验概率和条件概率可以写为

其中𝐾表示类别数量，𝐴表示𝑎_𝑗中不同值的数量通常𝜆 = 1
加入拉普拉斯平滑之后，避免了出现概率为0的情况，又保证了每个值都在0到1的范围内，又保证了最终和为1的概率性质
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能

朴素贝叶斯的代码实现

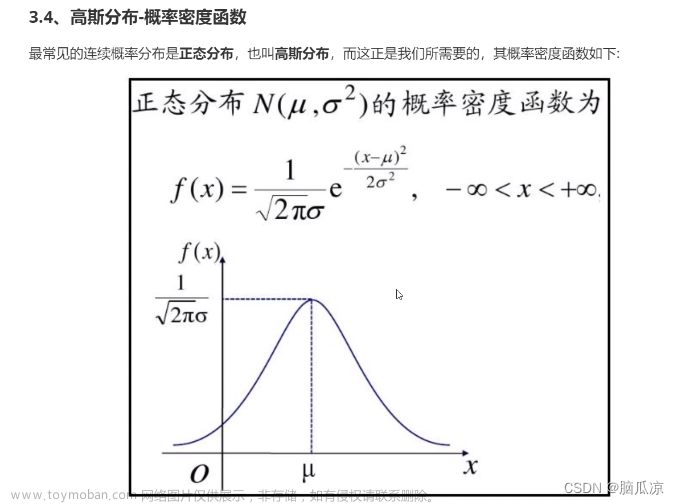
最常用的GaussianNB是高斯贝叶斯分类器。它假设特征的条件概率分布满足高斯分布：
【机器学习笔记】4 朴素贝叶斯,机器学习,机器学习,笔记,人工智能

其他贝叶斯分类器：
MultinomialNB是多项式贝叶斯分类器，它假设特征的条件概率分布满足多项式分布；
BernoulliNB是伯努利贝叶斯分类器。它假设特征的条件概率分布满足二项分布。