uwb最小二乘空间定位+python模拟

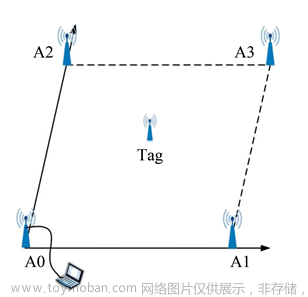
传统最小二乘空间定位原理

假设UWB定位系统里有n个基站。基站坐标设为$(x_i,y_i,z_i)$(i=1,2,3…),标签坐标为（x,y,z),标签到基站的距离设为$d_i(i=1,2,\mathrm{3...})$可得以下关系式
$$\{\begin{array}{l}{\left(x-x_1\right)}^2+{\left(y-y_1\right)}^2+{\left(z-z_1\right)}^2=d_1^2\\ {\left(x-x_2\right)}^2+{\left(y-y_2\right)}^2+{\left(z-z_2\right)}^2=d_2^2\\ \cdots \\ {\left(x-x_n\right)}^2+{\left(y-y_n\right)}^2+{\left(z-z_n\right)}^2=d_n^2\end{array}$$
从第二式开始减去第一式，消去$x^2,y^2,z^2$可得
$$\{\begin{array}{l}({x_2}^2-{x_1}^2)+({y_2}^2-{y_1}^2)+({z_2}^2-{z_1}^2)-2(x_2-x_1)x-2(y_2-y_1)y-2(z_2-z_1)z={d_2}^2-{d_1}^2\\ ({x_3}^2-{x_1}^2)+({y_3}^2-{y_1}^2)+({z_3}^2-{z_1}^2)-2(x_3-x_1)x-2(y_3-y_1)y-2(z_3-z_1)z={d_3}^2-{d_1}^2\\ ⋮\\ ({x_n}^2-{x_1}^2)+({y_n}^2-{y_1}^2)+({z_n}^2-{z_1}^2)-2(x_n-x_1)x-2(y_n-y_1)y-2(z_n-z_1)z={d_n}^2-{d_1}^2\end{array}$$

化成矩阵形式为AX=B
A = 2 [ x 1 − x 2 y 1 − y 2 z 1 − z 2 x 1 − x 3 y 1 − y 3 z 1 − y z 3 ⋮ ⋮ x 1 − x n y 1 − y n z 1 − z n ] \left.A=2\left[\begin{matrix}x_1-x_2 & & y_1-y_2 & z_1-z_2\\ x_1-x_3 & & y_1-y_3 & z_1-yz_3\\ \vdots & & \vdots & \\ x_1-x_{n} & & y_1-y_{n} & z_1-z_{n}\end{matrix}\right.\right] A=2 ​x1​−x2​x1​−x3​⋮x1​−xn​​​y1​−y2​y1​−y3​⋮y1​−yn​​z1​−z2​z1​−yz3​z1​−zn​​ ​
X = [ x y z ] X=\begin{bmatrix}x\\y\\z\end{bmatrix} X= ​xyz​ ​
B = [ d 2 2 − d 1 2 + ( x 1 2 − x 2 2 ) + ( y 1 2 − y 2 2 ) + ( z 1 2 − z 2 2 ) d 3 2 − d 1 2 + ( x 1 2 − x 3 2 ) + ( y 1 2 − y 3 2 ) + ( z 1 2 − z 3 2 ) ⋮ d n 2 − d 1 2 + ( x 1 2 − x n 2 ) + ( y 1 2 − y n 2 ) + ( z 1 2 − z n 2 ) ] \left.B=\left[\begin{matrix}{{d}_{2}}^2-{{d}_{1}}^2+({x_{1}}^2-{x_{2}}^2)+({y_{1}}^2-{y_{2}}^2)+({z_1}^2-{z_2}^2) & \\ {{d}_{3}}^2-{{d}_{1}}^2+({x_{1}}^2-{x_{3}}^2)+({y_{1}}^2-{y_{3}}^2)+({z_1}^2-{z_3}^2) & \\ \vdots & \\ {{d}_{n}}^2-{{d}_{1}}^2+({x_{1}}^2-{x_{n}}^2)+({y_{1}}^2-{y_{n}}^2)+({z_1}^2-{z_{n}}^2) & \end{matrix}\right.\right] B= ​d2​2−d1​2+(x1​2−x2​2)+(y1​2−y2​2)+(z1​2−z2​2)d3​2−d1​2+(x1​2−x3​2)+(y1​2−y3​2)+(z1​2−z3​2)⋮dn​2−d1​2+(x1​2−xn​2)+(y1​2−yn​2)+(z1​2−zn​2)​​ ​

要求X可得
[ x y z ] = 1 2 ( A T A ) − 1 A T B \begin{bmatrix}x\\ y\\ z\end{bmatrix}=\dfrac{1}{2}\Big(A^{T}A\Big)^{-1}A^{T}B ​xyz​ ​=21​(ATA)−1ATB
要求三维坐标至少四个基站

python算法模拟：
这里先模拟二维的，使用最小二乘法求解时，会因基站z轴坐标差值小导致误差较大，相较与水平坐标，z坐标不可靠，故采用其他方法获取z值文章来源地址https://www.toymoban.com/news/detail-827184.html

import tkinter as tk

import numpy as np

import math

import random

import matplotlib.pyplot as plt

  

class MapApp:

    def __init__(self, master):

        self.master = master

        self.master.title("UWB Emulation")

        self.master.geometry("800x600")

  

        self.num_base_stations = 4

        self.base_stations = [(random.randint(50, 550), random.randint(50, 550)) for _ in range(self.num_base_stations)]

        self.noise_mean = 0

        self.noise_stddev = 1

  

        self.canvas = tk.Canvas(self.master, width=600, height=600, bg="white")

        self.canvas.pack(side=tk.LEFT)

  

        self.label = tk.Label(self.master, text="")

        self.label.pack()

  

        self.mouse_marker = None

        self.distance_circles = []

  

        self.create_widgets()

        # 鼠标移动时进行一次计算

        self.canvas.bind("<Motion>", self.show_mouse_position)

  

    def create_widgets(self):

        self.create_base_stations()

        self.create_noise_slider()

  

    def create_base_stations(self):

        i=0

        for station in self.base_stations:

  

            x, y = station

            self.canvas.create_oval(x - 5, y - 5, x + 5, y + 5, fill="red")

             # 在标签中显示每个基站的坐标

            station_label = tk.Label(self.master, text=f"Base Station {i+1}: ({x}, {y})")

            station_label.pack()

            i = i+1

  

    def calculate_distance(self, x, y):

        distances = [math.sqrt((x - station[0])**2 + (y - station[1])**2) + random.gauss(self.noise_mean, self.noise_stddev) for station in self.base_stations]

        return distances

  

    def draw_distance_circles(self, x, y, distances):

        for i, station in enumerate(self.base_stations):

            x0, y0 = station

            radius = distances[i]

            circle = self.canvas.create_oval(x0 - radius, y0 - radius, x0 + radius, y0 + radius, outline="blue")

            self.distance_circles.append(circle)

  
  

    #最小二乘法

  

    def uwb_LeastQusare(self, distance_vector):

        # 创建A矩阵

        x_1, y_1 = self.base_stations[0]

        a = np.array([[x_1 - station[0], y_1 - station[1]] for station in self.base_stations[1:]])

        # 创建B矩阵

        d_1 = distance_vector[0]

        # print('test')

        # print(distance_vector[1]**2 - d_1**2)

        # print(distance_vector[1]**2 - d_1**2 + (x_1**2 - self.base_stations[1][0]**2))

        # print(distance_vector[1]**2 - d_1**2 + (x_1**2 - self.base_stations[1][0]**2) + (y_1**2 - self.base_stations[1][1]**2))

        b = np.array([[distance_vector[i]**2 - d_1**2 + (x_1**2 - station[0]**2) + (y_1**2 - station[1]**2)] for i, station in enumerate(self.base_stations[1:],start=1)])

  

        X = np.dot(np.linalg.inv(np.dot(np.transpose(a), a)), np.dot(np.transpose(a), b)) * 0.5

        # print('aa:')

        # print(a)

        # print('bb:')

        # print(b)

        # print('cc')

        # print(X)

        return X;

  

  

    def show_mouse_position(self, event):

        if self.mouse_marker:

            self.canvas.delete(self.mouse_marker)

        true_val = event.x, event.y

        x, y = event.x, event.y

        distances = self.calculate_distance(x, y)

        distance_text = "\n".join([f"Base Station {i+1}: {dist:.2f}" for i, dist in enumerate(distances)])

        self.label.config(text=f"Mouse Position: ({x}, {y})\nDistances to Base Stations:\n{distance_text}")

        #最小二乘法求解

        result = self.uwb_LeastQusare(distances)

        Err_val = (true_val[0]-result[0])**2 + (true_val[1]-result[1])**2

        print('result'+'     '+str(result))

        print(Err_val)

  

        self.mouse_marker = self.canvas.create_oval(x - 3, y - 3, x + 3, y + 3, fill="green")

  

        for circle in self.distance_circles:

            self.canvas.delete(circle)

        self.distance_circles = []

  

        self.draw_distance_circles(x, y, distances)

  

    def create_noise_slider(self):

        noise_frame = tk.Frame(self.master)

        noise_frame.pack()

  

        noise_label = tk.Label(noise_frame, text="Noise Level:")

        noise_label.pack(side=tk.LEFT)

  

        noise_slider = tk.Scale(noise_frame, from_=0, to=100, resolution=0.1, orient=tk.HORIZONTAL, command=self.update_noise_level)

        noise_slider.pack(side=tk.LEFT)

  

    def update_noise_level(self, value):

        self.noise_stddev = float(value)

  

    def get_distance_values(self):

        # 获取显示在窗口上的距离值

        return self.label["text"]

  
  

def main():

    root = tk.Tk()

    app = MapApp(root)

    root.mainloop()

  

    # 获取显示在窗口上的距离值

    distance_values = app.get_distance_values()

    print("Distance Values:", distance_values)

  

if __name__ == "__main__":

    main()

到了这里，关于uwb最小二乘空间定位+python模拟的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！