一、DFS
往深里搜,搜到叶子结点那里,回溯,到可以继续到叶子结点深搜的位置。
1、回溯一定要恢复现场
2、定义一个与当前递归层数有关的终止条件(题目要求的东西)
3、每层都用循环判断是否存在可以dfs的路
输出数字组合
#include<bits/stdc++.h>
//842排列数字 按照字典序将n个数
using namespace std;
const int N=1e5+10;
int path[N];//记录走过的路径
int st[N];//用来记录某个元素是否被用过
int n;
void dfs(int u)
{
//先判断是否已经得到一个答案
if(u==n)
{
for(int i=0;i<n;i++)cout<<path[i]<<" ";
puts("");
return;
}
for(int i=1;i<=n;i++)
{
if(!st[i])//剪枝的过程找到可以构成dfs路径的方向
{
st[i]=true;
path[u]=i;
dfs(u+1);
path[i]=0;//恢复现场
st[i]=false;
}
}
}
int main()
{
cin>>n;
dfs(0);
return 0;
}
全排列的思想解决n皇后问题,用三个bool数组描述限制条件,用二维char数组保存结果,在恢复现场的时候也要恢复g数组,因为后面的其他结果可能不会将其覆盖掉。
#include<bits/stdc++.h>
//843 n皇后问题(全排列问题)
using namespace std;
const int N=20;
int path[N];//记录走过的路径
char g[N][N];
bool col[N],row[N],dg[N],udg[N];
int n;
void dfs(int u)
{
//先判断是否已经得到一个答案
if(u==n)
{
for(int i=0;i<n;i++)puts(g[i]);
puts("");
return;
}
for(int i=0;i<n;i++)
{
if(!col[i]&&!dg[u+i]&&!udg[n-u+i])
{
g[u][i]='Q';
col[i]=dg[u+i]=udg[n-u+i]=true;
dfs(u+1);
col[i]=dg[u+i]=udg[n-u+i]=false;
g[u][i]='.';
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]='.';
dfs(0);
return 0;
}
按照元素枚举的方式解决n皇后问题
#include<bits/stdc++.h>
//843 n皇后问题(全排列问题)
using namespace std;
const int N=20;
int path[N];//记录走过的路径
char g[N][N];
bool col[N],row[N],dg[N],udg[N];
int n;
void dfs(int x,int y,int u)//x为行,y为列
{
if(y==n)y=0,x++;
if(x==n)
{
if(u==n)//有可能到头了也没有找到全部的皇后
{
for(int i=0; i<n; i++)puts(g[i]);
puts("");
}
return;
}
//为什么要添加xy两个参数
//因为这个思路不是循环式地剪枝,是利用递归进行搜索
//处理坐标
//不放当前位置
dfs(x,y+1,u);
//放当前位置
if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[n-y+x])
{
g[x][y]='Q';
row[x]=col[y]=dg[x+y]=udg[n-y+x]=true;
dfs(x,y+1,u+1);
g[x][y]='.';
row[x]=col[y]=dg[x+y]=udg[n-y+x]=false;
}
}
int main()
{
cin>>n;
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
g[i][j]='.';
dfs(0,0,0);
return 0;
}
二、BFS
一层一层地搜索,如果边都是1,bfs第一次搜到的点具有最短路性质

1、具有最短路性质的原因:因为bfs每次都向外扩展一层,依次找到距离起点为1,2,3的所有点。
#include<bits/stdc++.h>
//844走迷宫//添加路径
using namespace std;
const int N=110;
typedef pair<int,int>PII;
int g[N][N];//存图
int d[N][N];//存距离
PII q[N*N];//模拟队列
PII pre[N][N];//路径的前驱
//由于最短路性质,可以直接将当前节点前的一个结点作为前驱
int n,m;
void bfs()
{
memset(d,-1,sizeof d);//用于判断是否是第一次访问到
//一个点可以有多个路径到达,但是第一个到达的一定是最短路
d[0][0]=0;
int hh=0,tt=0;
q[0]={0,0};
int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};
while(hh<=tt)//只要非空
{
auto t=q[hh++];
for(int i=0;i<4;i++)
{
int x=t.first+dx[i],y=t.second+dy[i];
if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&d[x][y]==-1)
{
d[x][y]=d[t.first][t.second]+1;
q[++tt]={x,y};
pre[x][y]=t;
}
}
}
int x=n-1,y=m-1;
while(x||y)
{
cout<<x<<" "<<y<<endl;
x=pre[x][y].first;
y=pre[x][y].second;
}
}
int main()
{
cin>>n>>m;
for(int i=0; i<n; i++)
for(int j=0; j<m; j++)
cin>>g[i][j];
bfs();
cout<<d[n-1][m-1];
return 0;
}
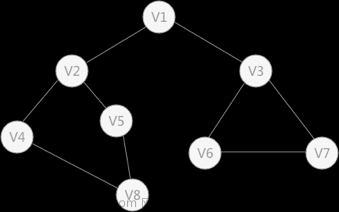
三、邻接表邻接矩阵存图
1、邻接表的存法

2、使用h数组作为槽,利用e和ne数组和idx构造单链表存槽中相应结点有边相连的节点、
根据题意利用从1深搜,每一层用res存最大的子图的点数,每次计算出一个子连通图添加到sum中。
#include<bits/stdc++.h>
//846 树重心
using namespace std;
const int N=1e5+10,M=N*2;
typedef pair<int,int>PII;
int h[N],e[M],ne[M],idx;
bool st[N];
//h保存n个头结点
//在用数组模拟链表时,e保存链表结点值,ne保存边
//idx让这一切有序
int ans=N,n;//存结果
int dfs(int u)//u是结点的名字不是idx性质的
{
st[u]=true;//标记这个结点已经被搜索过了
//在遍历当前节点的所有子树之前
int sum=1;//存所有子树的节点个数
int res=0;//记录各个连通子图的节点个数
for(int i=h[u];i!=-1;i=ne[i])
{
int j =e[i];
if(st[j]==false)//只要这个结点的子树还没计算
{
int t=dfs(j);
res=max(res,t);//存最大连通子图
sum+=t;//所有子树
}
}
res=max(res,n-sum);
ans=min(ans,res);//保存最小的最大连通子图
return sum;
}
void add(int a,int b)//头插法
{
e[idx]=b;//每个idx都代表一个链表上的节点
ne[idx]=h[a];
h[a]=idx++;
}
int main()
{
memset(h,-1,sizeof h);
//memset(st,false,sizeof st);
//所有结点的单链表指向的位置都为空
cin>>n;
for(int i=0;i<n-1;i++)
{
int a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
dfs(1);
cout<<ans<<endl;
}
3、邻接表利用bfs计算最短路文章来源:https://www.toymoban.com/news/detail-827329.html
#include<bits/stdc++.h>
//847图中点的层次
using namespace std;
const int N=1e5+10,M=2*N;
int n,m;
int h[N],e[N],ne[N],idx;
int d[N],q[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{
int hh=0,tt=0;
memset(d,-1,sizeof d);
q[0]=1;//1是结点的名字,入队
d[1]=0;//到第一个结点的距离为0
//数组模拟队列的时候hh永远指向队列的第一个元素,tt永远指向队尾,所以判断队列不为空的判断条件是hh<=tt。
while(hh<=tt)
{
int t=q[hh++];//拿出队头元素
for(int i=h[t];i!=-1;i=ne[i])//遍历与其相连的所有边
{
int j=e[i];//
if(d[j]==-1)
{
d[j]=d[t]+1;
q[++tt]=j;
}
}
}
return d[n];
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
}
cout<<bfs()<<endl;
return 0;
}
4、有向无环图一定有拓扑序列,拓扑排序的实现文章来源地址https://www.toymoban.com/news/detail-827329.html
#include<bits/stdc++.h>
//848拓扑排序
using namespace std;
const int N=1e5+10,M=2*N;
int n,m;
int h[N],e[N],ne[N],idx;
int d[N],q[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool topsort()
{
int hh=0,tt=-1;
for(int i=1;i<=n;i++)
{
if(!d[i])q[++tt]=i;
}
while(hh<=tt)
{
int t=q[hh++];
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
d[j]--;
if(!d[j])q[++tt]=j;
}
}
return tt==n-1;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
d[b]++;
}
if(!topsort())puts("-1");
else
{
for(int i=0;i<n;i++)cout<<q[i]<<" ";
puts("");
}
}
到了这里,关于搜索与图论(一)(深搜,广搜,树与图的存储遍历,拓扑排序)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!