1.背景介绍
1. 背景介绍
强化学习(Reinforcement Learning,RL)是一种机器学习方法,它通过与环境的互动来学习如何做出最佳决策。强化学习的目标是找到一种策略,使得在长期内累积最大化奖励。强化学习的一个关键特点是它需要在环境中探索和利用,以找到最佳的行为策略。
动态规划(Dynamic Programming,DP)和蒙特卡罗方法(Monte Carlo Method)是强化学习中两种常见的方法。动态规划是一种解决最优化问题的方法,它通过将问题分解为子问题来求解。蒙特卡罗方法是一种基于随机样本的方法,它通过生成大量的随机样本来估计解。
在强化学习中,动态规划和蒙特卡罗方法可以用于解决不同类型的问题。动态规划通常用于有模型的问题,即已知环境的状态转移概率和奖励。而蒙特卡罗方法则适用于无模型的问题,即无法得到环境的状态转移概率和奖励。
2. 核心概念与联系
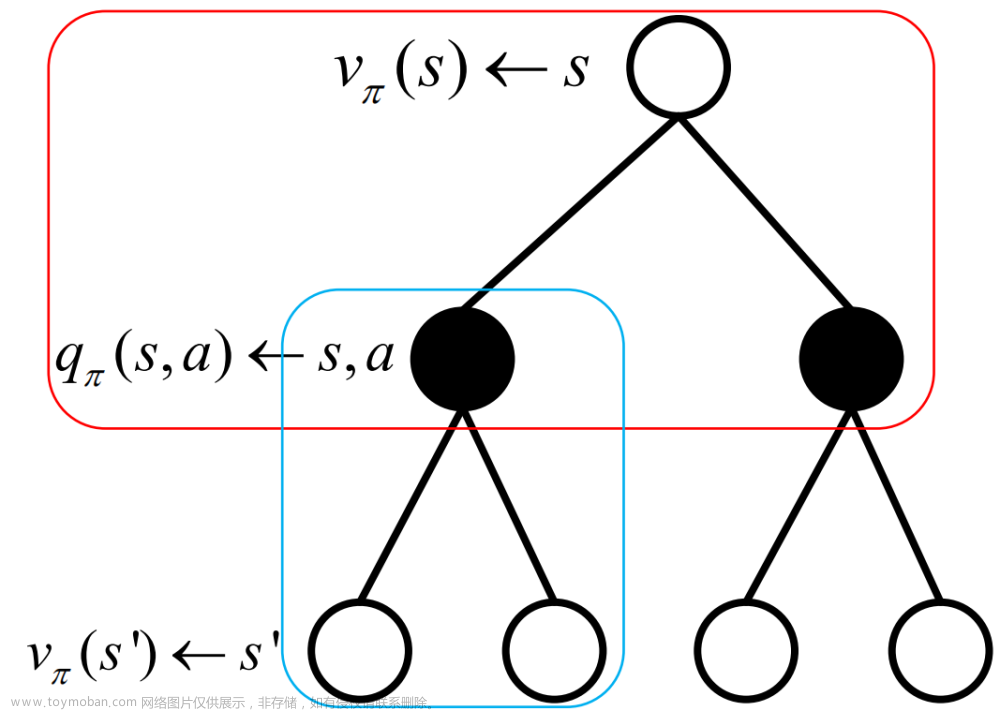
在强化学习中,动态规划和蒙特卡罗方法的核心概念是策略和值函数。策略(Policy)是一个映射从状态到行为的函数,它决定了在给定状态下应该采取哪种行为。值函数(Value Function)是一个映射从状态到期望累积奖励的函数,它用于评估策略的优劣。
动态规划和蒙特卡罗方法的联系在于它们都涉及到值函数的估计。动态规划通过递归地计算状态值函数来得到最优策略,而蒙特卡罗方法则通过生成随机样本来估计状态值函数。
3. 核心算法原理和具体操作步骤以及数学模型公式详细讲解
3.1 动态规划
动态规划(DP)是一种解决最优化问题的方法,它通过将问题分解为子问题来求解。在强化学习中,动态规划通常用于有模型的问题,即已知环境的状态转移概率和奖励。
动态规划的核心思想是将一个复杂问题分解为多个子问题,并解决子问题以求解整个问题。动态规划的算法通常包括以下步骤:
- 初始化:将问题中的所有子问题的解初始化为某种特定值,如0或-∞。
- 递归求解:根据问题的特征,递归地求解子问题的解。
- 合并:将子问题的解合并为整个问题的解。
在强化学习中,动态规划通常用于解决有模型的问题,如Markov Decision Process(MDP)。MDP是一个五元组(S, A, P, R, γ),其中S是状态集,A是行为集,P是状态转移概率,R是奖励函数,γ是折扣因子。
在MDP中,动态规划的目标是找到一种策略,使得在长期内累积最大化奖励。动态规划通过将问题分解为子问题来求解,可以得到最优策略。
3.2 蒙特卡罗方法
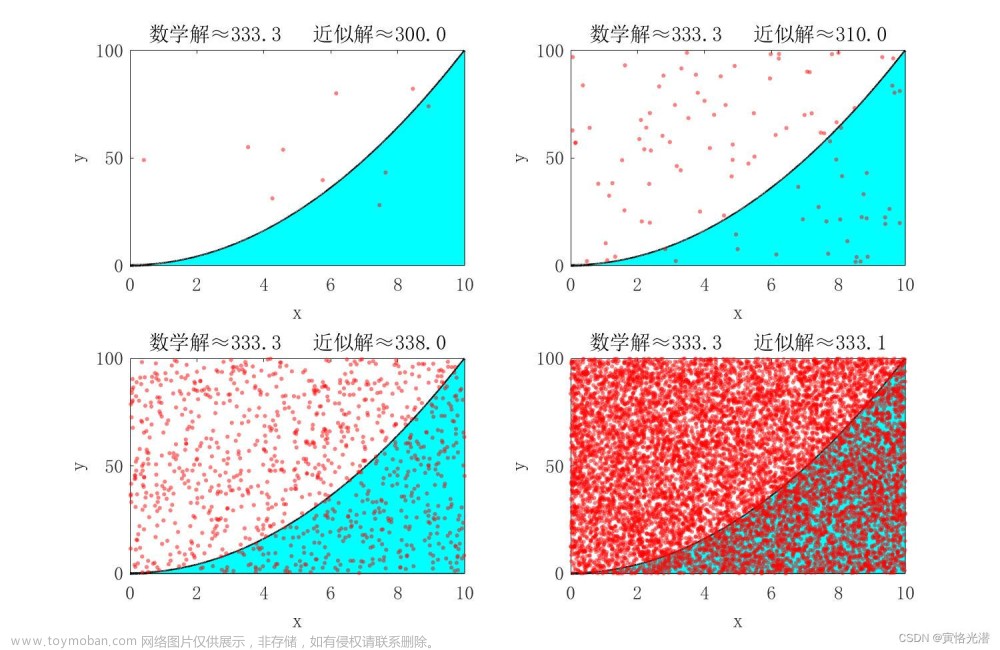
蒙特卡罗方法(Monte Carlo Method)是一种基于随机样本的方法,它通过生成大量的随机样本来估计解。在强化学习中,蒙特卡罗方法适用于无模型的问题,即无法得到环境的状态转移概率和奖励。
蒙特卡罗方法的核心思想是通过生成大量的随机样本来估计解。蒙特卡罗方法的算法通常包括以下步骤:
- 初始化:将问题中的所有参数初始化为某种特定值,如0或均值。
- 生成随机样本:根据问题的特征,生成大量的随机样本。
- 估计:根据随机样本,估计问题的解。
在强化学习中,蒙特卡罗方法通常用于解决无模型的问题,如Deep Q-Network(DQN)和Proximal Policy Optimization(PPO)。蒙特卡罗方法通过生成大量的随机样本来估计解,可以得到近似最优策略。
3.3 数学模型公式详细讲解
3.3.1 动态规划
在MDP中,动态规划的目标是找到一种策略,使得在长期内累积最大化奖励。动态规划通过将问题分解为子问题来求解,可以得到最优策略。
在MDP中,动态规划的核心公式是Bellman方程:
$$ V(s) = \max{a \in A} \left{ \sum{s' \in S} P(s'|s,a) [R(s,a,s') + \gamma V(s')] \right} $$
其中,$V(s)$是状态$s$的值函数,$A$是行为集,$P(s'|s,a)$是从状态$s$采取行为$a$后进入状态$s'$的概率,$R(s,a,s')$是从状态$s$采取行为$a$后进入状态$s'$的奖励,$\gamma$是折扣因子。
通过递归地求解Bellman方程,可以得到最优策略。
3.3.2 蒙特卡罗方法
在无模型的问题中,蒙特卡罗方法通过生成大量的随机样本来估计解。在强化学习中,蒙特卡罗方法的核心公式是:
$$ Q(s,a) \approx \frac{1}{N} \sum{i=1}^{N} \left{ Rt + \gamma \max{a'} Q(s{t+1},a') \right} $$
其中,$Q(s,a)$是状态$s$和行为$a$的Q值,$N$是随机样本的数量,$Rt$是时间$t$的奖励,$s{t+1}$是时间$t+1$的状态,$\gamma$是折扣因子。
通过生成大量的随机样本,可以估计Q值,从而得到近似最优策略。
4. 具体最佳实践:代码实例和详细解释说明
在这里,我们以一个简单的例子来展示动态规划和蒙特卡罗方法在强化学习中的应用。
4.1 动态规划实例
考虑一个简单的环境,有两个状态$s1$和$s2$,两个行为$a1$和$a2$,状态转移概率和奖励如下:
| | $a1$ | $a2$ | | - | - | - | | $s1$ | (0.8, 2) | (0.2, -1) | | $s2$ | (0.5, 1) | (0.5, -2) |
状态转移概率表示从状态$si$采取行为$aj$后进入状态$sk$的概率,奖励表示从状态$si$采取行为$a_j$后获得的奖励。
通过解Bellman方程,可以得到最优策略:
$$ V(s1) = \max{a \in A} \left{ \sum_{s' \in S} P(s'|s,a) [R(s,a,s') + \gamma V(s')] \right} $$
$$ V(s1) = \max{a \in A} \left{ 0.8 \cdot (2 + \gamma V(s1)) + 0.2 \cdot (-1 + \gamma V(s2)) \right} $$
$$ V(s1) = \max{a \in A} \left{ 0.8 \cdot (2 + \gamma V(s1)) + 0.2 \cdot (-1 + \gamma V(s2)) \right} = 1.6 $$
$$ V(s2) = \max{a \in A} \left{ 0.5 \cdot (1 + \gamma V(s1)) + 0.5 \cdot (-2 + \gamma V(s2)) \right} $$
$$ V(s2) = \max{a \in A} \left{ 0.5 \cdot (1 + \gamma V(s1)) + 0.5 \cdot (-2 + \gamma V(s2)) \right} = -0.5 $$
最优策略为:在$s1$时采取$a1$,在$s2$时采取$a1$。
4.2 蒙特卡罗方法实例
考虑同样的环境,通过蒙特卡罗方法估计Q值:
```python import numpy as np
N = 10000 Q = np.zeros((2, 2))
for i in range(N): s = np.random.choice([0, 1]) a = np.random.choice([0, 1]) s_next = np.random.choice([0, 1]) r = np.random.choice([2, -1, 1, -2])
Q[s, a] += (r + gamma * np.max(Q[s_next]))```
通过生成大量的随机样本,可以得到近似的Q值,从而得到近似最优策略。
5. 实际应用场景
动态规划和蒙特卡罗方法在强化学习中有广泛的应用场景,如游戏(Go,Chess)、机器人(自动驾驶,服务机器人)、生物学(神经科学,遗传算法)等。
6. 工具和资源推荐
在学习和应用动态规划和蒙特卡罗方法时,可以参考以下工具和资源:
- 书籍:
- "Reinforcement Learning: An Introduction" by Richard S. Sutton and Andrew G. Barto
- "Monte Carlo Methods in Financial Engineering" by Glynn and Meyn
- 在线课程:
- Coursera:Reinforcement Learning by University of Alberta
- edX:Introduction to Reinforcement Learning by University of Michigan
- 研究论文:
- "Reinforcement Learning: An Introduction" by Richard S. Sutton and Andrew G. Barto
- "Monte Carlo Methods in Financial Engineering" by Glynn and Meyn
- 开源项目:
- OpenAI Gym:https://gym.openai.com/
- TensorFlow Reinforcement Learning:https://www.tensorflow.org/tutorials/reinforcement_learning/cartpole
7. 总结:未来发展趋势与挑战
动态规划和蒙特卡罗方法在强化学习中有着广泛的应用,但仍有许多挑战需要解决。未来的研究方向包括:
- 解决高维状态和动作空间的问题,如深度强化学习。
- 提高强化学习算法的样本效率,如优化蒙特卡罗方法。
- 研究强化学习算法的稳定性和可解释性。
8. 附录:常见问题与解答
Q: 动态规划和蒙特卡罗方法有什么区别? A: 动态规划是一种解决最优化问题的方法,它通过将问题分解为子问题来求解。而蒙特卡罗方法是一种基于随机样本的方法,它通过生成大量的随机样本来估计解。
Q: 在强化学习中,动态规划和蒙特卡罗方法有什么应用? A: 动态规划和蒙特卡罗方法在强化学习中有广泛的应用场景,如游戏、机器人、生物学等。文章来源:https://www.toymoban.com/news/detail-827736.html
Q: 如何选择适合自己的强化学习方法? A: 选择适合自己的强化学习方法需要考虑问题的特征和环境的模型。如果已知环境的状态转移概率和奖励,可以选择动态规划。如果无法得到环境的状态转移概率和奖励,可以选择蒙特卡罗方法。文章来源地址https://www.toymoban.com/news/detail-827736.html
到了这里,关于强化学习中的动态规划与蒙特卡罗方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!