详解数据结构中的堆-Toy模板网

这篇具有很好参考价值的文章主要介绍了详解数据结构中的堆。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

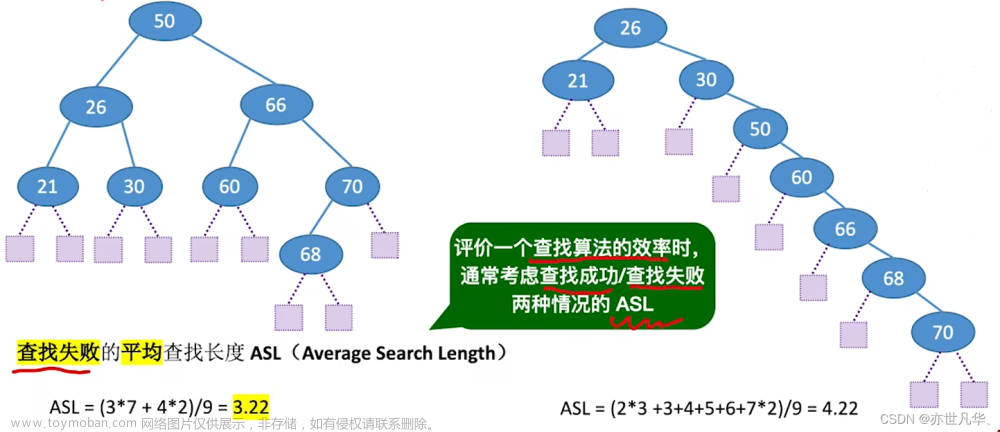
本篇文章主要讲解如何构建一个堆（本文讲的是二叉堆），堆排序以及TOP-K问题。

1.构建堆

首先，储存堆我们用到的是数组，我们把它封装为一个结构体

typedef int HDataType;

typedef struct Heap
{
	HDataType* arr;
	int size;
	int capacity;
}Heap;

size是数组里面有效数据的个数，capacity是数组的容量大小。

虽然堆在物理结构上是一个数组，但在逻辑结构上我们把它想象做一个完全二叉树，如下图
详解数据结构中的堆,数据结构,算法,c语言
这样我们可以通过下标来访问这棵树。
下面是通过父亲访问孩子：
我们定义父节点的下标为parent，那左孩子节点的下标就是parent * 2 + 1，右孩子节点的下标是parent * 2 + 2，比如上图中的26 下标是1，1 * 2 + 1是下标为3的左孩子36。
下面是通过孩子访问父亲：
定义孩子下标为child,如果child是左孩子，那么(child - 1) / 2就可以得到父节点的下标，如果child是右孩子的话，本来我们应该是(child - 2) / 2，因为如果减一除二的话可能会得到一个小数，比如(4 - 1) / 2 = 1.5,但这是我们数学上的算法，在C语言里，整数除法是向下取整的，因此结果还是1，不是1.5，所以无论是左右孩子我们都可以减一除二得到父节点的下标。

另外，堆分为大堆和小堆，大堆满足父节点的数不小于子节点，小堆满足父节点不大于子节点。

1.1 向下调整算法

要想构建一个堆，我们得先学习向下调整算法，假设我们现在有一个堆，左子树和右子树都是小堆，只有堆顶不满足小堆的性质，比如这棵树
详解数据结构中的堆,数据结构,算法,c语言
我们只需要把堆顶的数据调到合适的位置，它就是一个小堆了，我们可以这样做：先找出堆顶的左右孩子中小的那一个，再让它和堆顶数据比较，如果孩子小，就让它和父节点进行交换，比如这里的29是父节点，它的左右孩子是26和16，其中小的是16，然后16和29比，孩子小，就让16和29进行交换
详解数据结构中的堆,数据结构,算法,c语言
此时我们交换的是右孩子和父节点，左边没有动过，因此左边依然是小堆，我们只需要改右边就可以了，现在新的29是我们下一个要进行比较的父节点，找出它的左右孩子中小的那一个，当然这里只有左孩子20，比较得父节点大，再交换左孩子和父节点
详解数据结构中的堆,数据结构,算法,c语言
此时，我们已经成功得到了一个小堆。
下面是代码实现（建小堆，如果要建大堆改掉一些小于号就可以），参数中arr是要调整的数组，n是数组的大小，root是堆顶的下标

void AdjustDown(HDataType* arr, int n, int root)
{
	int parent = root;
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n && arr[child] < arr[child + 1]) //child + 1 < n 防止越界
		{
			child = child + 1;
		}
		//到这child下标是两个孩子中小的呢个的下标
		if (arr[parent] < arr[child])
		{
			swap(&arr[parent], &arr[child]);
		}
		else 
		{
			break;
		}
		parent = child;
		child = 2 * parent + 1;
	}
}

但这样调整只适合左子树和右子树都已经是堆的情况啊，那一般的情况又怎么办呢？
其实，一棵树的每个叶节点可以看做只有它自己的一个堆，因为只有自己，所以它已经满足堆的条件
详解数据结构中的堆,数据结构,算法,c语言
比如这里的52,11,35,15,73。
如果我们对29进行向下调整算法，算法就会把29调到合适的位置，使得这个堆变成小堆，调完之后我们再调27，又可以把这个堆调成小堆，接下来继续往回走，再调46，直到把所有父节点都调完，整个堆就变成了小堆。
因为我们是用数组维护的堆，所以上面这个遍历父节点的过程我们可以通过下标减1来遍历。那怎么找到第一个父节点29呢，前面我们提到了size是数组里有效数据的个数，所以最后一个数据的下标就是size - 1，（size - 1）/ 2就是最后一个父节点的下标。

下面是利用向下调整建堆的代码

	for (int i = (size -1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, size, i);
	}

我们构建堆一般是放在堆的初始化函数里面的，堆的初始化一般就是给你一个数组，把数组里面的元素弄成堆。
ph是我们堆的结构体指针，使用前记得先创建一个结构体变量，这里是把它的地址传进去，s是我们要修改成堆的数组，n是数组的大小

void HeapInit(Heap* ph, HDataType* s, int n)
{
	ph->arr = (HDataType*)malloc(sizeof(HDataType) * n);
	memcpy(ph->arr, s, sizeof(HDataType) * n);//把s里面的数据复制到我们的数组里面
	ph->capacity = ph->size = n;

	//构建堆
	for (int i = (n - 1) / 2; i >= 0; i--)
	{
		AdjustDown(ph->arr, n, i);
	}
}

1.2 构建堆的时间复杂度分析

分析建堆的时间复杂度就是看它运行了多少次，向下调整算法每次需要移动树的高度-1次，设高度为h
详解数据结构中的堆,数据结构,算法,c语言建堆的时间复杂度就是每一层的节点个数乘以移动的次数，再把每一层相加，设和为S，即

求这个和我们用到错位相减法
详解数据结构中的堆,数据结构,算法,c语言同时，h = logN（默认以2为底），所以时间复杂度为O(N - logN)，因为logN很小，所以也就是O(N)。

2.堆排序

2.1 堆排序的实现

堆排序就是用堆这个数据结构来对一些数据进行排序，如果我们有一个小堆，那么堆顶的数就是最小的数，我们需要再找一个次小的数，该怎么找呢？
我们可以这样做：把堆顶的数和数组中最后一个数互换，然后把数组长度减1，认为最后一个数不是数组里面的，这样再对新的堆顶进行向下调整构建新的堆，这个时候的堆顶就是次小的数，再重复之前的操作，直到数组里只有一个数据，这个时候数组里面的数据就排好序了。
需要注意，这种排序 建大堆排升序，建小堆排降序。
代码实现：

void HeapSort(HDataType* arr,int n)
{
	//构建堆
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		AdjustDown(arr, n, i);
	}
	//开始排序
	int end = n - 1;   //数组最后一个数的下标
	while (end > 0)
	{
		swap(&arr[0], &arr[end]);
		AdjustDown(arr, end, 0);
		end--;
	}
}

2.2 堆排序的时间复杂度

堆排序的执行次数是数据个数乘以向下调整的时间复杂度，即
O(N * logN)，就算加上建堆的时间复杂度O(N),N 和 N * logN相比，N也比较小，所以直接取O(N * logN)。

3. TOP-K问题

这类问题是给出N个数，求出最小（最大）的前K个数，或者是第K小（大）的数。
这中问题用堆可以很好地解决，我们用N个数中的前K个数构建一个大小为K的堆，如果要最大的前K个数，就建小堆，然后再让堆顶的数和剩下的N-K个数一一比较，如果堆顶的数小，就把堆顶的数换成大的，再继续比较，最终堆里面的K个数就是最大的前K个数。
这种方法优点是可以解决数据太多内存放不下的问题，同时时间复杂度很小，为O(N*logK)。文章来源地址https://www.toymoban.com/news/detail-827888.html

到了这里，关于详解数据结构中的堆的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！