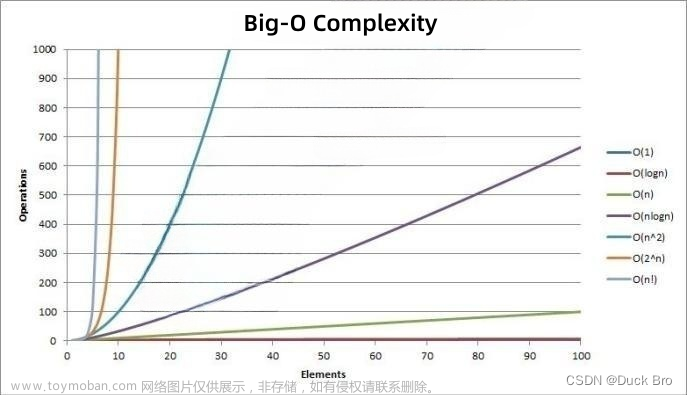
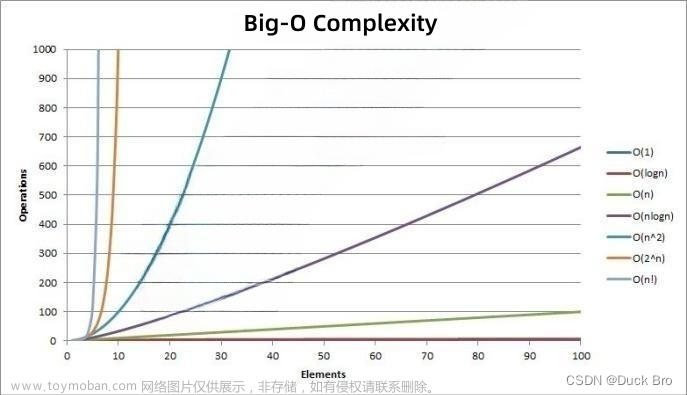
复杂度是我们学习数据结构的第一节,下面是我对该知识内容的一些理解。
1.什么是数据结构
概念:数据结构是计算机存储、组织数据的方式,指互相之间存在的一种或多种特定关系的数据元素的集合。
在实现一些项目时,需要在内存中将数据存储起来,存储需要各种方式,这些方式就被称作数据结构,我们学习数据结构就是要懂用哪种方式存储更加合适。
2.什么是算法
概念:定义良好的计算过程,他取一个或一组的值为输入,并产生一个或一组值为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化为输出结果。就如购物,我们经常通常会用到排序,如以价格排序等等,这里的排序就是一种算法。
那么如何衡量一个算法的好坏,就要引出我们的学习内容——算法的时间复杂度和空间复杂度
3.算法的复杂度
算法在编写可执行程序后,运行是需要耗费时间资源和空间资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。经过计算机行业的迅速发展,根据摩尔定律,计算机的存储容量已经达到很高的程度。(摩尔定律是指IC上可容纳的晶体管数目,约每隔18个月便会增加一倍,性能也将提升一倍。)
3.1 时间复杂度
概念:在计算机科学中,算法的时间复杂度是一个函数,他描述了算法的运行时间,但不同性能的计算机他的运行时间不能比较,所以有了时间复杂度这个分析方式,一个算法的所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
举例1:

该例写成函数为:F(N)=N^2+2*N+10
N无穷大时,N^2远远大于其他几位,实际中我们计算时间复杂度,不一定要计算到精确的次数,只需要大概的执行次数,那么这里我们用大O的渐进表示法。
3.2 大O的渐进表示法
1.用常数1取代运行时间中的所有加法常数。
2.在修改后的运行次数函数中,只保留最高项阶。
3.如果最高阶项存在且不是1,则去除与这个项目相乘的常数,得到的结果就是大O阶。
该例使用大O的渐进表示时间复杂度为: O(N^2)
在实际中一般情况关注的是算法的最坏运行情况
举例2:
strchr函数是C语言中的一个字符串处理函数,主要用于在一个字符串中查找指定字符的首次出现位置。如果找到该字符,则返回指向该字符的指针;如果没有找到,则返回NULL。这个函数在很多程序中都非常有用,特别是在需要对字符串进行逐字符处理的情况下。
在该例中,我们就该用最坏运行情况
举例3:冒泡排序

该算法我们光从代码中很难看出执行次数,因此我们需要通过代码的思想来计算次数。
在冒泡排序中,第一趟执行了N-1次,第二趟执行N-2次...,不难看出这是一个等差数列
故精确的执行次数为:F(N)=N*(N-1)/2 O(N)=N^2
举例4:

假设要查找X次,我们找一次数组中的数字少一半,最坏的情况就是左边的数等于右边的数,数组中只有一个数,在这种情况下,我们找一次数组中的元素就要除2,反过来推就是1*2*2*2*...=N,我们执行了多少次就要乘多少个2,故2^X=N,X=log2N
举例5:

递归算法的次数=递归次数*每次递归调用的次数
递归了N次,时间复杂度为O(N)
举例6:(通过画图分析)


Fib(N)=2^1+2^2+2^3+....+2^(N-1)-X=2^N-1-X
O(N)=2^N
等比数列求和公式:
4.空间复杂度
空间复杂度也是一个数学函数表达式,是对一个算法在运行过程中临时额外占用存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度计算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使大O渐进表示法
注意:(递归算法)函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
举例1:
在进行这个算法时定义的额外变量,在第一个i完成循环后空间会被销毁,第二个i和他用的是同一块空间,所以循环只额外使用了两个空间,故空间复杂度为:O(1)
(空间可以重复利用,不累计)
举例2:

栈的空间不大,如果是2^N,空间不够。空间是可以重复利用不累计的,时间是一去不复返,累积的。竖着先调用一遍,然后返回时销毁,在进行第二个调用。右边调用和左边的调用重复用了同一片空间,故空间复杂度:O(N)文章来源:https://www.toymoban.com/news/detail-828725.html
每次调用都要建立栈帧,再算到最后一个时返回才会销毁额外建立的栈帧,要看递归的深度。文章来源地址https://www.toymoban.com/news/detail-828725.html
到了这里,关于数据结构——复杂度讲解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!