目录
一.灰色关联度简介
二.灰色关联度
灰色关联分析案例
三.灰色预测模型简介
四.灰色预测之灰色生成数列
累加生成
累减生成
加权邻值生成
五.灰色模型GM（1，1）
GM（1，1）灰色预测的步骤
1.数据的检验与处理
2.建立GM（1，1）模型
3. 检验预测值
六.灰色预测案例
一.灰色关联度简介
灰色关联度是分析向量与向量之间或者矩阵与矩阵之间的关联度。既然计算关联度，就一定要有待比较数列和参照数列的关联度
二.灰色关联度
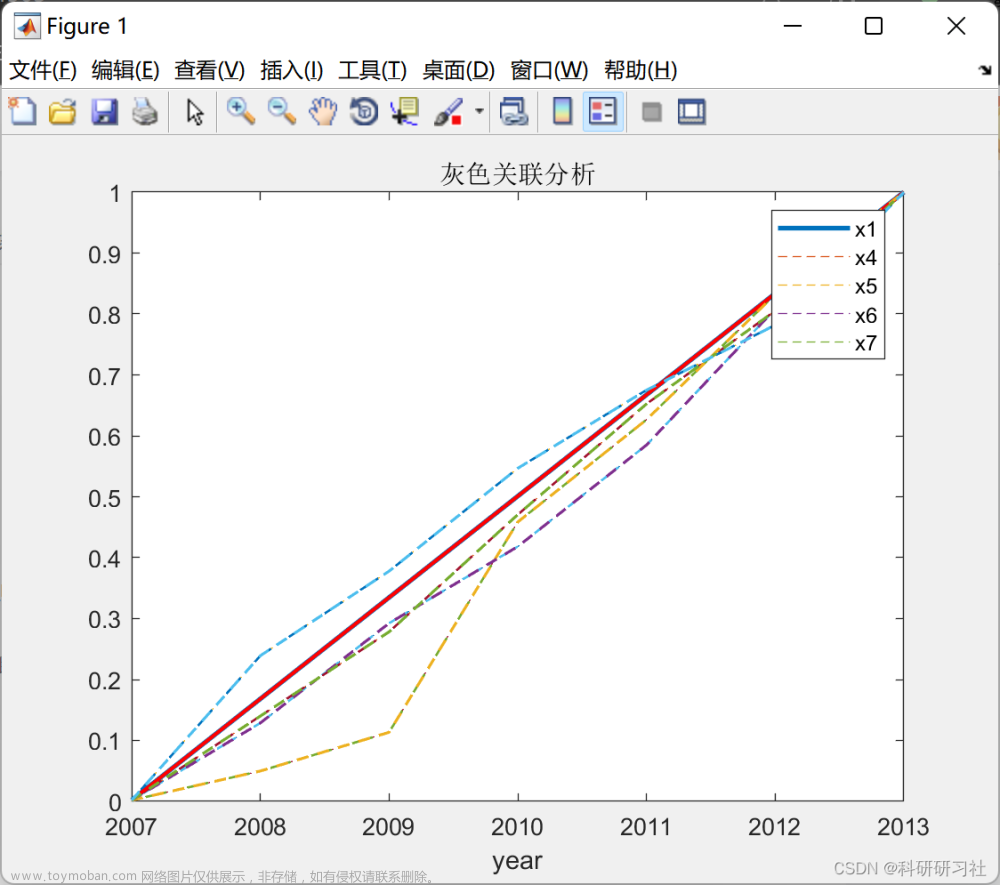
灰色关联分析案例
第一位老师工作最好
三.灰色预测模型简介
灰色预测模型 （ Gray Forecast Model ）是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。当我们应用运筹学的思想方法解决实际问题，制定发展战略和政策、进行重大问题的决策时，都必须对未来进行科学的预测 。预测是根据客观事物的过去和现在的发展规律，借助于科学的方法对其未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。
灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论。灰色预测是对灰色系统所做的预测。目前常用的一些预测方法（如回归分析等），需要较大的样本，若样本较小，常造成较大误差，使预测目标失效。灰色预测模型所需建模信息少，运算方便，建模精度高，在各种预测领域都有着广泛的应用，是处理小样本预测问题的有效工具。特别是它对时间序列短、统计数据少、信息不完全系统的分析与建模，具有独特的功效，因此得到了广泛的应用。
灰色系统是黑箱概念的一种推广。我们把既含有已知信息又含有未知信息的系统称为灰色系统作为两个极端，我们将称信息完全未确定的系统为黑色系统；称信息完全确定的系统为白色系统. 区别白色系统与黑色系统的重要标志是系统各因素之间是否具有确定的关系。
灰色预测模型使用范围：
①数据样本点个数少，6-15个
②数据呈现指数或曲线的形式
③只适合做中短期预测，不适合长期预测。
四.灰色预测之灰色生成数列
灰色系统理论认为，尽管客观表象复杂，但总是有整体功能的，因此必然蕴含某种内在规律。关键
在于如何选择适当的方式去挖掘和利用它。灰色系统是通过对原始数据的整理来寻求其变化规律的，这是一种就数据寻求数据的现实规律的途径，即为灰色序列的生成。一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。数据生成的常用方式有累加生成、累减生成和加权累加生成。
累加生成
比如数列（x1,x2,x3,x4),一次累加就是（x1,x2+x1,x3+x2+x1,……），就是前缀和数列
一般经济数列都是非负数列。累加生成能使任意非负数列、摆动的与非摆动的，转化为非减
的、递增的。
累减生成
比如数列（x1,x2,x3,x4),一次累减就是（x1,x2-x1,x3-x2,……）就是差分数列
可以把 积分与微分 类比 前缀和与拆分
加权邻值生成
五.灰色模型GM（1，1）
灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程，进而用离散数据列建立微分方程形式的动态模型，即灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起的微分方程形式的模型，这样便于对其变化过程进行研究和描述。
G表示grey（灰色），M表示model（模型）
为什么叫灰微分方程呢，因为它是离散的，不连续
GM（1，1）灰色预测的步骤
1.数据的检验与处理
2.建立GM（1，1）模型
3. 检验预测值
六.灰色预测案例
文章来源地址https://www.toymoban.com/news/detail-828826.html文章来源：https://www.toymoban.com/news/detail-828826.html
到了这里，关于【数学建模-灰色关联分析与灰色预测】的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
