「算法」二分查找1：理论&细节-Toy模板网

这篇具有很好参考价值的文章主要介绍了「算法」二分查找1：理论&细节。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🎇个人主页：Ice_Sugar_7
🎇所属专栏：算法详解
🎇欢迎点赞收藏加关注哦！

二分查找算法简介

这个算法的特点就是：细节多，出错率高，很容易就写成死循环
有模板，但切记要在理解的基础上记忆，不要死记硬背。有三个模板，一个是本文要讲的简单模板，另外两个分别是查找左、右边界的模板，会在后面的文章中讲解

正文

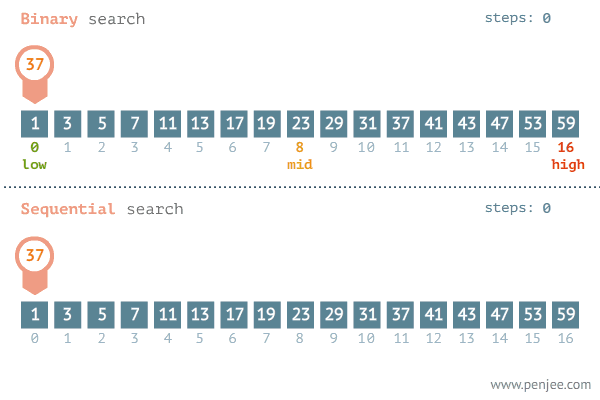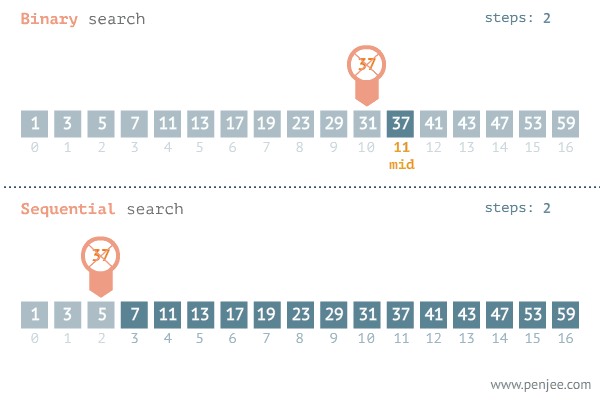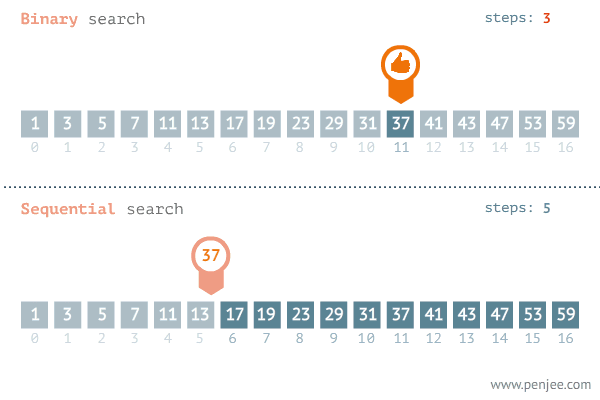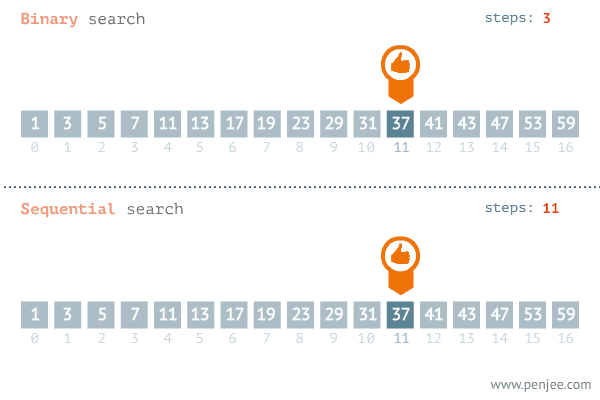
时间复杂度的推导过程
「算法」二分查找1：理论&细节,算法详解,算法,数据结构

啥时候用二分算法？

能找到某种规律，根据这个规律能找到某个点，以这个点能把区间划分为两块，其中一半区间可以舍弃掉，只需从另一半区间中继续查找

这么说肯定会觉得抽象，没事儿，后面做题慢慢体会
不过现在需要知道：不一定要数据有序才能用二分查找，只要能以某个点将区间分成两段就可以了（简称为“二段性”）

细节

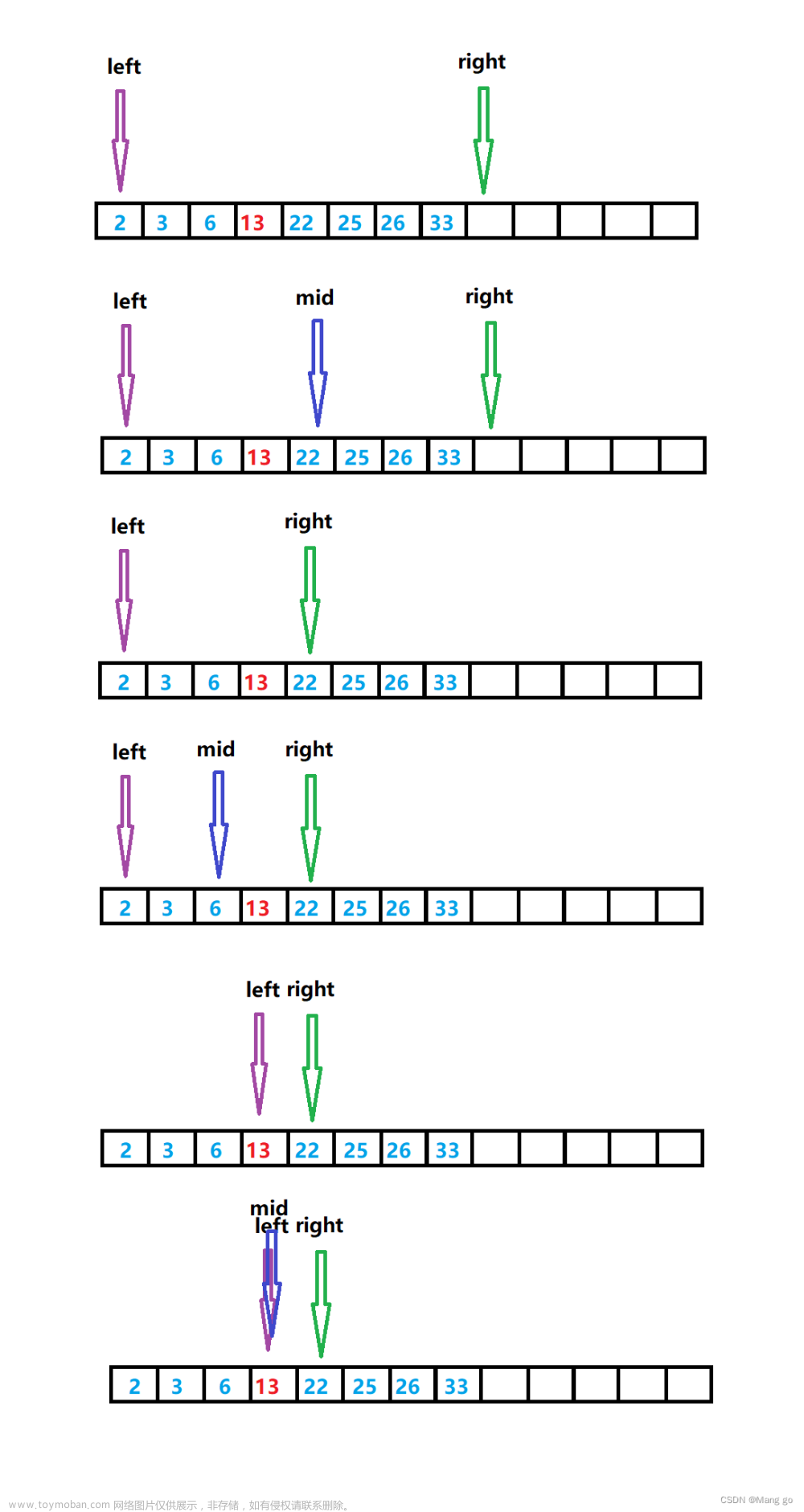
循环结束的条件

一开始定义两个指针 left 和 right ，分别指向数组的起始位置和最后一个位置
在每次循环中，我们只比较区间中点值 mid 和目标值 target 的大小关系，只知道这两个值，区间中剩下的值是啥仍然未知
即使这个区间只剩下一个数，也还是不知道它是谁，此时需要拿它和 target 作比较

所以，当 left > right 时，循环才结束

找区间的中点

由数学知识可得 mid = （left + right）/ 2
但是如果 left 和 right 很大的话，很可能会溢出，所以比较稳妥的写法是 mid = left + （right - left）/ 2，即左端点加上区间长度的一半

如果一共有奇数个元素，那么 mid 就是正中间那个；如果有偶数个，那就有两个中点，上面那两个式子算出来的是靠左边的中点

而如果要找靠右边的中点，只需加个1：mid = （left + right + 1）/ 2 和 mid = left + （right - left + 1）/ 2

简单的二分查找模板

来道简单题，它的答案就是模板：
二分查找

class Solution {
    public int search(int[] nums, int target) {
        int left = 0,right = nums.length-1;
        while(left <= right) {
            int mid = left+(right-left)/2;
            if(nums[mid] < target) left = mid+1;
            else if(nums[mid] > target) right = mid - 1;
            else return mid;
        }
        return -1;
    }
}

模板为：

public int search(int[] nums, int target) {
        int left = 0,right = nums.length-1;
        while(left <= right) {
            int mid = left+(right-left)/2;
            if(...) left = mid+1;
            else if(...) right = mid - 1;
            else return ...;
        }
        return -1;
    }